4.5: F-Test for Comparing Two Population Variances
- Page ID
- 2894
F-Test for Comparing Two Population Variances
One major application of a test for the equality of two population variances is for checking the validity of the equal variance assumption \((\sigma_1^2=\sigma_2^2)\) for a two-sample t-test. First we hypothesize two populations of measurements that are normally distributed. We label these populations as 1 and 2, respectively. We are interested in comparing the variance of population 1 \((\sigma_1^2)\) to the variance of population 2 \((\sigma_2^2)\).
When independent random samples have been drawn from the respective populations, the ratio
\[\frac {S^2_1/S_2^2}{\sigma_1^2/\sigma ^2_2}\]
possesses a probability distribution in repeated sampling that is referred to as an F distribution and its properties are:
- Unlike Z and t, but like \(\chi^2\), F can assume only positive values.
- The F distribution, unlike the Z and t distributions, but like the (\chi^2\) distribution, is non-symmetrical.
- There are many F distributions, and each one has a different shape. We specify a particular one by designating the degrees of freedom associated with \(S_1^2\) and \(S_2^2\). We denote these quantities by \(df_1\) and \(df_2\), respectively.
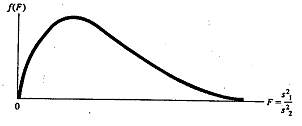
Figure \(\PageIndex{1}\): The F-distribution.
Note: A statistical test of the null hypothesis \(\sigma_1^2 = \sigma_2^2\) utilizes the test statistic \(S_1^2/S_2^2\). It may require either upper tail or lower tail rejection region, depending on which sample variance is larger. To alleviate this situation, we are at liberty to designate the population with the larger sample variance as population 1 (i.e., used as the numerator of the ratio \(S_1^2/S_2^2\)). By this convention, the rejection region is only located in the upper tail of the F distribution.
Null hypothesis: \(H_0:\sigma_1^2 = \sigma_2^2\)
Alternative hypothesis:
- \(H_a: \sigma_1^2 > \sigma_2^2\) (one-tailed), reject \(H_0\) if the observed F > Fα
- \(H_a: \sigma_1^2 \ne \sigma_2^2\) (two-tailed), reject \(H_0\) if the observed F > Fα/2.
Test statistic: \(F = \frac {S_1^2}{S^2_2}\) assuming \(S_1^2>S_2^2\),
where the F critical value in the rejection region is based on 2 degrees of freedom \(df_1 = n_1 – 1\) (associated with numerator \(S_1^2\)) and \(df_2 = n_2 – 1\) (associated with denominator \(S_2^2\)).
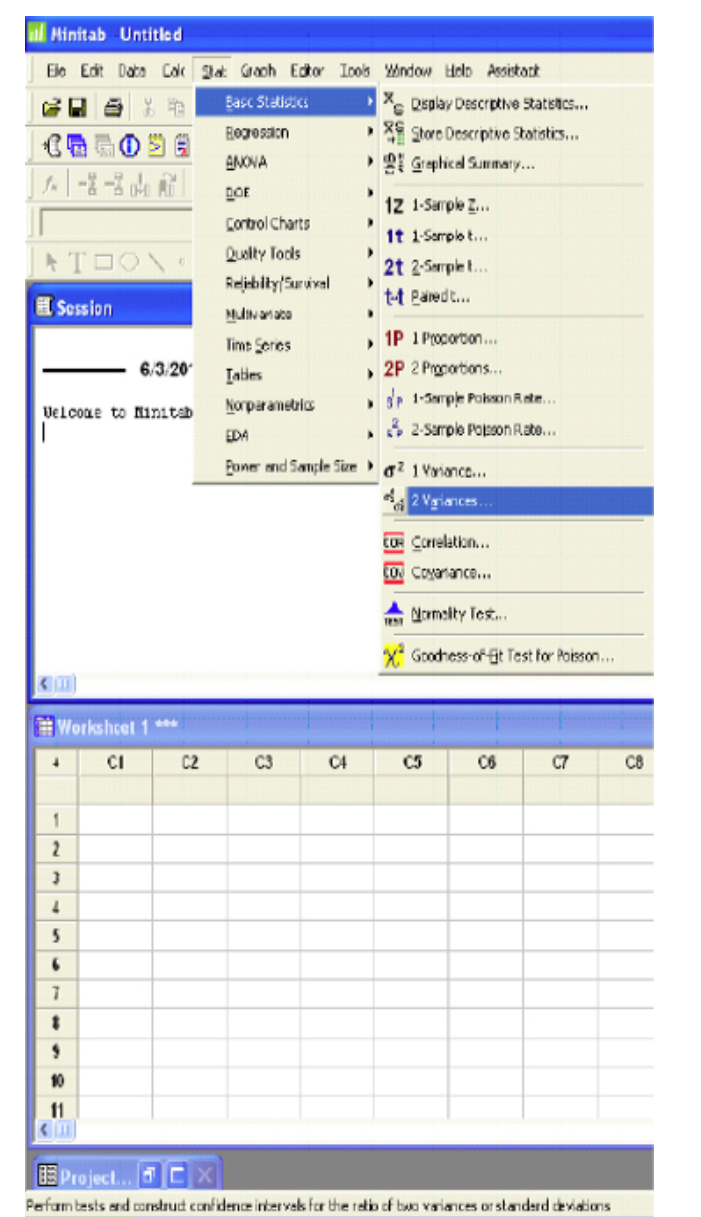
A forester wants to compare two different mist blowers for consistent application. She wants to use the mist blower with the smaller variance, which means more consistent application. She wants to test that the variance of Type A (0.087 gal.2) is significantly greater than the variance of Type B (0.073 gal.2) using α = 0.05.
| Type A | Type B |
| \(S_1^2\) = 0.087 | \(S^2_2\)=0.073 |
| \(n_1\)= 16 | \(n_2\) = 21 |
Solution
\(H_0: \sigma_1^2 = \sigma_2^2\)
\(H_1:\sigma_1^2 > \sigma_2^2\)
The critical value \((df_1 = 15\) and \(df_2 = 20)\) is 2.20.
The test statistic is:
\[F = \frac {S_1^2}{S_2^2} = \frac {0.087}{0.073}=1.192\]
The test statistic is not larger than the critical value (it does not fall in the rejection zone) so we fail to reject the null hypothesis. While the variance of Type B is mathematically smaller than the variance of Type A, it is not statistically smaller. There is not enough statistical evidence to support the claim that the variance of Type A is significantly greater than the variance of Type B. Both mist blowers will deliver the chemical with equal consistency.
Software Solutions
Minitab
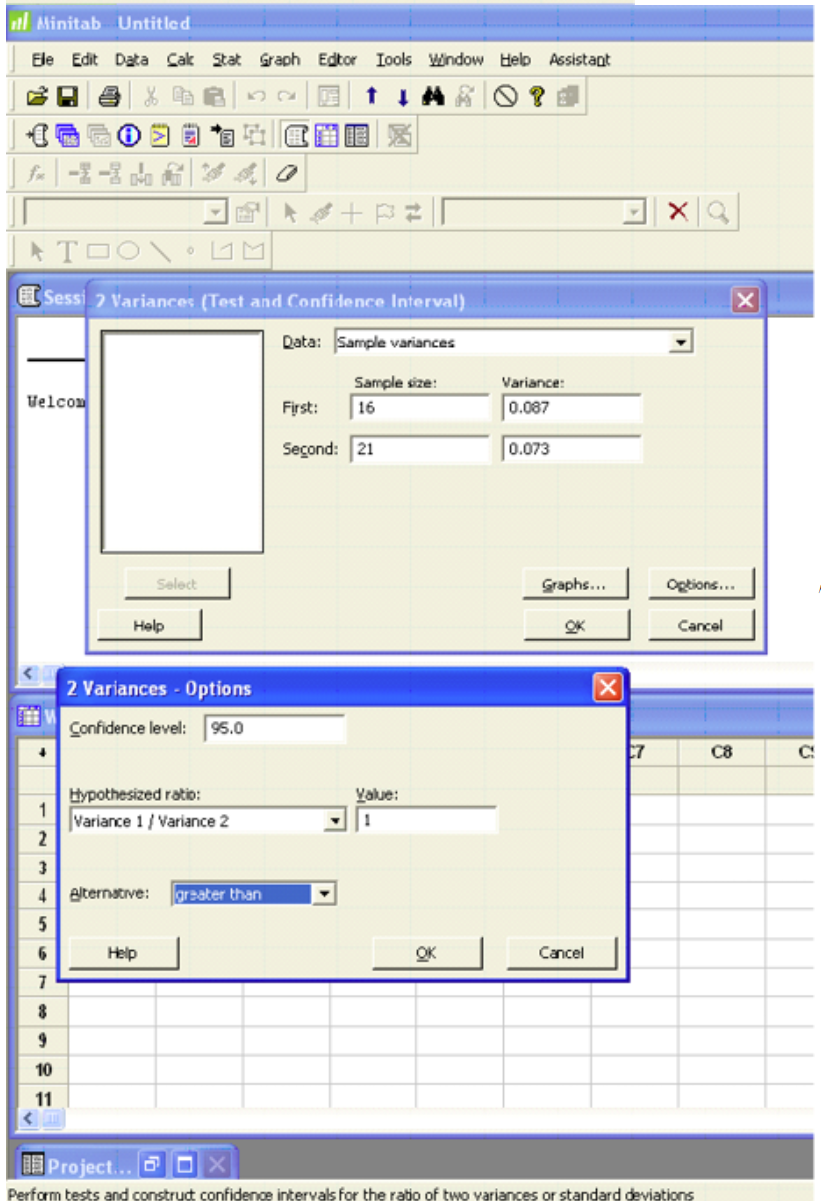
Test and CI for Two Variances - Methods
|
Null hypothesis |
Variance(1) / Variance(2) = 1 |
||||
|---|---|---|---|---|---|
|
Alternative hypothesis |
Variance(1) / Variance(2) > 1 |
||||
|
Significance level |
Alpha = 0.05 |
||||
|
Statistics |
|||||
|
Sample |
N |
StDev |
Variance |
||
|
1 |
16 |
0.295 |
0.087 |
||
|
2 |
21 |
0.270 |
0.073 |
||
|
Ratio of standard deviations = 1.092 |
|||||
|
Ratio of variances = 1.192 |
|||||
|
Tests |
|||||
|
Test |
|||||
|
Method |
DF1 |
DF2 |
Statistic |
p-value |
|
|
F Test (normal) |
15 |
20 |
1.19 |
0.351 |
|
Excel
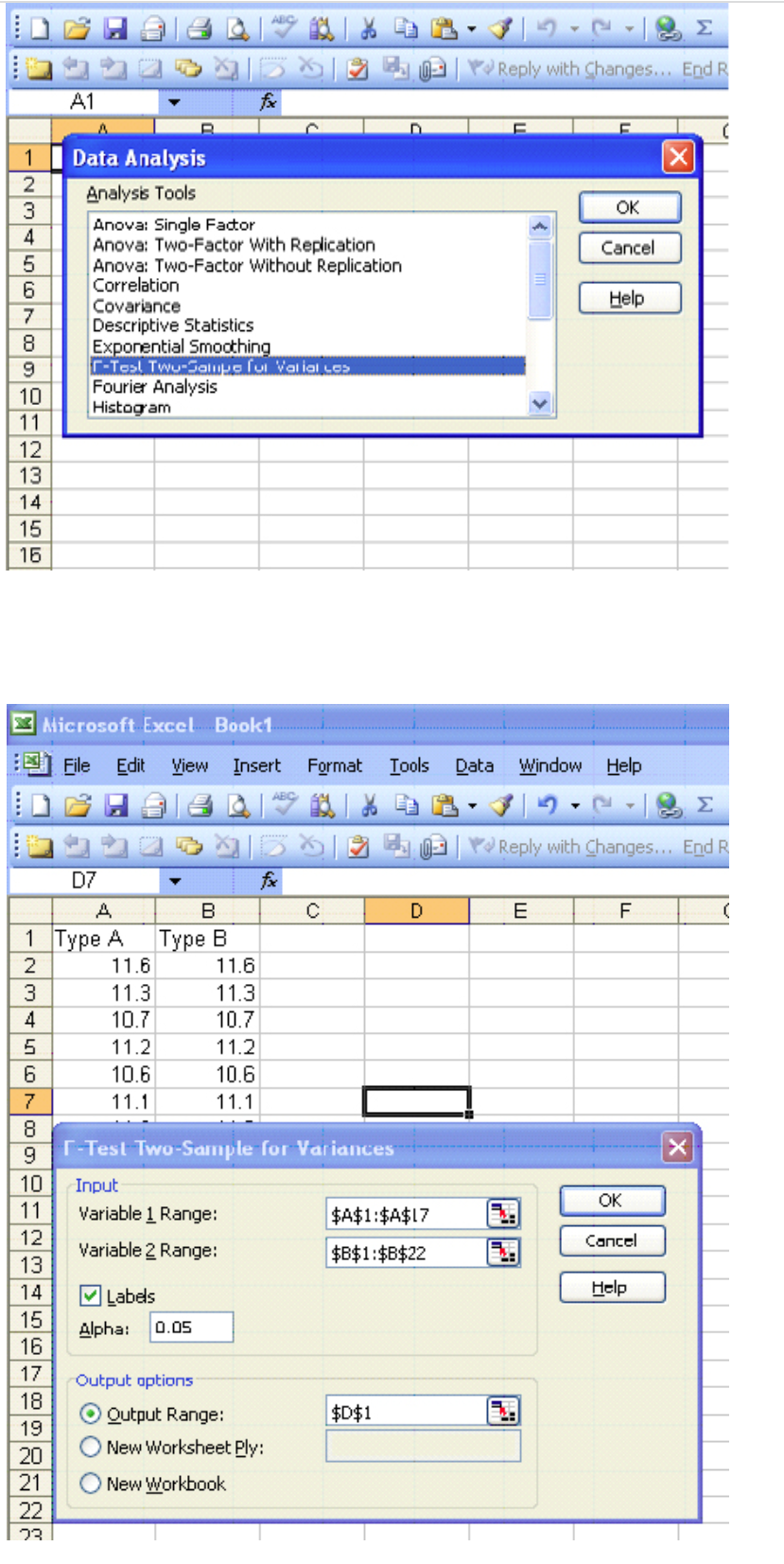
F-Test Two-Sample for Variances
|
Type A |
Type B |
|
|---|---|---|
|
Mean |
11.07188 |
11.10595 |
|
Variance |
0.08699 |
0.073379 |
|
Observations |
16 |
21 |
|
df |
15 |
20 |
|
F |
1.185483 |
|
|
\(P(F\le f)\) one-tail |
0.355098 |
|
|
F Critical one-tail |
2.203274 |


