3.1: Statistics of Central Tendency

Last updated
Save as PDF

Page ID: 1729

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

A statistic of central tendency tells you where the middle of a set of measurements is. The arithmetic mean is by far the most common, but the median, geometric mean, and harmonic mean are sometimes useful.

Introduction

All of the tests in the first part of this handbook have analyzed nominal variables. You summarize data from a nominal variable as a percentage or a proportion. For example, $76.1\%$ (or $0.761$) of the peas in one of Mendel's genetic crosses were smooth, and $23.9\%$ were wrinkled. If you have the percentage and the sample size ($556$, for Mendel's peas), you have all the information you need about the variable.

The rest of the tests in this handbook analyze measurement variables. Summarizing data from a measurement variable is more complicated, and requires a number that represents the "middle" of a set of numbers (known as a "statistic of central tendency" or "statistic of location"), along with a measure of the "spread" of the numbers (known as a "statistic of dispersion"). The arithmetic mean is the most common statistic of central tendency, while the variance or standard deviation are usually used to describe the dispersion.

The statistical tests for measurement variables assume that the probability distribution of the observations fits the normal (bell-shaped) curve. If this is true, the distribution can be accurately described by two parameters, the arithmetic mean and the variance. Because they assume that the distribution of the variables can be described by these two parameters, tests for measurement variables are called "parametric tests." If the distribution of a variable doesn't fit the normal curve, it can't be accurately described by just these two parameters, and the results of a parametric test may be inaccurate. In that case, the data can be converted to ranks and analyzed using a non-parametric test, which is less sensitive to deviations from normality.

The Normal Distribution

Many measurement variables in biology fit the normal distribution fairly well. According to the central limit theorem, if you have several different variables that each have some distribution of values and add them together, the sum follows the normal distribution fairly well. It doesn't matter what the shape of the distribution of the individual variables is, the sum will still be normal. The distribution of the sum fits the normal distribution more closely as the number of variables increases. The graphs below are frequency histograms of $5,000$ numbers. The first graph shows the distribution of a single number with a uniform distribution between $0$ and $1$. The other graphs show the distributions of the sums of two, three, or four random numbers with the same distribution.

Fig. 3.1.1 Histograms of sums of random numbers.

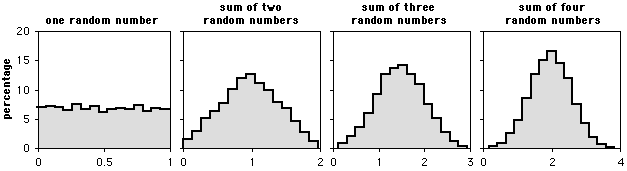
As you can see, as more random numbers are added together, the frequency distribution of the sum quickly approaches a bell-shaped curve. This is analogous to a biological variable that is the result of several different factors. For example, let's say that you've captured $100$ lizards and measured their maximum running speed. The running speed of an individual lizard would be a function of its genotype at many genes; its nutrition as it was growing up; the diseases it's had; how full its stomach is now; how much water it's drunk; and how motivated it is to run fast on a lizard racetrack. Each of these variables might not be normally distributed; the effect of disease might be to either subtract $10\; cm/sec$ if it has had lizard-slowing disease, or add $20\; cm/sec$ if it has not; the effect of gene A might be to add $25\; cm/sec$ for genotype $AA$, $20\; cm/sec$ for genotype $Aa$, or $15\; cm/sec$ for genotype $aa$. Even though the individual variables might not have normally distributed effects, the running speed that is the sum of all the effects would be normally distributed.

If the different factors interact in a multiplicative, not additive, way, the distribution will be log-normal. An example would be if the effect of lizard-slowing disease is not to subtract $10\; cm/sec$ from the average speed, but instead to reduce the speed by $10\%$ (in other words, multiply the speed by $0.9$). The distribution of a log-normal variable will look like a bell curve that has been pushed to the left, with a long tail going to the right. Taking the log of such a variable will produce a normal distribution. This is why the log transformation is used so often.

Fig. 3.1.2 Histograms of the product of four random numbers, without or with log transformation.

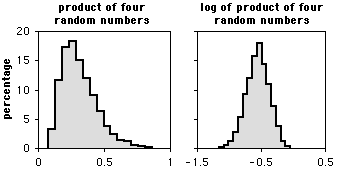
The figure above shows the frequency distribution for the product of four numbers, with each number having a uniform random distribution between $0.5$ and $1$. The graph on the left shows the untransformed product; the graph on the right is the distribution of the log-transformed products.

Different measures of central tendency

While the arithmetic mean is by far the most commonly used statistic of central tendency, you should be aware of a few others.

Arithmetic mean

The arithmetic mean is the sum of the observations divided by the number of observations. It is the most common statistic of central tendency, and when someone says simply "the mean" or "the average," this is what they mean. It is often symbolized by putting a bar over a letter; the mean of $Y_1,\; Y_2,\; Y_3,...$ is $Y$.

The arithmetic mean works well for values that fit the normal distribution. It is sensitive to extreme values, which makes it not work well for data that are highly skewed. For example, imagine that you are measuring the heights of fir trees in an area where $99\%$ of trees are young trees, about $1$ meter tall, that grew after a fire, and $1\%$ of the trees are $50$-meter-tall trees that survived the fire. If a sample of $20$ trees happened to include one of the giants, the arithmetic mean height would be $3.45$ meters; a sample that didn't include a big tree would have a mean height of about $1$ meter. The mean of a sample would vary a lot, depending on whether or not it happened to include a big tree.

In a spreadsheet, the arithmetic mean is given by the function AVERAGE(Ys), where $Ys$ represents a listing of cells ($A2,\; B7,\; B9$) or a range of cells ($A2:A20$) or both ($A2,\; B7,\; B9:B21$). Note that spreadsheets only count those cells that have numbers in them; you could enter AVERAGE($A1:A100$), put numbers in cells $A1\; to\; A9$, and the spreadsheet would correctly compute the arithmetic mean of those $9$ numbers. This is true for other functions that operate on a range of cells.

Geometric mean

The geometric mean is the $N^{th}$ root of the product of $N$ values of $Y$; for example, the geometric mean of $5$ values of $Y$ would be the $5^{th}$ root of $Y_1\times Y_2\times Y_3\times Y_4\times Y_5$. It is given by the spreadsheet function GEOMEAN($Ys$). The geometric mean is used for variables whose effect is multiplicative. For example, if a tree increases its height by $60\%$ one year, $8\%$ the next year, and $4\%$ the third year, its final height would be the initial height multiplied by $1.60\times 1.08\times 1.04=1.80$. Taking the geometric mean of these numbers ($1.216$) and multiplying that by itself three times also gives the correct final height ($1.80$), while taking the arithmetic mean ($1.24$) times itself three times does not give the correct final height. The geometric mean is slightly smaller than the arithmetic mean; unless the data are highly skewed, the difference between the arithmetic and geometric means is small.

If any of your values are zero or negative, the geometric mean will be undefined.

The geometric mean has some useful applications in economics involving interest rates, etc., but it is rarely used in biology. You should be aware that it exists, but I see no point in memorizing the definition.

Harmonic mean

The harmonic mean is the reciprocal of the arithmetic mean of reciprocals of the values; for example, the harmonic mean of $5$ values of $Y$ would be $\frac{5}{1/Y_1+1/Y_2+1/Y_3+1/Y_4+1/Y_5}$. It is given by the spreadsheet function HARMEAN($Ys$). The harmonic mean is less sensitive to a few large values than are the arithmetic or geometric mean, so it is sometimes used for highly skewed variables such as dispersal distance. For example, if six birds set up their first nest $1.0,\; 1.4,\; 1.7,\; 2.1,\; 2.8,\; and\; 47\; km$ from the nest they were born in, the arithmetic mean dispersal distance would be $9.33\; km$, the geometric mean would be $2.95\; km$, and the harmonic mean would be $1.90\; km$.

If any of your values are zero, the harmonic mean will be undefined.

I think the harmonic mean has some useful applications in engineering, but it is rarely used in biology. You should be aware that it exists, but I see no point in memorizing the definition.

Median

When the $Ys$ are sorted from lowest to highest, this is the value of $Y$ that is in the middle. For an odd number of $Ys$, the median is the single value of $Y$ in the middle of the sorted list; for an even number, it is the arithmetic mean of the two values of $Y$ in the middle. Thus for a sorted list of $5$ $Ys$, the median would be $Y_3$; for a sorted list of $6$ $Y$s, the median would be the arithmetic mean of $Y_3$ and $Y_4$. The median is given by the spreadsheet function MEDIAN(Ys).

The median is useful when you are dealing with highly skewed distributions. For example, if you were studying acorn dispersal, you might find that the vast majority of acorns fall within $5$ meters of the tree, while a small number are carried $500$ meters away by birds. The arithmetic mean of the dispersal distances would be greatly inflated by the small number of long-distance acorns. It would depend on the biological question you were interested in, but for some purposes a median dispersal distance of $3.5$ meters might be a more useful statistic than a mean dispersal distance of $50$ meters.

The second situation where the median is useful is when it is impractical to measure all of the values, such as when you are measuring the time until something happens. Survival time is a good example of this; in order to determine the mean survival time, you have to wait until every individual is dead, while determining the median survival time only requires waiting until half the individuals are dead.

There are statistical tests for medians, such as Mood's median test, but not many people use them because of their lack of power, and I don't discuss them in this handbook. If you are working with survival times of long-lived organisms (such as people), you'll need to learn about the specialized statistics for that; Bewick et al. (2004) is one place to start.

Mode

This is the most common value in a data set. It requires that a continuous variable be grouped into a relatively small number of classes, either by making imprecise measurements or by grouping the data into classes. For example, if the heights of $25$ people were measured to the nearest millimeter, there would likely be $25$ different values and thus no mode. If the heights were measured to the nearest $5$ centimeters, or if the original precise measurements were grouped into $5$-centimeter classes, there would probably be one height that several people shared, and that would be the mode.

It is rarely useful to determine the mode of a set of observations, but it is useful to distinguish between unimodal, bimodal, etc. distributions, where it appears that the parametric frequency distribution underlying a set of observations has one peak, two peaks, etc. The mode is given by the spreadsheet function MODE(Ys).

Example

Fig. 3.1.3 The blacknose dace, Rhinichthys atratulus.

The Maryland Biological Stream Survey used electrofishing to count the number of individuals of each fish species in randomly selected $75m$ long segments of streams in Maryland. Here are the numbers of blacknose dace, Rhinichthys atratulus, in streams of the Rock Creek watershed:

Stream	fish/75m
Mill_Creek_1	76
Mill_Creek_2	102
North_Branch_Rock_Creek_1	12
North_Branch_Rock_Creek_2	39
Rock_Creek_1	55
Rock_Creek_2	93
Rock_Creek_3	98
Rock_Creek_4	53
Turkey_Branch	102

Here are the statistics of central tendency. In reality, you would rarely have any reason to report more than one of these:

Arithmetic mean	70.0
Geometric mean	59.8
Harmonic mean	45.1
Median	76
Mode	102

How to calculate the statistics

Spreadsheet

I have made a descriptive statistics spreadsheet descriptive.xls that calculates the arithmetic, geometric and harmonic means, the median, and the mode, for up to $1000$ observations.

Web pages

This web page calculates arithmetic mean and median for up to $10,000$ observations. It also calculates standard deviation, standard error of the mean, and confidence intervals.

R

Salvatore Mangiafico's $R$ Companion has sample R programs for mean, median and mode.

SAS

There are three SAS procedures that do descriptive statistics, PROC MEANS, PROC SUMMARY, and PROC UNIVARIATE. I don't know why there are three. PROC UNIVARIATE will calculate a longer list of statistics, so you might as well use it. Here is an example, using the fish data from above.

DATA fish;
INPUT location $ dacenumber;
DATALINES;
Mill_Creek_1 76
Mill_Creek_2 102
North_Branch_Rock_Creek_1 12
North_Branch_Rock_Creek_2 39
Rock_Creek_1 55
Rock_Creek_2 93
Rock_Creek_3 98
Rock_Creek_4 53
Turkey_Branch 102
;
PROC UNIVARIATE DATA=fish;
RUN;

There's a lot of output from PROC UNIVARIATE, including the arithmetic mean, median, and mode:

Basic Statistical Measures

Location Variability

Mean 70.0000 Std Deviation 32.08582
Median 76.0000 Variance 1030
Mode 102.0000 Range 90.00000
Interquartile Range 45.00000

You can specify which variables you want the mean, median and mode of, using a VAR statement. You can also get the statistics for just those values of the measurement variable that have a particular value of a nominal variable, using a CLASS statement. This example calculates the statistics for the length of mussels, separately for each of two species, Mytilus edulis and M. trossulus.

DATA mussels;
INPUT species $ length width;
DATALINES;
edulis 49.0 11.0
tross 51.2 9.1
tross 45.9 9.4
edulis 56.2 13.2
edulis 52.7 10.7
edulis 48.4 10.4
tross 47.6 9.5
tross 46.2 8.9
tross 37.2 7.1
;
PROC UNIVARIATE DATA=mussels;
VAR length;
CLASS species;
RUN;

Surprisingly, none of the SAS procedures calculate harmonic or geometric mean. There are functions called HARMEAN and GEOMEAN, but they only calculate the means for a list of variables, not all the values of a single variable.

References

Picture of blacknose dace from Ohio Division of Natural Areas and Preserves.

Blacknose dace data from Maryland Biological Stream Survey.

Bewick, V., L. Cheek, and J. Ball. 2004. Statistics review 12: Survival analysis. Critical Care 8: 389-394.

Search

Text Color

Text Size

Margin Size

Font Type

Learning Objectives

Example