4.3: Basic Probability Theory
- Page ID
- 7907
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ideological arguments between Bayesians and frequentists notwithstanding, it turns out that people mostly agree on the rules that probabilities should obey. There are lots of different ways of arriving at these rules. The most commonly used approach is based on the work of Andrey Kolmogorov, one of the great Soviet mathematicians of the 20th century. I won’t go into a lot of detail, but I’ll try to give you a bit of a sense of how it works. And in order to do so, I’m going to have to talk about my pants.
Introducing Probability Distributions
One of the disturbing truths about my life is that I only own 5 pairs of pants: three pairs of jeans, the bottom half of a suit, and a pair of tracksuit pants. Even sadder, I’ve given them names: I call them \(X_1\), \(X_2\), \(X_3\), \(X_4\) and \(X_5\). I really do: that’s why they call me Mister Imaginative. Now, on any given day, I pick out exactly one of pair of pants to wear. Not even I’m so stupid as to try to wear two pairs of pants, and thanks to years of training I never go outside without wearing pants anymore. If I were to describe this situation using the language of probability theory, I would refer to each pair of pants (i.e., each \(X\)) as an elementary event. The key characteristic of elementary events is that every time we make an observation (e.g., every time I put on a pair of pants), then the outcome will be one and only one of these events. Like I said, these days I always wear exactly one pair of pants, so my pants satisfy this constraint. Similarly, the set of all possible events is called a sample space. Granted, some people would call it a “wardrobe”, but that’s because they’re refusing to think about my pants in probabilistic terms. Sad.
Okay, now that we have a sample space (a wardrobe), which is built from lots of possible elementary events (pants), what we want to do is assign a probability of one of these elementary events. For an event \(X\), the probability of that event \(P(X)\) is a number that lies between 0 and 1. The bigger the value of \(P(X)\), the more likely the event is to occur. So, for example, if \(P(X) = 0\), it means the event \(X\) is impossible (i.e., I never wear those pants). On the other hand, if \(P(X) = 1\) it means that event \(X\) is certain to occur (i.e., I always wear those pants). For probability values in the middle, it means that I sometimes wear those pants. For instance, if \(P(X) = 0.5\) it means that I wear those pants half of the time.
At this point, we’re almost done. The last thing we need to recognise is that “something always happens”. Every time I put on pants, I really do end up wearing pants (crazy, right?). What this somewhat trite statement means, in probabilistic terms, is that the probabilities of the elementary events need to add up to 1. This is known as the law of total probability, not that any of us really care. More importantly, if these requirements are satisfied, then what we have is a probability distribution. For example, this is an example of a probability distribution
| Which pants? | Label | Probability |
|---|---|---|
| Blue jeans | \(X_1\) | \(P(X_1) = .5\) |
| Grey jeans | \(X_2\) | \(P(X_2) = .3\) |
| Black jeans | \(X_3\) | \(P(X_3) = .1\) |
| Black suit | \(X_4\) | \(P(X_4) = 0\) |
| Blue tracksuit | \(X_5\) | \(P(X_5) = .1\) |
Each of the events has a probability that lies between 0 and 1, and if we add up the probability of all events, they sum to 1. Awesome. We can even draw a nice bar graph to visualise this distribution, as shown in Figure \(\PageIndex{1}\). And at this point, we’ve all achieved something. You’ve learned what a probability distribution is, and I’ve finally managed to find a way to create a graph that focuses entirely on my pants. Everyone wins!
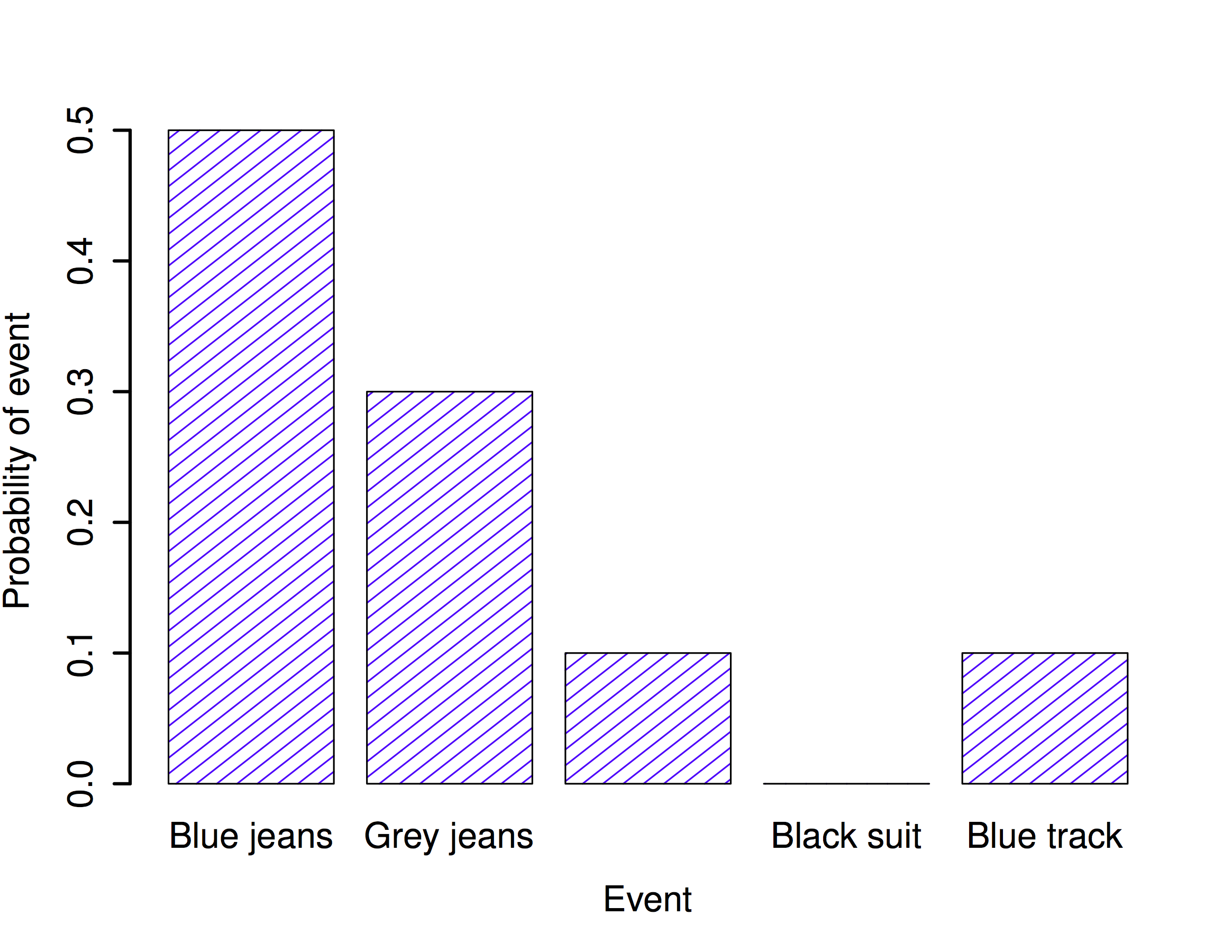
The only other thing that I need to point out is that probability theory allows you to talk about non elementary events as well as elementary ones. The easiest way to illustrate the concept is with an example. In the pants example, it’s perfectly legitimate to refer to the probability that I wear jeans. In this scenario, the “Dan wears jeans” event said to have happened as long as the elementary event that actually did occur is one of the appropriate ones; in this case “blue jeans”, “black jeans” or “grey jeans”. In mathematical terms, we defined the “jeans” event \(E\) to correspond to the set of elementary events \((X_1, X_2, X_3)\). If any of these elementary events occurs, then \(E\) is also said to have occurred. Having decided to write down the definition of the \(E\) this way, it’s pretty straightforward to state what the probability \(P(E)\) is: we just add everything up. In this particular case
\[P(E) = P(X_1) + P(X_2) + P(X_3) \nonumber \]
and, since the probabilities of blue, grey and black jeans respectively are .5, .3 and .1, the probability that I wear jeans is equal to .9.
At this point you might be thinking that this is all terribly obvious and simple and you’d be right. All we’ve really done is wrap some basic mathematics around a few common sense intuitions. However, from these simple beginnings it’s possible to construct some extremely powerful mathematical tools. I’m definitely not going to go into the details in this book, but what I will do is list some of the other rules that probabilities satisfy. These rules can be derived from the simple assumptions that I’ve outlined above, but since we don’t actually use these rules for anything in this book, I won’t do so here.
| English | Notation | Formula | |
|---|---|---|---|
| not \(A\) | \(P(\neg A)\) | \(=\) | \(1-P(A)\) |
| \(A\) or \(B\) | \(P(A \cup B)\) | \(=\) | \(P(A) + P(B) - P(A \cap B)\) |
| \(A\) and \(B\) | \(P(A \cap B)\) | \(=\) | \(P(A|B) P(B)\) |
Now that we have the ability to “define” non-elementary events in terms of elementary ones, we can actually use this to construct (or, if you want to be all mathematicallish, “derive”) some of the other rules of probability. These rules are listed above, and while I’m pretty confident that very few of my readers actually care about how these rules are constructed, I’m going to show you anyway: even though it’s boring and you’ll probably never have a lot of use for these derivations, if you read through it once or twice and try to see how it works, you’ll find that probability starts to feel a bit less mysterious, and with any luck a lot less daunting. So here goes. Firstly, in order to construct the rules I’m going to need a sample space \(X\) that consists of a bunch of elementary events \(x\), and two non-elementary events, which I’ll call \(A\) and \(B\). Let’s say:
\[\begin{array}{rcl} X &=& (x_1, x_2, x_3, x_4, x_5) \\ A &=& (x_1, x_2, x_3) \\ B &=& (x_3, x_4) \end{array} \nonumber \]
To make this a bit more concrete, let’s suppose that we’re still talking about the pants distribution. If so, \(A\) corresponds to the event “jeans”, and \(B\) corresponds to the event “black”:
\[\begin{array}{rcl} \mbox{"jeans''} &=& (\mbox{"blue jeans''}, \mbox{"grey jeans''}, \mbox{"black jeans''}) \\ \mbox{"black''} &=& (\mbox{"black jeans''}, \mbox{"black suit''}) \end{array} \nonumber \]
So now let’s start checking the rules that I’ve listed in the table.
In the first line, the table says that
\[P(\neg A) = 1- P(A) \nonumber \]
and what it means is that the probability of “not \(A\)” is equal to 1 minus the probability of \(A\). A moment’s thought (and a tedious example) make it obvious why this must be true. If \(A\) coresponds to the even that I wear jeans (i.e., one of \(x_1\) or \(x_2\) or \(x_3\) happens), then the only meaningful definition of “not \(A\)” (which is mathematically denoted as \(\neg A\)) is to say that \(\neg A\) consists of all elementary events that don’t belong to \(A\). In the case of the pants distribution it means that \(\neg A = (x_4, x_5)\), or, to say it in English: “not jeans” consists of all pairs of pants that aren’t jeans (i.e., the black suit and the blue tracksuit). Consequently, every single elementary event belongs to either \(A\) or \(\neg A\), but not both. Okay, so now let’s rearrange our statement above:
\[P(\neg A) + P(A) = 1 \nonumber \]
which is a trite way of saying either I do wear jeans or I don’t wear jeans: the probability of “not jeans” plus the probability of “jeans” is 1. Mathematically:
\[\begin{array}{rcl} P(\neg A) &=& P(x_4) + P(x_5) \\ P(A) &=& P(x_1) + P(x_2) + P(x_3) \end{array} \nonumber \]
so therefore
\[\begin{array}{rcl} P(\neg A) + P(A) &=& P(x_1) + P(x_2) + P(x_3) + P(x_4) + P(x_5) \\ &=& \sum_{x \in X} P(x) \\ &=& 1 \end{array} \nonumber \]
Excellent. It all seems to work.
Wow, I can hear you saying. That’s a lot of \(x\)s to tell me the freaking obvious. And you’re right: this is freaking obvious. The whole point of probability theory to to formalise and mathematise a few very basic common sense intuitions. So let’s carry this line of thought forward a bit further. In the last section I defined an event corresponding to not A, which I denoted \(\neg A\). Let’s now define two new events that correspond to important everyday concepts: \(A\) and \(B\), and \(A\) or \(B\). To be precise:
| English statement: | Mathematical notation: |
|---|---|
| “\(A\) and \(B\)” both happen | \(A \cap B\) |
| at least one of “\(A\) or \(B\)” happens | \(A \cup B\) |
Since \(A\) and \(B\) are both defined in terms of our elementary events (the \(x\)s) we’re going to need to try to describe \(A \cap B\) and \(A \cup B\) in terms of our elementary events too. Can we do this? Yes we can The only way that both \(A\) and \(B\) can occur is if the elementary event that we observe turns out to belong to both \(A\) and \(B\). Thus “\(A \cap B\)” includes only those elementary events that belong to both \(A\) and \(B\)…
\[\begin{array}{rcl} A &=& (x_1, x_2, x_3) \\ B &=& (x_3, x_4) \\ A \cap B & = & (x_3) \end{array} \nonumber \]
So, um, the only way that I can wear “jeans” \((x_1, x_2, x_3)\) and “black pants” \((x_3, x_4)\) is if I wear “black jeans” \((x_3)\). Another victory for the bloody obvious.
At this point, you’re not going to be at all shocked by the definition of \(A \cup B\), though you’re probably going to be extremely bored by it. The only way that I can wear “jeans” or “black pants” is if the elementary pants that I actually do wear belongs to \(A\) or to \(B\), or to both. So…
\[\begin{array}{rcl} A &=& (x_1, x_2, x_3) \\ B &=& (x_3, x_4) \\ A \cup B & = & (x_1, x_2, x_3, x_4) \end{array} \nonumber \]
Oh yeah baby. Mathematics at its finest.
So, we’ve defined what we mean by \(A \cap B\) and \(A \cup B\). Now let’s assign probabilities to these events. More specifically, let’s start by verifying the rule that claims that:
\[P(A \cup B) = P(A) + P(B) - P(A \cap B) \nonumber \]
Using our definitions earlier, we know that \(A \cup B = (x_1, x_2, x_3, x_4)\), so
\[P(A \cup B) = P(x_1) + P(x_2) + P(x_3) + P(x_4) \nonumber \]
and making similar use of the fact that we know what elementary events belong to \(A\), \(B\) and \(A \cap B\)….
\[\begin{array}{rcl} P(A) &=& P(x_1) + P(x_2) + P(x_3) \\ P(B) &=& P(x_3) + P(x_4) \\ P(A \cap B) &=& P(x_3) \end{array} \nonumber \]
and therefore
\[\begin{array}{rcl} P(A) + P(B) - P(A \cap B) &=& P(x_1) + P(x_2) + P(x_3) + P(x_3) + P(x_4) - P(x_3) \\ &=& P(x_1) + P(x_2) + P(x_3) + P(x_4) \\ &=& P(A \cup B) \end{array} \nonumber \]
Done.
The next concept we need to define is the notion of “\(B\) given \(A\)”, which is typically written \(B | A\). Here’s what I mean: suppose that I get up one morning, and put on a pair of pants. An elementary event \(x\) has occurred. Suppose further I yell out to my wife (who is in the other room, and so cannot see my pants) “I’m wearing jeans today!”. Assuming that she believes that I’m telling the truth, she knows that \(A\) is true. Given that she knows that \(A\) has happened, what is the conditional probability that \(B\) is also true? Well, let’s think about what she knows. Here are the facts:
- The non-jeans events are impossible. If \(A\) is true, then we know that the only possible elementary events that could have occurred are \(x_1\), \(x_2\) and \(x_3\) (i.e.,the jeans). The non-jeans events \(x_4\) and \(x_5\) are now impossible, and must be assigned probability zero. In other words, our sample space has been restricted to the jeans events. But it’s still the case that the probabilities of these these events must sum to 1: we know for sure that I’m wearing jeans.
- She’s learned nothing about which jeans I’m wearing. Before I made my announcement that I was wearing jeans, she already knew that I was five times as likely to be wearing blue jeans (\(P(x_1) = 0.5\)) than to be wearing black jeans (\(P(x_3) = 0.1\)). My announcement doesn’t change this… I said nothing about what colour my jeans were, so it must remain the case that \(P(x_1) / P(x_3)\) stays the same, at a value of 5.
There’s only one way to satisfy these constraints: set the impossible events to have zero probability (i.e., \(P(x | A) = 0\) if \(x\) is not in \(A\)), and then divide the probabilities of all the others by \(P(A)\). In this case, since \(P(A) = 0.9\), we divide by 0.9. This gives:
| which pants? | elementary event | old prob, \(P(x)\) | new prob, \(P(x | A)\) |
|---|---|---|---|
| blue jeans | \(x_1\) | 0.5 | 0.556 |
| grey jeans | \(x_2\) | 0.3 | 0.333 |
| black jeans | \(x_3\) | 0.1 | 0.111 |
| black suit | \(x_4\) | 0 | 0 |
| blue tracksuit | \(x_5\) | 0.1 | 0 |
In mathematical terms, we say that
\[P(x | A) = \frac{P(x)}{P(A)} \nonumber \]
if \(x \in A\), and \(P(x|A) = 0\) otherwise. And therefore…
\[\begin{array}{rcl} P(B | A) &=& P(x_3 | A) + P(x_4 | A) \\ &=& \displaystyle\frac{P(x_3)}{P(A)} + 0 \\ &=& \displaystyle\frac{P(x_3)}{P(A)} \end{array} \nonumber \]
Now, recalling that \(A \cap B = (x_3)\), we can write this as
\[P(B | A) = \frac{P(A \cap B)}{P(A)} \nonumber \]
and if we multiply both sides by \(P(A)\) we obtain:
\[P(A \cap B) = P(B| A) P(A) \nonumber \]
which is the third rule that we had listed in the table.


