10.5: The Paired-samples t-test

Regardless of whether we’re talking about the Student test or the Welch test, an independent samples t-test is intended to be used in a situation where you have two samples that are, well, independent of one another. This situation arises naturally when participants are assigned randomly to one of two experimental conditions, but it provides a very poor approximation to other sorts of research designs. In particular, a repeated measures design – in which each participant is measured (with respect to the same outcome variable) in both experimental conditions – is not suited for analysis using independent samples t-tests. For example, we might be interested in whether listening to music reduces people’s working memory capacity. To that end, we could measure each person’s working memory capacity in two conditions: with music, and without music. In an experimental design such as this one,¹⁹⁴ each participant appears in both groups. This requires us to approach the problem in a different way; by using the paired samples t-test.

The Data

The data set that we’ll use this time comes from Dr. Chico’s class. In her class, students take two major tests, one early in the semester and one later in the semester. To hear her tell it, she runs a very hard class, one that most students find very challenging; but she argues that by setting hard assessments, students are encouraged to work harder. Her theory is that the first test is a bit of a “wake-up call” for students: when they realize how hard her class really is, they’ll work harder for the second test and get a better mark. Is she right? To test this, let’s have a look at the chico.sav file. The data file contains three variables: an id variable that identifies each student in the class, the grade_test1 variable that records the student grade for the first test, and the grade_test2 variable that has the grades for the second test. Here are  the first ten students:

At a glance, it does seem like the class is a hard one (most grades are between 50% and 60%), but it does look like there’s an improvement from the first test to the second one. If we take a quick look at the descriptive statistics

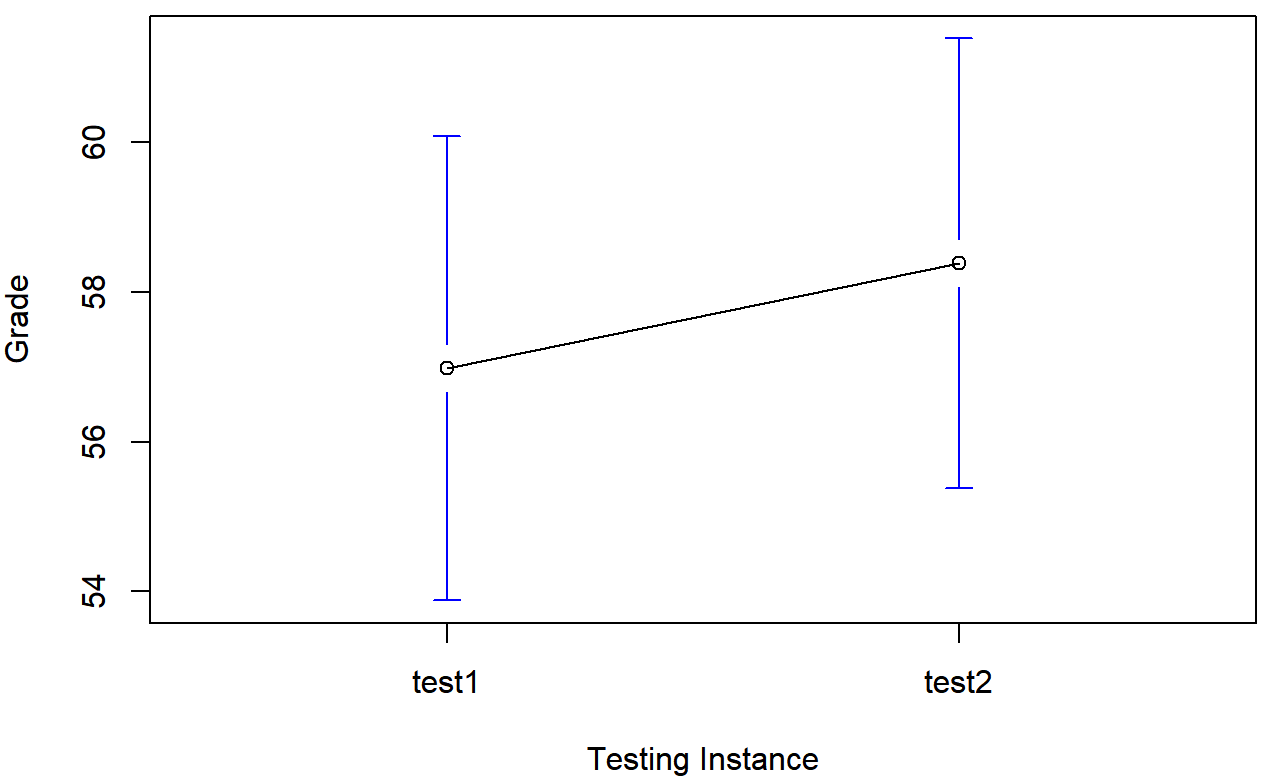
we see that this impression seems to be supported. Across all 20 students, the mean grade for the first test is 57%, but this rises to 58% for the second test. Although, given that the standard deviations are 6.6% and 6.4% respectively, it’s starting to feel like maybe the improvement is just illusory; maybe just random variation. This impression is reinforced when you see the means and confidence intervals plotted in Figure 10.11. If we were to rely on this plot alone, we’d come to the same conclusion that we got from looking at the descriptive statistics. Looking at how wide those confidence intervals are, we’d be tempted to think that the apparent improvement in student performance is pure chance.

Figure 10.11: Mean grade for test 1 and test 2, with associated 95% confidence intervals

Nevertheless, this impression is wrong. To see why, take a look at the scatterplot of the grades for test 1 against the grades for test 2. shown in Figure 10.12.

Figure 10.12: Scatterplot showing the individual grades for test 1 and test 2

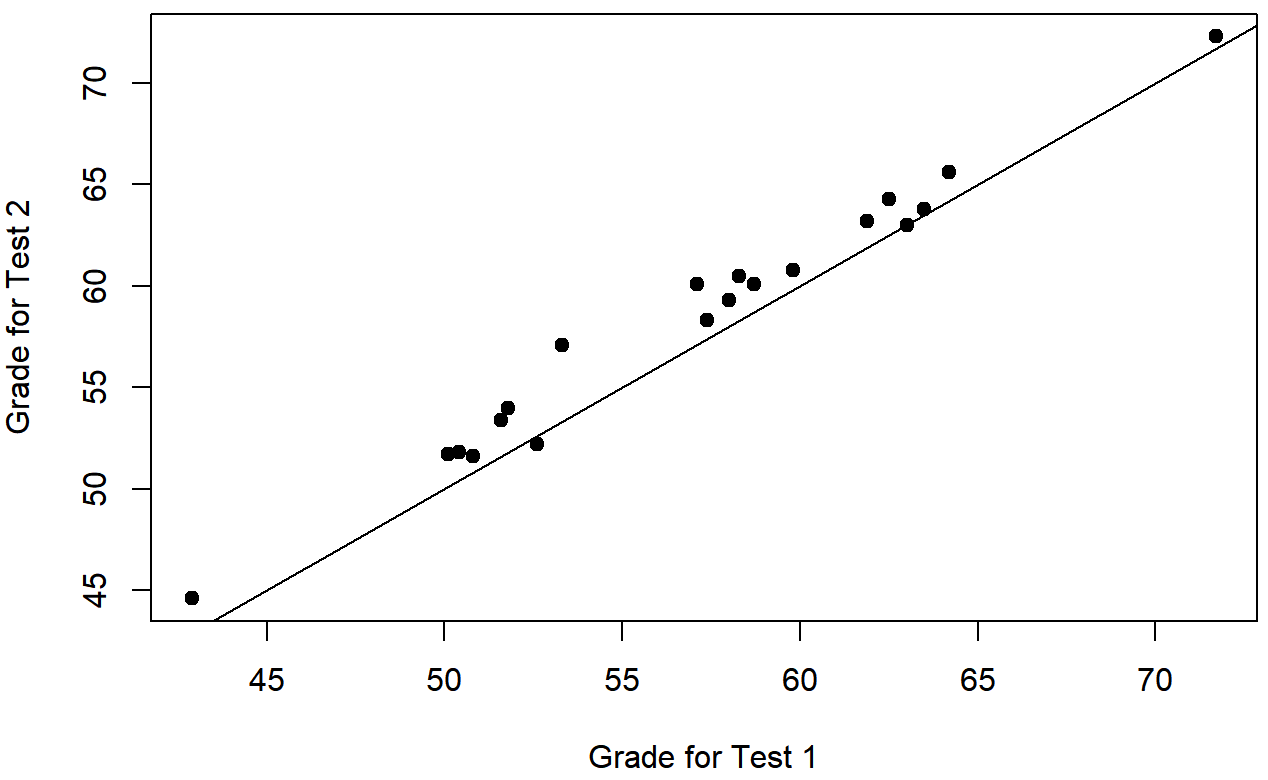
In this plot, each dot corresponds to the two grades for a given student: if their grade for test 1 (x co-ordinate) equals their grade for test 2 (y co-ordinate), then the dot falls on the line. Points falling above the line are the students that performed better on the second test. Critically, almost all of the data points fall above the diagonal line: almost all of the students do seem to have improved their grade, if only by a small amount. This suggests that we should be looking at the improvement made by each student from one test to the next, and treating that as our raw data. To do this, we’ll need to create a new variable for the improvement that each student makes, and add it to the chico.sav. The easiest way to do this is as follows:

This can be found in the Transform/Compute Variable... menu item. Here we are creating a variable called Improvement which will equal the score on test 2 - score on test 1. Why test 2 first? Well, we are testing the idea that scores improved from test 1 to test 2 so we might expect the difference score (improvement) to be positive, on average. If so, it just makes thing seem cleaner if we have positive numbers.

So now when we look at the data, we  get an output that looks like this:

 

Now that we’ve created and stored this improvement variable, we can draw a histogram showing the distribution of these improvement scores (using the Graph Builder), shown in Figure 10.13.

Figure 10.13: Histogram showing the improvement made by each student in Dr. Chico’s class. Notice that almost the entire distribution is above zero: the vast majority of students did improve their performance from the first test to the second one

When we look at histogram, it’s very clear that there is a real improvement here. The vast majority of the students scored higher on test 2 than on test 1, reflected in the fact that almost the entire histogram is above zero. In fact, if we compute a confidence interval for the population mean of this new variable,

we see that it is 95% certain that the true (population-wide) average improvement would lie between 0.95% and 1.86%. So you can see, qualitatively, what’s going on: there is a real “within student” improvement (everyone improves by about 1%), but it is very small when set against the quite large “between student” differences (student grades vary by about 20% or so).

What is the Paired Samples t-test?

In light of the previous exploration, let’s think about how to construct an appropriate t-test. One possibility would be to try to run an independent samples t-test using grade_test1 and grade_test2 as the variables of interest. However, this is clearly the wrong thing to do: the independent samples t-test assumes that there is no particular relationship between the two samples. Yet clearly that’s not true in this case, because of the repeated-measures structure to the data. To use the language that I introduced in the last section, if we were to try to do an independent samples t-test, we would be conflating the within subject differences (which is what we’re interested in testing) with the between subject variability (which we are not).

The solution to the problem is obvious, hopefully, since we already did all the hard work in the previous section. Instead of running an independent samples t-test on grade_test1 and grade_test2, we run a one-sample t-test on the within-subject difference variable, improvement. To formalize this slightly, if X_i1 is the score that the i-th participant obtained on the first variable, and X_i2 is the score that the same person obtained on the second one, then the difference score is:

D_i=X_i1−X_i2

Notice that the difference scores is variable 1 minus variable 2 and not the other way around, so if we want improvement to correspond to a positive valued difference, we actually want “test 2” to be our “variable 1”. Equally, we would say that μ_D=μ₁−μ₂ is the population mean for this difference variable. So, to convert this to a hypothesis test, our null hypothesis is that this mean difference is zero; the alternative hypothesis is that it is not:

H₀:μ_D=0

H₁:μ_D≠0

(this is assuming we’re talking about a two-sided test here). This is more or less identical to the way we described the hypotheses for the one-sample t-test: the only difference is that the specific value that the null hypothesis predicts is 0. And so our t-statistic is defined in more or less the same way too. If we let \(\ \bar{D}\) denote the mean of the difference scores, then

\(t=\frac{\bar{D}}{\operatorname{SE}(\bar{D})}\)

which is

\(t=\frac{\bar{D}}{\hat{\sigma}_{D} / \sqrt{N}}\)

where \(\ \hat{\sigma_D}\) is the standard deviation of the difference scores. Since this is just an ordinary, one-sample t-test, with nothing special about it, the degrees of freedom are still N−1. And that’s it: the paired samples t-test really isn’t a new test at all: it’s a one-sample t-test, but applied to the difference between two variables. It’s actually very simple; the only reason it merits a discussion as long as the one we’ve just gone through is that you need to be able to recognize when a paired samples test is appropriate and to understand why it’s better than an independent samples t-test.

Doing the Test in SPSS

How do you do a paired samples t-test in SPSS?. One possibility is to follow the process outlined above: create a “difference” variable and then run a one-sample t-test on that. Since we’ve already created a variable called improvement, let’s do that:

Note that unlike our example in the previous section, here our Test Value will be equal to zero because the null hypothesis is that there will be no difference between test 1 and test 2. Once we run this we get:

The output here is (obviously) formatted exactly the same as it was the last time we used the One-Sample T Test function (Section 10.2), and it confirms our intuition. There’s an average improvement of 1.405% from test 1 to test 2, and this is significantly different from 0 (t(19)=6.48, p<.001).

However, suppose you’re lazy (and let me tell you, statisticians are lazy) and you don’t want to go to all the effort of creating a new variable. Or perhaps you just want to keep the difference between one-sample and paired-samples tests clear in your head. If so, you can use the Paired Samples T Test function:

Note that this dialog has space for two variables, which in this case are the first and second test scores for each student. Note, too, that the variables have been entered into the dialog with test 2 going first and then test 1. This is because variable 2 will be subtracted from variable 1, and if we believe that test 2 scores are higher than test 1 scores, we would enter the variables as shown so that the difference is a positive number. If you enter test 1 first and then test 2, the result will be identical except that the t-statistic will be negative. Let's click on OK and see what we get:

The numbers are identical to those that come from the one-sample test, which of course they have to be given that the paired samples t-test is just a one-sample test under the hood. However, the output is a bit more detailed. This time around the descriptive statistics block shows you the means and standard deviations for the original variables, as well as for the difference variable. The null hypothesis and the alternative hypothesis are now framed in terms of the original variables rather than the difference score, but you should keep in mind that in a paired samples test it’s still the difference score being tested. The statistical information at the bottom about the test result is of course the same as before.