6.2: Meta-Analysis
- Page ID
- 1754
Learning Objectives
- To use meta-analysis when you want to combine the results from different studies, making the equivalent of one big study, so see if an overall effect is significant.
When to use it
Meta-analysis is a statistical technique for combining the results of different studies to see if the overall effect is significant. People usually do this when there are multiple studies with conflicting results—a drug does or does not work, reducing salt in food does or does not affect blood pressure, that sort of thing. Meta-analysis is a way of combining the results of all the studies; ideally, the result is the same as doing one study with a really big sample size, one large enough to conclusively demonstrate an effect if there is one, or conclusively reject an effect if there isn't one of an appreciable size.
I'm going to outline the general steps involved in doing a meta-analysis, but I'm not going to describe it in sufficient detail that you could do one yourself; if that's what you want to do, see Berman and Parker (2002), Gurevitch and Hedges (2001), Hedges and Olkin (1985), or some other book. Instead, I hope to explain some of the basic steps of a meta-analysis, so that you'll know what to look for when you read the results of a meta-analysis that someone else has done.
Decide which studies to include
Before you start collecting studies, it's important to decide which ones you're going to include and which you'll exclude. Your criteria should be as objective as possible; someone else should be able to look at your criteria and then include and exclude the exact same studies that you did. For example, if you're looking at the effects of a drug on a disease, you might decide that only double-blind, placebo-controlled studies are worth looking at, or you might decide that single-blind studies (where the investigator knows who gets the placebo, but the patient doesn't) are acceptable; or you might decide that any study at all on the drug and the disease should be included.
You shouldn't use sample size as a criterion for including or excluding studies. The statistical techniques used for the meta-analysis will give studies with smaller sample sizes the lower weight they deserve.
Finding studies
The next step in a meta-analysis is finding all of the studies on the subject. A critical issue in meta-analysis is what's known as the "file-drawer effect"; people who do a study and fail to find a significant result are less likely to publish it than if they find a significant result. Studies with non-significant results are generally boring; it's difficult to get up the enthusiasm to write them up, and it's difficult to get them published in decent journals. It's very tempting for someone with a bunch of boring, non-significant data to quietly put it in a file drawer, say "I'll write that up when I get some free time," and then never actually get enough free time.
The reason the file-drawer effect is important to a meta-analysis is that even if there is no real effect, \(5\%\) of studies will show a significant result at the \(P<0.05\) level; that's what \(P<0.05\) means, after all, that there's a \(5\%\) probability of getting that result if the null hypothesis is true. So if \(100\) people did experiments to see whether thinking about long fingernails made your fingernails grow faster, you'd expect \(95\) of them to find non-significant results. They'd say to themselves, "Well, that didn't work out, maybe I'll write it up for the Journal of Fingernail Science someday," then go on to do experiments on whether thinking about long hair made your hair grow longer and never get around to writing up the fingernail results. The \(5\) people who did find a statistically significant effect of thought on fingernail growth would jump up and down in excitement at their amazing discovery, then get their papers published in Science or Nature. If you did a meta-analysis on the published results on fingernail thought and fingernail growth, you'd conclude that there was a strong effect, even though the null hypothesis is true.
To limit the file-drawer effect, it's important to do a thorough literature search, including really obscure journals, then try to see if there are unpublished experiments. To find out about unpublished experiments, you could look through summaries of funded grant proposals, which for government agencies such as NIH and NSF are searchable online; look through meeting abstracts in the appropriate field; write to the authors of published studies; and send out appeals on e-mail mailing lists.
You can never be 100% sure that you've found every study on your topic ever done, but that doesn't mean you can cynically dismiss the results of every meta-analysis with the magic words "file-drawer effect." If your meta-analysis of the effects of thought on fingernail growth found \(5\) published papers with individually significant results, and a thorough search using every resource you could think of found \(5\) other unpublished studies with non-significant results, your meta-analysis would probably show a significant overall effect, and you should probably believe it. For the \(5\) significant results to all be false positives, there would have to be something like \(90\) additional unpublished studies that you didn't know about, and surely the field of fingernail science is small enough that there couldn't be that many studies that you haven't heard of. There are ways to estimate how many unpublished, non-significant studies there would have to be to make the overall effect in a meta-analysis non-significant. If that number is absurdly large, you can be more confident that your significant meta-analysis is not due to the file-drawer effect.
Extract the information
If the goal of a meta-analysis is to estimate the mean difference between two treatments, you need the means, sample sizes, and a measure of the variation: standard deviation, standard error, or confidence interval. If the goal is to estimate the association between two measurement variables, you need the slope of the regression, the sample size, and the \(r^2\). Hopefully this information is presented in the publication in numerical form. Boring, non-significant results are more likely to be presented in an incomplete form, so you shouldn't be quick to exclude papers from your meta-analysis just because all the necessary information isn't presented in easy-to-use form in the paper. If it isn't, you might need to write the authors, or measure the size and position of features on published graphs.
Do the meta-analysis
The basic idea of a meta-analysis is that you take a weighted average of the difference in means, slope of a regression, or other statistic across the different studies. Experiments with larger sample sizes get more weight, as do experiments with smaller standard deviations or higher \(r^2\) values. You can then test whether this common estimate is significantly different from zero.
Interpret the results
Meta-analysis was invented to be a more objective way of surveying the literature on a subject. A traditional literature survey consists of an expert reading a bunch of papers, dismissing or ignoring those that they don't think are very good, then coming to some conclusion based on what they think are the good papers. The problem with this is that it's easier to see the flaws in papers that disagree with your preconceived ideas about the subject and dismiss them, while deciding that papers that agree with your position are acceptable.
The problem with meta-analysis is that a lot of scientific studies really are crap, and pushing a bunch of little piles of crap together just gives you one big pile of crap. For example, let's say you want to know whether moonlight-energized water cures headaches. You expose some water to moonlight, give little bottles of it to \(20\) of your friends, and say "Take this the next time you have a headache." You ask them to record the severity of their headache on a \(10\)-point scale, drink the moonlight-energized water, then record the severity of their headache \(30\) minutes later. This study is crap—any reported improvement could be due to the placebo effect, or headaches naturally getting better with time, or moonlight-energized water curing dehydration just as well as regular water, or your friends lying because they knew you wanted to see improvement. If you include this crappy study in a big meta-analysis of the effects of moonlight-energized water on pain, no amount of sophisticated statistical analysis is going to make its crappiness go away.
You're probably thinking "moonlight-energized water" is another ridiculously absurd thing that I just made up, aren't you? That no one could be stupid enough to believe in such a thing? Unfortunately, there are people that stupid.
The hard work of a meta-analysis is finding all the studies and extracting the necessary information from them, so it's tempting to be impressed by a meta-analysis of a large number of studies. A meta-analysis of \(50\) studies sounds more impressive than a meta-analysis of \(5\) studies; it's \(10\) times as big and represents \(10\) times as much work, after all. However, you have to ask yourself, "Why do people keep studying the same thing over and over? What motivated someone to do that \(50^{th}\) experiment when it had already been done \(49\) times before?" Often, the reason for doing that \(50^{th}\) study is that the preceding \(49\) studies were crappy in some way. If you've got \(50\) studies, and \(5\) of them are better by some objective criteria than the other \(45\), you'd be better off using just the \(5\) best studies in your meta-analysis.
Example
Chondroitin is a polysaccharide derived from cartilage. It is commonly used by people with arthritis in the belief that it will reduce pain, but clinical studies of its effectiveness have yielded conflicting results. Reichenbach et al. (2007) performed a meta-analysis of studies on chondroitin and arthritis pain of the knee and hip. They identified relevant studies by electronically searching literature databases and clinical trial registries, manual searching of conference proceedings and the reference lists of papers, and contacting various experts in the field. Only trials that involved comparing patients given chondroitin with control patients were used; the control could be either a placebo or no treatment. They obtained the necessary information about the amount of pain and the variation by measuring graphs in the papers, if necessary, or by contacting the authors.
The initial literature search yielded \(291\) potentially relevant reports, but after eliminating those that didn't use controls, those that didn't randomly assign patients to the treatment and control groups, those that used other substances in combination with chondroitin, those for which the necessary information wasn't available, etc., they were left with \(20\) trials.
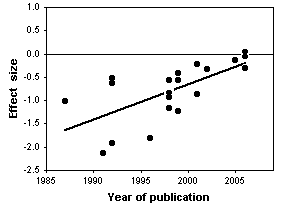
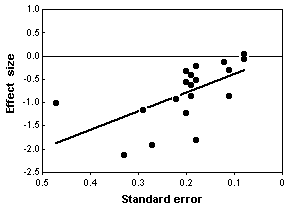
The statistical analysis of all \(20\) trials showed a large, significant effect of chondroitin in reducing arthritis pain. However, the authors noted that earlier studies, published in 1987-2001, had large effects, while more recent studies (which you would hope are better) showed little or no effect of chondroitin. In addition, trials with smaller standard errors (due to larger sample sizes or less variation among patients) showed little or no effect. In the end, Reichenbach et al. (2007) analyzed just the three largest studies with what they considered the best designs, and they showed essentially zero effect of chondroitin. They concluded that there's no good evidence that chondroitin is effective for knee and hip arthritis pain. Other researchers disagree with their conclusion (Goldberg et al. 2007, Pelletier 2007); while a careful meta-analysis is a valuable way to summarize the available information, it is unlikely to provide the last word on a question that has been addressed with large numbers of poorly designed studies.
References
- Berman, N.G., and R.A. Parker. 2002. Meta-analysis: neither quick nor easy. BMC Medical Research Methods 2:10. [A good readable introduction to medical meta-analysis, with lots of useful references.]
- Goldberg, H., A. Avins, and S. Bent. 2007. Chondroitin for osteoarthritis of the knee or hip. Annals of Internal Medicine 147: 883.
- Gurevitch, J., and L.V. Hedges. 2001. Meta-analysis: combining the results of independent experiments. pp. 347-369 in Design and Analysis of Ecological Experiments, S.M. Scheiner and J. Gurevitch, eds. Oxford University Press, New York. [Discusses the use of meta-analysis in ecology, a different perspective than the more common uses of meta-analysis in medical research and the social sciences.]
- Hedges, L.V., and I. Olkin. 1985. Statistical methods for meta-analysis. Academic Press, London. [I haven't read this, but apparently this is the classic text on meta-analysis.]
- Pelletier, J.-P. 2007. Chondroitin for osteoarthritis of the knee or hip. Annals of Internal Medicine 147: 883-884.
- Reichenbach, S., R. Sterchi, M. Scherer, S. Trelle, E. Bürgi, U. Bürgi, P.A. Dieppe, and P. Jüni. 2007. Meta-analysis: Chondroitin for osteoarthritis of the knee or hip. Annals of Internal Medicine 146: 580-590.


