2.1: Three Popular Data Displays
- Page ID
- 555
- To learn to interpret the meaning of three graphical representations of sets of data: stem and leaf diagrams, frequency histograms, and relative frequency histograms.
A well-known adage is that “a picture is worth a thousand words.” This saying proves true when it comes to presenting statistical information in a data set. There are many effective ways to present data graphically. The three graphical tools that are introduced in this section are among the most commonly used and are relevant to the subsequent presentation of the material in this book.
Stem and Leaf Diagrams
Suppose \(30\) students in a statistics class took a test and made the following scores:
\[\begin{array}{r}86 & 80 & 25 & 77 & 73 & 76 & 100 & 90 & 69 & 93 \\ 90 & 83 & 70 & 73 & 73 & 70 & 90 & 83 & 71 & 95 \\ 40 & 58 & 68 & 69 & 100 & 78 & 87 & 97 & 92 & 74\end{array} \nonumber \]
How did the class do on the test? A quick glance at the set of \(30\) numbers does not immediately give a clear answer. However the data set may be reorganized and rewritten to make relevant information more visible. One way to do so is to construct a stem and leaf diagram as shown in Figure \(\PageIndex{1}\) The numbers in the tens place, from \(2\) through \(9\), and additionally the number \(10\), are the “stems,” and are arranged in numerical order from top to bottom to the left of a vertical line. The number in the units place in each measurement is a “leaf,” and is placed in a row to the right of the corresponding stem, the number in the tens place of that measurement. Thus the three leaves \(9, 8, \text{and} \; 9\) in the row headed with the stem \(6\) correspond to the three exam scores in the \(60s, 69\) (in the first row of data), \(68\) (in the third row), and \(69\) (also in the third row).

The display is made even more useful for some purposes by rearranging the leaves in numerical order, as shown in Figure \(\PageIndex{2}\). Either way, with the data reorganized certain information of interest becomes apparent immediately. There are two perfect scores; three students made scores under \(60\); most students scored in the \(70s, 80s\; \text{and} \; 90s\); and the overall average is probably in the high \(70s\; \text{or low}\; 80s\).

In this example the scores have a natural stem (the tens place) and leaf (the ones place). One could spread the diagram out by splitting each tens place number into lower and upper categories. For example, all the scores in the \(80s\) may be represented on two separate stems, lower \(80s\) and upper \(80s\):
\[\begin{array}{r|lcc}8 & 0 & 3 & 3 \\ 8 & 6 & 7 &\end{array} \nonumber \]
The definitions of stems and leaves are flexible in practice. The general purpose of a stem and leaf diagram is to provide a quick display of how the data are distributed across the range of their values; some improvisation could be necessary to obtain a diagram that best meets that goal.
Note that all of the original data can be recovered from the stem and leaf diagram. This will not be true in the next two types of graphical displays.
Frequency Histograms
The stem and leaf diagram is not practical for large data sets, so we need a different, purely graphical way to represent data. A frequency histogram is such a device. We will illustrate it using the same data set from the previous subsection. For the \(30\) scores on the exam, it is natural to group the scores on the standard ten-point scale, and count the number of scores in each group. Thus there are two \(100s\), seven scores in the \(90s\), six in the \(80s\), and so on. We then construct the diagram shown in Figure \(\PageIndex{3}\) by drawing for each group, or class, a vertical bar whose length is the number of observations in that group. In our example, the bar labeled \(100\) is \(2\) units long, the bar labeled \(90\) is \(7\) units long, and so on. While the individual data values are lost, we know the number in each class. This number is called the frequency of the class, hence the name frequency histogram.
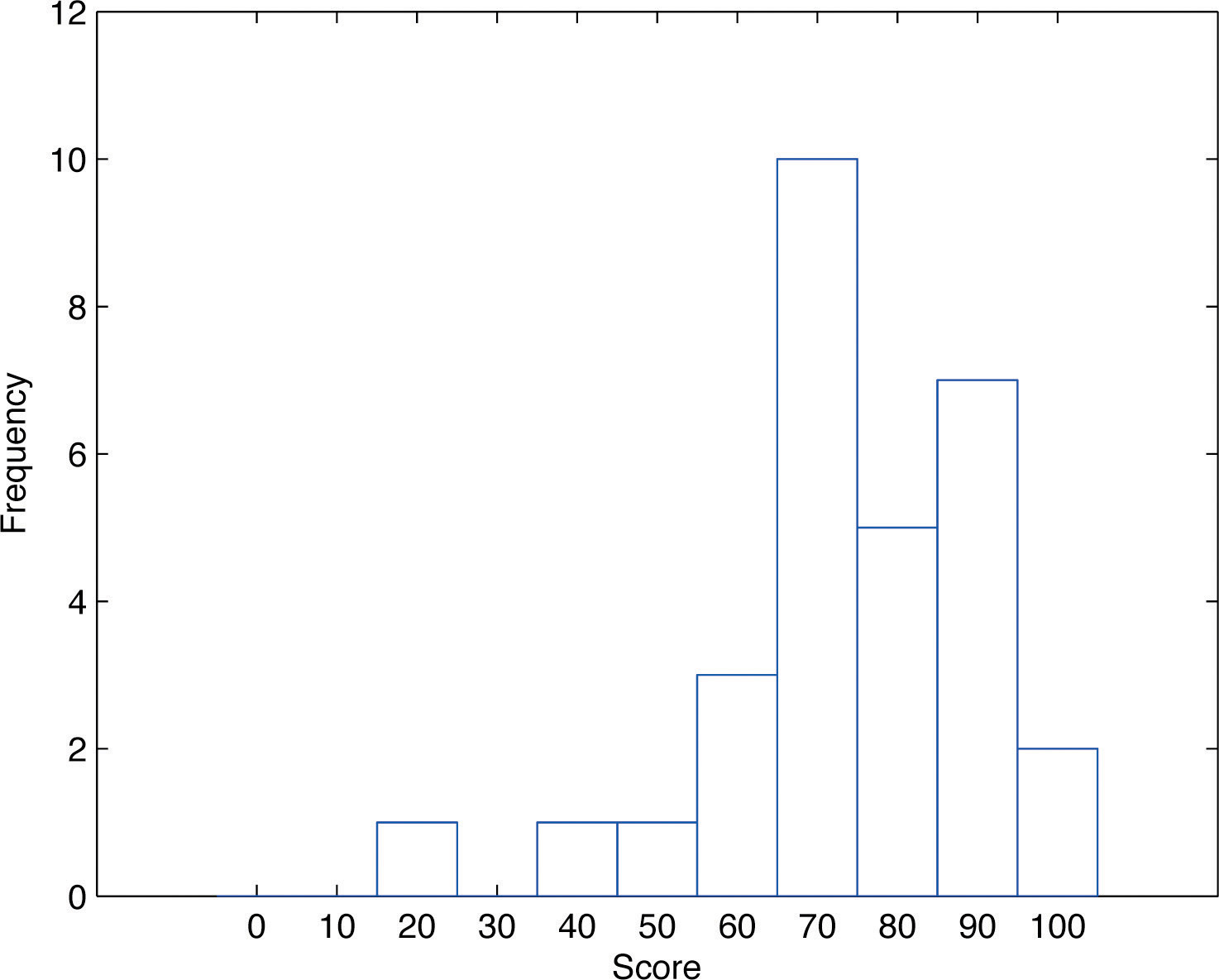
The same procedure can be applied to any collection of numerical data. Observations are grouped into several classes and the frequency (the number of observations) of each class is noted. These classes are arranged and indicated in order on the horizontal axis (called the x-axis), and for each group a vertical bar, whose length is the number of observations in that group, is drawn. The resulting display is a frequency histogram for the data. The similarity in Figure \(\PageIndex{1}\) and Figure \(\PageIndex{3}\) is apparent, particularly if you imagine turning the stem and leaf diagram on its side by rotating it a quarter turn counterclockwise.
In general, the definition of the classes in the frequency histogram is flexible. The general purpose of a frequency histogram is very much the same as that of a stem and leaf diagram, to provide a graphical display that gives a sense of data distribution across the range of values that appear.
We will not discuss the process of constructing a histogram from data since in actual practice it is done automatically with statistical software or even handheld calculators.
Relative Frequency Histograms
In our example of the exam scores in a statistics class, five students scored in the \(80s\). The number \(5\) is the frequency of the group labeled “\(80s\).” Since there are \(30\) students in the entire statistics class, the proportion who scored in the \(80s\) is \(5/30\). The number \(5/30\), which could also be expressed as \(0.1 \bar{6} \approx . 1667\), or as \(16.67\% \), is the relative frequency of the group labeled “\(80s\).” Every group (the \(70s\), the \(80s\), and so on) has a relative frequency. We can thus construct a diagram by drawing for each group, or class, a vertical bar whose length is the relative frequency of that group. For example, the bar for the \(80s\) will have length \(5/30\) unit, not \(5\) units. The diagram is a relative frequency histogram for the data, and is shown in Figure \(\PageIndex{4}\). It is exactly the same as the frequency histogram except that the vertical axis in the relative frequency histogram is not frequency but relative frequency.
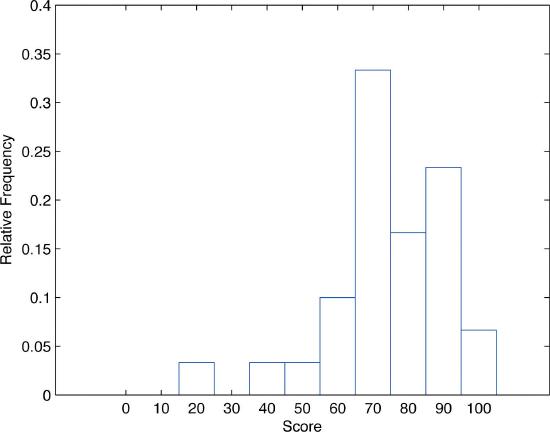
The same procedure can be applied to any collection of numerical data. Classes are selected, the relative frequency of each class is noted, the classes are arranged and indicated in order on the horizontal axis, and for each class a vertical bar, whose length is the relative frequency of the class, is drawn. The resulting display is a relative frequency histogram for the data. A key point is that now if each vertical bar has width \(1\) unit, then the total area of all the bars is \(1\) or \(100\% \).
Although the histograms in Figure \(\PageIndex{3}\) and Figure \(\PageIndex{4}\) have the same appearance, the relative frequency histogram is more important for us, and it will be relative frequency histograms that will be used repeatedly to represent data in this text. To see why this is so, reflect on what it is that you are actually seeing in the diagrams that quickly and effectively communicates information to you about the data. It is the relative sizes of the bars. The bar labeled “\(70s\)” in either figure takes up \(1/3\) of the total area of all the bars, and although we may not think of this consciously, we perceive the proportion \(1/3\) in the figures, indicating that a third of the grades were in the \(70s\). The relative frequency histogram is important because the labeling on the vertical axis reflects what is important visually: the relative sizes of the bars.
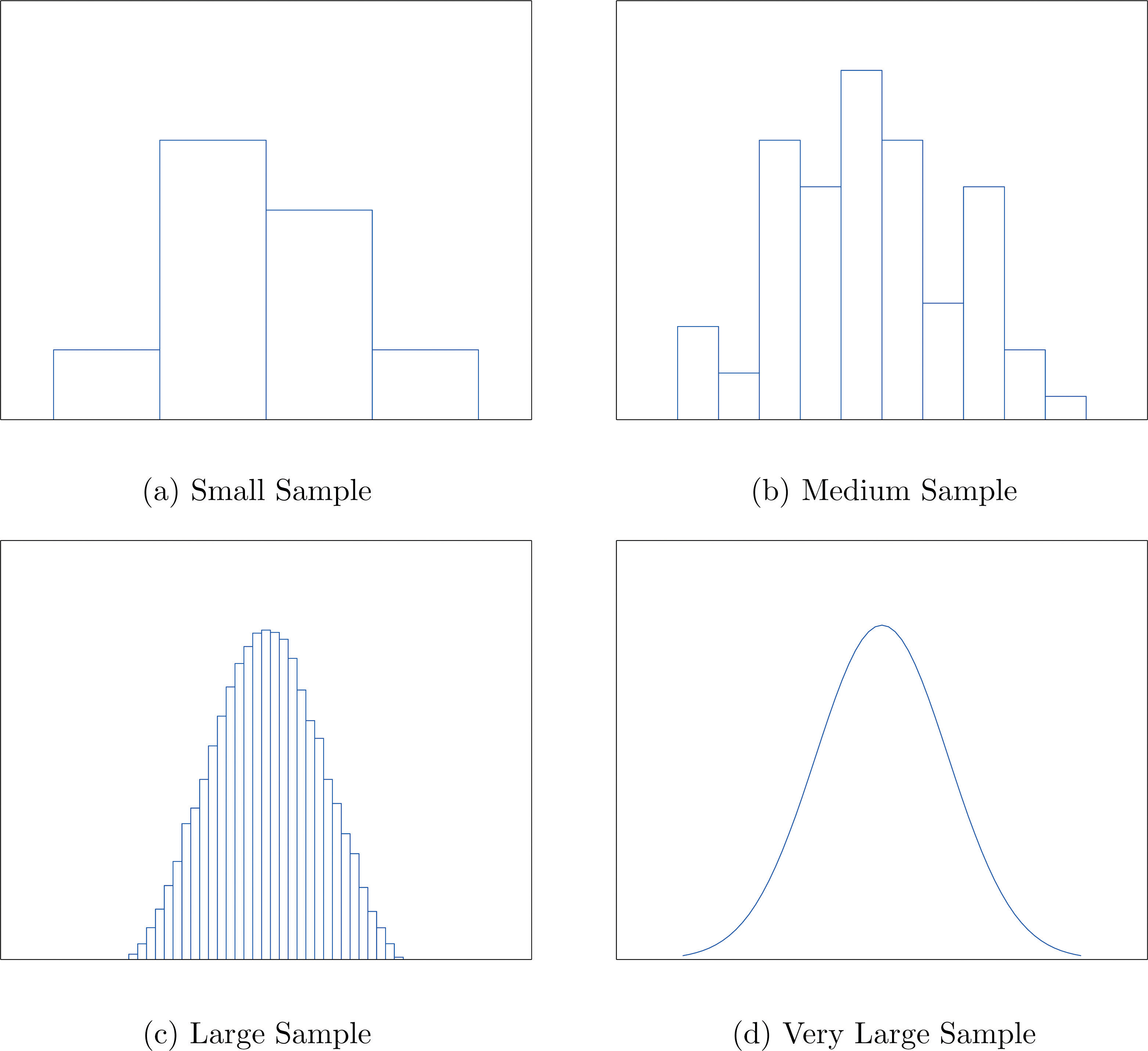
When the size n of a sample is small only a few classes can be used in constructing a relative frequency histogram. Such a histogram might look something like the one in panel (a) of Figure \(\PageIndex{5}\). If the sample size \(n\) were increased, then more classes could be used in constructing a relative frequency histogram and the vertical bars of the resulting histogram would be finer, as indicated in panel (b) of Figure \(\PageIndex{5}\). For a very large sample the relative frequency histogram would look very fine, like the one in (c) of Figure \(\PageIndex{5}\). If the sample size were to increase indefinitely then the corresponding relative frequency histogram would be so fine that it would look like a smooth curve, such as the one in panel (d) of Figure \(\PageIndex{5}\).
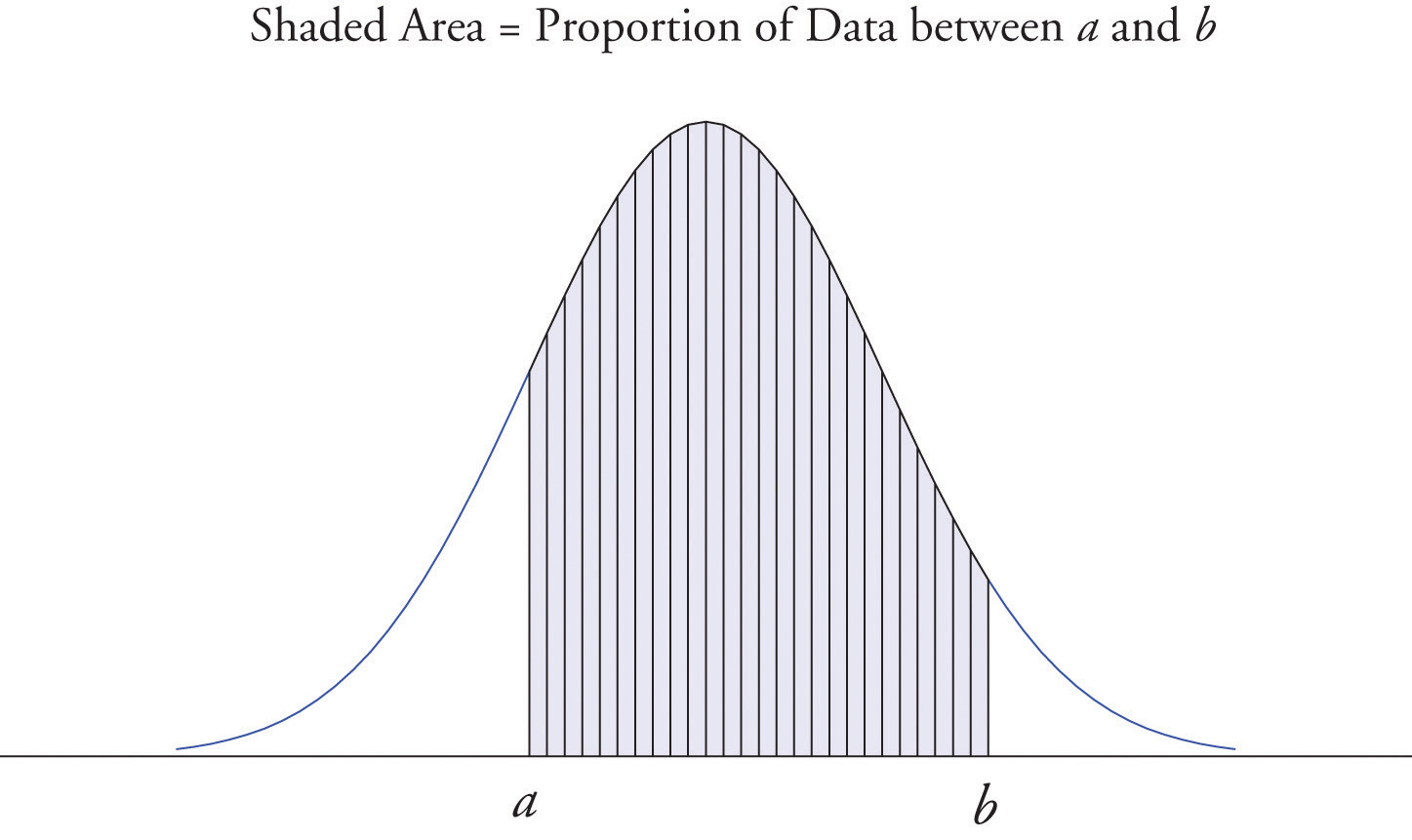
It is common in statistics to represent a population or a very large data set by a smooth curve. It is good to keep in mind that such a curve is actually just a very fine relative frequency histogram in which the exceedingly narrow vertical bars have disappeared. Because the area of each such vertical bar is the proportion of the data that lies in the interval of numbers over which that bar stands, this means that for any two numbers \(a\) and \(b\), the proportion of the data that lies between the two numbers \(a\) and \(b\) is the area under the curve that is above the interval (\(a,b\)) in the horizontal axis. This is the area shown in Figure \(\PageIndex{6}\). In particular the total area under the curve is \(1\), or \(100\% \).
- Graphical representations of large data sets provide a quick overview of the nature of the data.
- A population or a very large data set may be represented by a smooth curve. This curve is a very fine relative frequency histogram in which the exceedingly narrow vertical bars have been omitted.
- When a curve derived from a relative frequency histogram is used to describe a data set, the proportion of data with values between two numbers \(a\) and \(b\) is the area under the curve between \(a\) and \(b\), as illustrated in Figure \(\PageIndex{6}\).


