5.4: Gambler's Fallacy
- Page ID
- 2107
Learning Objectives
- Understand the link between the number of trials and expected outcome of probability distributions
Instructions
The gambler's fallacy involves beliefs about sequences of independent events. By definition, if two events are independent, the occurrence of one event does not affect the occurrence of the second. For example, if a fair coin is flipped twice, the occurrence of a head on the first flip does not affect the outcome of the second flip.
What if a coin is flipped five times and comes up heads each time. Is a tail "due" and therefore more likely than not to occur on the next flip. Since the events are independent, the answer is "no."
The gambler's fallacy is mistakenly believing that the answer is "yes." Believers in the fallacy argue correctly that in the long run, the proportion of heads will be \(0.50\). Or, stated more precisely, as the number of flips approaches infinity, the proportion of heads approaches \(0.50\). Doesn't this imply that there must be some natural adjustment occurring, compensating for a string of heads with the later occurrence of more tails?
This simulation allows you to explore this question yourself. You can simulate the flipping of a single coin by clicking the "flip once" button. The number of flips (\(n\)), the number of heads, the number of tails, the difference between the number of heads and the number of tails, and the proportion of heads are all recorded and displayed.
To speed things up, you can click the "Flip \(100\) times" or the "Flip \(1000\) times" buttons. The "reset" button clears all the data. The lower portion of the simulation allows you to simulate \(25,000\) flips at a time. After you click the "Flip \(25,000\) times and draw graphs" button, the graph on the left will plot the difference between the number of heads and tails as a function of the number of coin flips. The graph on the right will plot the proportion of heads as a function of the number of coin flips.
Illustrated Instructions
The gambler's fallacy demonstration allows you to flip a fair coin in a variety of increments. Each time you click one of these buttons the total number of coin flips is increased by the increment on the respective button.
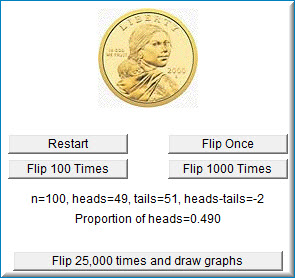
The screenshot below shows what happens when you click the "Flip \(25,000\) times...". The demonstration draws to graphs the first of which shows the Heads minus Tails for all trials and the second shows the proportion of heads for all trials. Clicking this button repeatedly increments the number of trials and adjusts the graphs accordingly.