9.1: Introduction to Sampling Distributions
- Page ID
- 2131
Learning Objectives
- Define inferential statistics
- Graph a probability distribution for the mean of a discrete variable
- Describe a sampling distribution in terms of "all possible outcomes"
- Describe a sampling distribution in terms of repeated sampling
- Describe the role of sampling distributions in inferential statistics
- Define the standard error of the mean
Suppose you randomly sampled \(10\) people from the population of women in Houston, Texas, between the ages of \(21\) and \(35\) years and computed the mean height of your sample. You would not expect your sample mean to be equal to the mean of all women in Houston. It might be somewhat lower or it might be somewhat higher, but it would not equal the population mean exactly. Similarly, if you took a second sample of \(10\) people from the same population, you would not expect the mean of this second sample to equal the mean of the first sample.
Recall that inferential statistics concern generalizing from a sample to a population. A critical part of inferential statistics involves determining how far sample statistics are likely to vary from each other and from the population parameter. (In this example, the sample statistics are the sample means and the population parameter is the population mean.) As the later portions of this chapter show, these determinations are based on sampling distributions.
Discrete Distributions
We will illustrate the concept of sampling distributions with a simple example. Figure \(\PageIndex{1}\) shows three pool balls, each with a number on it. Two of the balls are selected randomly (with replacement) and the average of their numbers is computed.

All possible outcomes are shown below in Table \(\PageIndex{1}\).
| Outcome | Ball 1 | Ball 2 | Mean |
|---|---|---|---|
| 1 | 1 | 1 | 1.0 |
| 2 | 1 | 2 | 1.5 |
| 3 | 1 | 3 | 2.0 |
| 4 | 2 | 1 | 1.5 |
| 5 | 2 | 2 | 2.0 |
| 6 | 2 | 3 | 2.5 |
| 7 | 3 | 1 | 2.0 |
| 8 | 3 | 2 | 2.5 |
| 9 | 3 | 3 | 3.0 |
Notice that all the means are either \(1.0\), \(1.5\), \(2.0\), \(2.5\), or \(3.0\). The frequencies of these means are shown in Table \(\PageIndex{2}\). The relative frequencies are equal to the frequencies divided by nine because there are nine possible outcomes.
| Mean | Frequency | Relative Frequency |
|---|---|---|
| 1.0 | 1 | 0.111 |
| 1.5 | 2 | 0.222 |
| 2.0 | 3 | 0.333 |
| 2.5 | 2 | 0.222 |
| 3.0 | 1 | 0.111 |
Figure \(\PageIndex{2}\) shows a relative frequency distribution of the means based on Table \(\PageIndex{2}\). This distribution is also a probability distribution since the \(Y\)-axis is the probability of obtaining a given mean from a sample of two balls in addition to being the relative frequency.
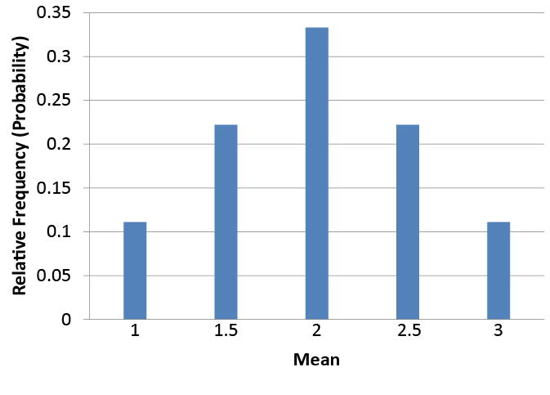
The distribution shown in Figure \(\PageIndex{2}\) is called the sampling distribution of the mean. Specifically, it is the sampling distribution of the mean for a sample size of \(2\) (\(N = 2\)). For this simple example, the distribution of pool balls and the sampling distribution are both discrete distributions. The pool balls have only the values \(1\), \(2\), and \(3\), and a sample mean can have one of only five values shown in Table \(\PageIndex{2}\).
There is an alternative way of conceptualizing a sampling distribution that will be useful for more complex distributions. Imagine that two balls are sampled (with replacement) and the mean of the two balls is computed and recorded. Then this process is repeated for a second sample, a third sample, and eventually thousands of samples. After thousands of samples are taken and the mean computed for each, a relative frequency distribution is drawn. The more samples, the closer the relative frequency distribution will come to the sampling distribution shown in Figure \(\PageIndex{2}\). As the number of samples approaches infinity, the relative frequency distribution will approach the sampling distribution. This means that you can conceive of a sampling distribution as being a relative frequency distribution based on a very large number of samples. To be strictly correct, the relative frequency distribution approaches the sampling distribution as the number of samples approaches infinity.
| Outcome | Ball 1 | Ball 2 | Range |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 2 | 1 | 2 | 1 |
| 3 | 1 | 3 | 2 |
| 4 | 2 | 1 | 1 |
| 5 | 2 | 2 | 0 |
| 6 | 2 | 3 | 1 |
| 7 | 3 | 1 | 2 |
| 8 | 3 | 2 | 1 |
| 9 | 3 | 3 | 0 |
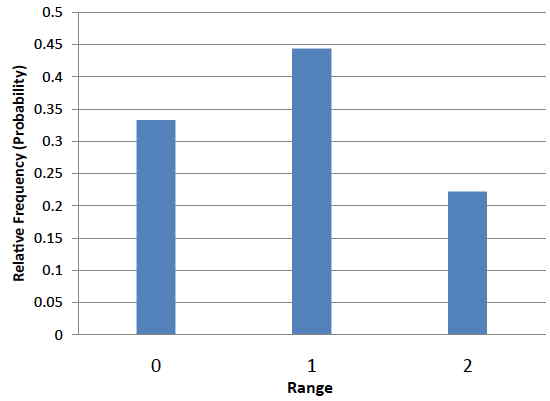
It is important to keep in mind that every statistic, not just the mean, has a sampling distribution. For example, Table \(\PageIndex{3}\) shows all possible outcomes for the range of two numbers (larger number minus the smaller number). Table \(\PageIndex{4}\) shows the frequencies for each of the possible ranges and Figure \(\PageIndex{3}\) shows the sampling distribution of the range.
| Range | Frequency | Relative Frequency |
|---|---|---|
| 0 | 3 | 0.333 |
| 1 | 4 | 0.444 |
| 2 | 2 | 0.222 |
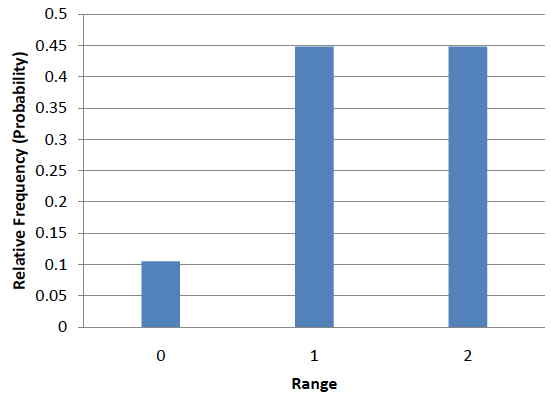
It is also important to keep in mind that there is a sampling distribution for various sample sizes. For simplicity, we have been using \(N = 2\). The sampling distribution of the range for \(N = 3\) is shown in Figure \(\PageIndex{4}\).
Continuous Distributions
In the previous section, the population consisted of three pool balls. Now we will consider sampling distributions when the population distribution is continuous. What if we had a thousand pool balls with numbers ranging from \(0.001\) to \(1.000\) in equal steps? (Although this distribution is not really continuous, it is close enough to be considered continuous for practical purposes.) As before, we are interested in the distribution of means we would get if we sampled two balls and computed the mean of these two balls. In the previous example, we started by computing the mean for each of the nine possible outcomes. This would get a bit tedious for this example since there are \(1,000,000\) possible outcomes (\(1,000\) for the first ball x \(1,000\) for the second). Therefore, it is more convenient to use our second conceptualization of sampling distributions which conceives of sampling distributions in terms of relative frequency distributions. Specifically, the relative frequency distribution that would occur if samples of two balls were repeatedly taken and the mean of each sample computed.
When we have a truly continuous distribution, it is not only impractical but actually impossible to enumerate all possible outcomes. Moreover, in continuous distributions, the probability of obtaining any single value is zero. Therefore, as discussed in the section "Introduction to Distributions," these values are called probability densities rather than probabilities.
Sampling Distributions and Inferential Statistics
As we stated in the beginning of this chapter, sampling distributions are important for inferential statistics. In the examples given so far, a population was specified and the sampling distribution of the mean and the range were determined. In practice, the process proceeds the other way: you collect sample data and from these data you estimate parameters of the sampling distribution. This knowledge of the sampling distribution can be very useful. For example, knowing the degree to which means from different samples would differ from each other and from the population mean would give you a sense of how close your particular sample mean is likely to be to the population mean. Fortunately, this information is directly available from a sampling distribution. The most common measure of how much sample means differ from each other is the standard deviation of the sampling distribution of the mean. This standard deviation is called the standard error of the mean. If all the sample means were very close to the population mean, then the standard error of the mean would be small. On the other hand, if the sample means varied considerably, then the standard error of the mean would be large.
To be specific, assume your sample mean were \(125\) and you estimated that the standard error of the mean were \(5\) (using a method shown in a later section). If you had a normal distribution, then it would be likely that your sample mean would be within \(10\) units of the population mean since most of a normal distribution is within two standard deviations of the mean.
Keep in mind that all statistics have sampling distributions, not just the mean. In later sections we will be discussing the sampling distribution of the variance, the sampling distribution of the difference between means, and the sampling distribution of Pearson's correlation, among others.


