3.15: Shapes of Distributions
- Page ID
- 2309
Learning Objectives
- Compute skew using two different formulas
- Compute kurtosis
We saw in the section on distributions in Chapter 1 that shapes of distributions can differ in skew and/or kurtosis. This section presents numerical indexes of these two measures of shape.
Skew
Figure \(\PageIndex{1}\) shows a distribution with a very large positive skew. Recall that distributions with positive skew have tails that extend to the right.
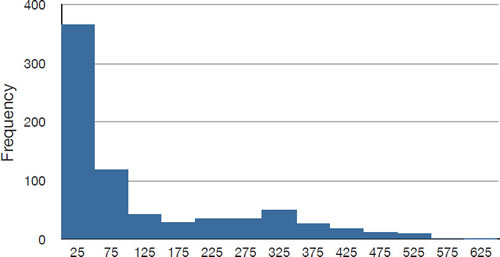
Distributions with positive skew normally have larger means than medians. The mean and median of the baseball salaries shown in Figure \(\PageIndex{1}\) are \(\$1,183,417\) and \(\$500,000\) respectively. Thus, for this highly-skewed distribution, the mean is more than twice as high as the median. The relationship between skew and the relative size of the mean and median led the statistician Pearson to propose the following simple and convenient numerical index of skew:
\[\frac{3(Mean-Median)}{\sigma }\]
The standard deviation of the baseball salaries is \(1,390,922\). Therefore, Pearson's measure of skew for this distribution is \(\dfrac {3(1,183,417 - 500,000)}{1,390,922} = 1.47\).
Just as there are several measures of central tendency, there is more than one measure of skew. Although Pearson's measure is a good one, the following measure is more commonly used. It is sometimes referred to as the third moment about the mean.
\[\sum \dfrac {(X-\mu )^3}{\sigma ^3}\]
Kurtosis
The following measure of kurtosis is similar to the definition of skew. The value "\(3\)" is subtracted to define "no kurtosis" as the kurtosis of a normal distribution. Otherwise, a normal distribution would have a kurtosis of \(3\).
\[\sum \dfrac {(X-\mu )^4}{\sigma ^4}-3\]


