3.10: Comparing Measures
- Page ID
- 2304
Learning Objectives
- State how the measures differ in symmetric distributions
- State which measure(s) should be used to describe the center of a skewed distribution
How do the various measures of central tendency compare with each other? For symmetric distributions, the mean, median, trimean, and trimmed mean are equal, as is the mode except in bimodal distributions. Differences among the measures occur with skewed distributions. Figure \(\PageIndex{1}\) shows the distribution of \(642\) scores on an introductory psychology test. Notice this distribution has a slight positive skew.
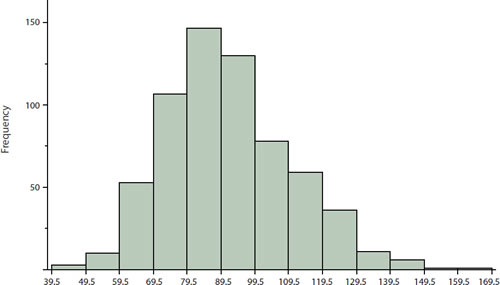
Measures of central tendency are shown in Table \(\PageIndex{1}\). Notice they do not differ greatly, with the exception that the mode is considerably lower than the other measures. When distributions have a positive skew, the mean is typically higher than the median, although it may not be in bimodal distributions. For these data, the mean of \(91.58\) is higher than the median of \(90\). Typically the trimean and trimmed mean will fall between the median and the mean, although in this case, the trimmed mean is slightly lower than the median. The geometric mean is lower than all measures except the mode.
| Measure | Value |
|---|---|
| Mode | 84.00 |
| Median | 90.00 |
| Geometric Mean | 89.70 |
| Trimean | 90.25 |
| Mean Trimmed 50% | 89.81 |
| Mean | 91.58 |
The distribution of baseball salaries (in \(1994\)) shown in Figure \(\PageIndex{2}\) has a much more pronounced skew than the distribution in Figure \(\PageIndex{2}\).
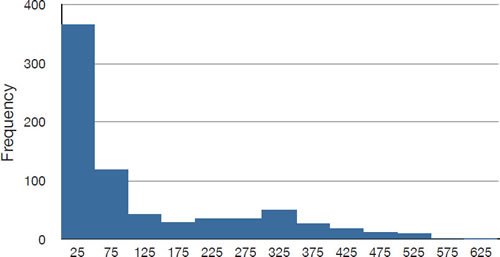
Table \(\PageIndex{2}\) shows the measures of central tendency for these data. The large skew results in very different values for these measures. No single measure of central tendency is sufficient for data such as these. If you were asked the very general question: "So, what do baseball players make?" and answered with the mean of \(\$1,183,000\), you would not have told the whole story since only about one third of baseball players make that much. If you answered with the mode of \(\$250,000\) or the median of \(\$500,000\), you would not be giving any indication that some players make many millions of dollars. Fortunately, there is no need to summarize a distribution with a single number. When the various measures differ, our opinion is that you should report the mean, median, and either the trimean or the mean trimmed \(50\%\). Sometimes it is worth reporting the mode as well. In the media, the median is usually reported to summarize the center of skewed distributions. You will hear about median salaries and median prices of houses sold, etc. This is better than reporting only the mean, but it would be informative to hear more statistics.
| Measure | Value |
|---|---|
| Mode | 250 |
| Median | 500 |
| Geometric Mean | 555 |
| Trimean | 792 |
| Mean Trimmed 50% | 619 |
| Mean | 1,183 |


