2.7.2.5: Interpreting Beyond 2x2 in Graphs
- Page ID
- 22136
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Our graphs so far have focused on the simplest case for factorial designs, the 2x2 design, with two IVs, each with 2 levels. It is worth spending some time looking at a few more complicated designs and how to interpret them. We talked about more complicated designs in the Factorial Notations and Square Tables section, but here's a more focused approach to interpreting the graphs of these advanced designs.
2x3 design
In a 2x3 design there are two IVs. IV1 has two levels, and IV2 has three levels. Typically, there would be one DV. Let’s talk about the main effects and interaction for this design.
First, let’s make the design concrete. Let’s imagine we are running a memory experiment. We give people some words to remember, and then test them to see how many they can correctly remember. Our DV is the proportion (percentage) that participants remembered correctly out of all tries. We know that people forget things over time. Our first IV will be time of test, immediate versus one week later. The time of test IV will produce a forgetting effect. Generally, people will have a higher proportion correct on an immediate test of their memory for things they just saw, compared to testing a week later.
We might be interested in manipulations that reduce the amount of forgetting that happens over the week. Let’s make the second IV the number of time people got to study the items before the memory test, once, twice or three times. We call IV2 the repetition manipulation.
We might expect data that looks like Figure \(\PageIndex{1}\). The top line shows the means when there is no delay (Immediate) for the three levels of repetition. Notice that the proportion correct (y-axis) increases for the Immediate group with each repetition. The bottom ling shows the One Week Delay group over the three levels of repetition. Again, more repetition seems to increase the proportion correct. Let’s talk about this graph in terms of main effects and interaction.
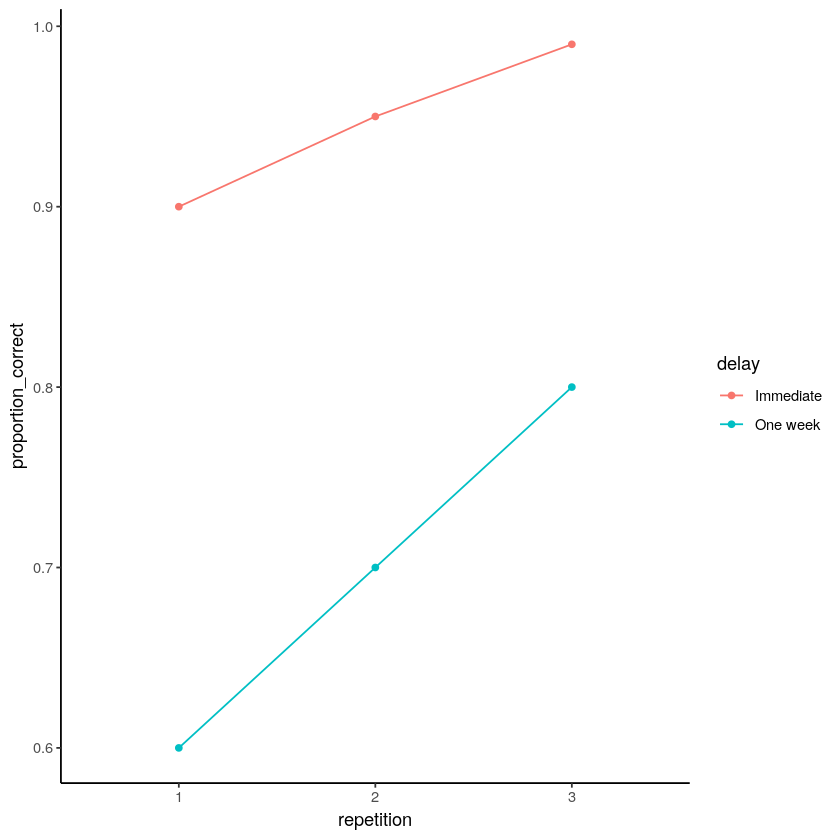
First, the main effect of delay (time of test) is shown by in each differently-colored line, and seems obvious; the red line is on the top, way above the aqua line. This tells us that the proportion correct on the memory test is always higher when the memory test is taken immediately compared to after one week.
Second, the main effect of repetition is presented on the x-axis, and seems to be clearly present. The more times people saw the items in the memory test (once, twice, or three times), the more they remembered, as measured by increasingly higher proportion correct as a function of number of repetitions.
Is there an interaction? Yes, there is. Remember, an interaction occurs when the effect of one IV depends on the levels of an another. The delay IV measures the forgetting effect. Does the size of the forgetting effet change across the levels of the repetition variable? Yes it does. With one repetition the forgetting effect is 0.9 - 0.6 = 0.4. With two repetitions, the forgetting effect is a little bit smaller, and with three, the repetition is even smaller still. So, the size of the forgetting effect changes as a function of the levels of the repetition IV. There is evidence in the means for an interaction. You would have to conduct an inferential test on the interaction term to see if these differences were likely or unlikely to be due to sampling error.
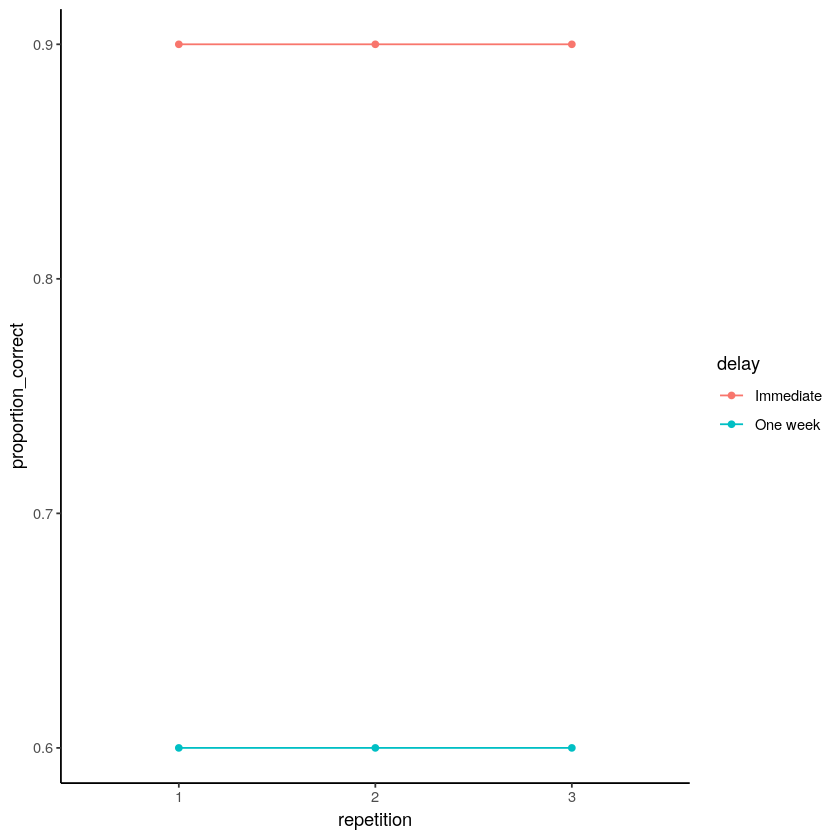
If there was no interaction, and say, no main effect of repetition, we would see something like Figure \(\PageIndex{2}\).
What would you say about the interaction if you saw something like Figure \(\PageIndex{3}\)? The Immediate group is high, but repetition doesn't seem to matter. The One Week Delay group is flat until the third repetition, then increases the proportion correct.
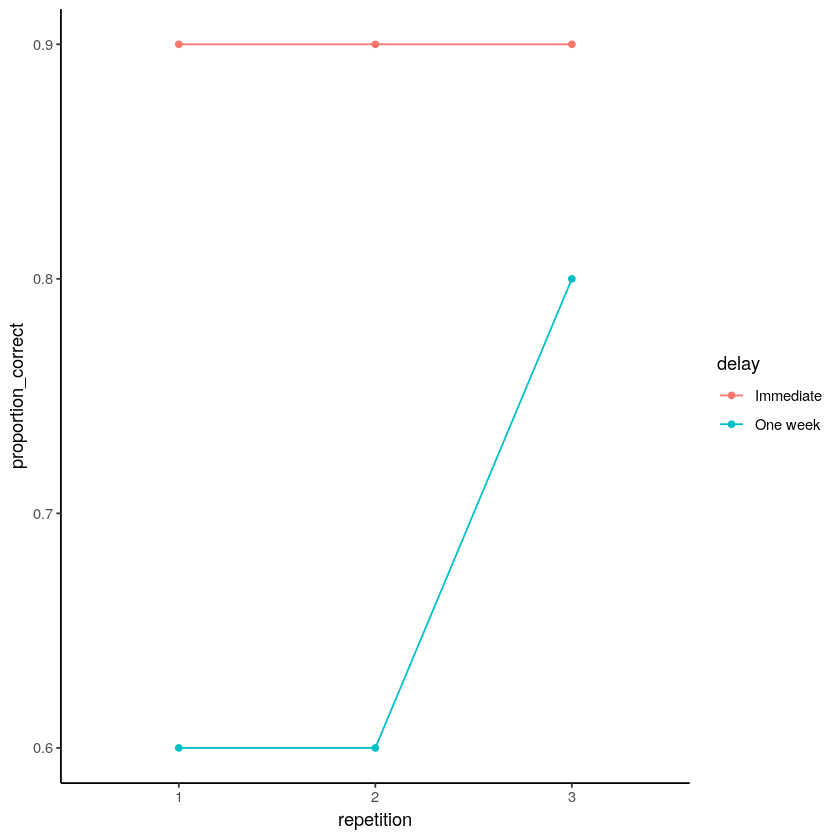
There is evidence in the means for an interaction. Remember, we are measuring the forgetting effect (effect of delay) three times. The forgetting effect is the same for repetition condition 1 and 2, but it is much smaller for repetition condition 3. The size of the forgetting effect depends on the levels of the repetition IV, so here again there is an interaction.
2x2x2 designs
Let’s take it up a notch and look at a 2x2x2 design. Here, there are three IVs with 2 levels each. There are three main effects, three two-way (2x2) interactions, and one 3-way (2x2x2) interaction.
We will use the same example as before but add an additional manipualtion of the kind of material that is to be remembered. For example, we could present words during an encoding phase either visually or spoken (auditory) over headphones.
Figure \(\PageIndex{4}\) shows two pairs of lines, one side (the panel on the left) is for the auditory information to be remembered, and the panel on the right is when the information was presented visually. The lines still show the delay, and the y-axis still shows the number of repetitions. In this version of the study, the was only two repetitions levels: once or twice. The two lines on the left show auditory IV levels and the two lines on the right show visual information. The top lines show when there's no delay, and the diagonal lines show when there is a week delay. There are only two levels of repetition, so there are only two dots representing this IV (1 repetition on the right and 2 repetitions on the left for both auditory and visual information).

You can think of the 2x2x2, as two 2x2s, one for auditory and one for visual. What’s the take home from this example data? We can see that the graphs for auditory and visual are the same. They both show a 2x2 interaction between delay and repetition. People forgot more things across the week when they studied the material once, compared to when they studied the material twice. There is a main effect of delay, there is a main effect of repetition, but there is no main effect of modality (no difference between auditory or visual information), and there is not a three-way interaction.
What is a three-way interaction anyway? That would occur if there was a difference between the 2x2 interactions. For example, consider the next pattern of results (Figure \(\PageIndex{5}\)).

We are looking at a 3-way interaction between modality, repetition and delay in Figure \(\PageIndex{5}\). What is going on here? These results would be very strange, but here is an interpretation.
For auditory stimuli, we see that there is a small forgetting effect when people studied things once, but the forgetting effect gets bigger if they studies things twice. A pattern like this would generally be very strange, usually people would do better if they got to review the material twice.
The visual stimuli show a different pattern. This different pattern is where we get the three-way interaction. Here, the forgetting effect is large when studying visual things once, and it get’s smaller when studying visual things twice.
We see that there is an interaction between delay (the forgetting effect) and repetition for the auditory stimuli; BUT, this interaction effect is different from the interaction effect we see for the visual stimuli. The 2x2 interaction for the auditory stimuli is different from the 2x2 interaction for the visual stimuli. In other words, there is an interaction between the two interactions, as a result there is a three-way interaction, called a 2x2x2 interaction.
We will note a general pattern here. Imagine you had a 2x2x2x2 design. That would have a 4-way interaction. What would that mean? It would mean that the pattern of the 2x2x2 interaction changes across the levels of the 4th IV. If two three-way interactions are different, then there is a four-way interaction.


