5.8: Practice
- Page ID
- 5568
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)5.2 Properties of Continuous Probability Density Functions
1. Which type of distribution does the graph illustrate?
2. Which type of distribution does the graph illustrate?
3. Which type of distribution does the graph illustrate?
4. What does the shaded area represent? \(P\)(___\(< x <\) ___)
5. What does the shaded area represent? \(P\)(___\(< x <\) ___)
6. For a continuous probablity distribution, \(0 \leq x \leq 15\). What is \(P(x > 15)\)?
7. What is the area under \(f(x)\) if the function is a continuous probability density function?
8. For a continuous probability distribution, \(0 \leq x \leq 10\). What is \(P(x = 7)\)?
9. A continuous probability function is restricted to the portion between \(x = 0\) and \(7\). What is \(P(x = 10)\)?
10. \(f(x)\) for a continuous probability function is \(\frac{1}{5}\), and the function is restricted to \(0 \leq x \leq 5\). What is \(P(x < 0)\)?
11. \(f(x)\), a continuous probability function, is equal to \(\frac{1}{12}\), and the function is restricted to \(0 \leq x \leq 12\). What is \(P(0 < x < 12)\)?
12. Find the probability that \(x\) falls in the shaded area.
13. Find the probability that \(x\) falls in the shaded area.
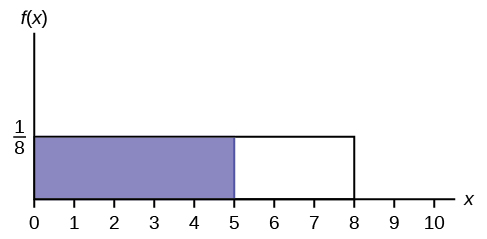.jpg?revision=1)
Figure \(\PageIndex{7}\)
14. Find the probability that \(x\) falls in the shaded area.
15. \(f(x)\), a continuous probability function, is equal to \(\frac{1}{3}\) and the function is restricted to \(1 \leq x \leq 4\). Describe \(P(x>\frac{3}{2})\).
5.3 The Uniform Distribution
Use the following information to answer the next ten questions. The data that follow are the square footage (in 1,000 feet squared) of 28 homes.
| 1.5 | 2.4 | 3.6 | 2.6 | 1.6 | 2.4 | 2.0 |
| 3.5 | 2.5 | 1.8 | 2.4 | 2.5 | 3.5 | 4.0 |
| 2.6 | 1.6 | 2.2 | 1.8 | 3.8 | 2.5 | 1.5 |
| 2.8 | 1.8 | 4.5 | 1.9 | 1.9 | 3.1 | 1.6 |
The sample mean = 2.50 and the sample standard deviation = 0.8302.
The distribution can be written as \(X \sim U(1.5, 4.5)\).
16. What type of distribution is this?
17. In this distribution, outcomes are equally likely. What does this mean?
18. What is the height of \(f(x)\) for the continuous probability distribution?
19. What are the constraints for the values of \(x\)?
20. Graph \(P(2 < x < 3)\).
21. What is \(P(2 < x < 3)\)?
22. What is \(P(x < 3.5 | x < 4)\)?
23. What is \(P(x = 1.5)\)?
24. Find the probability that a randomly selected home has more than 3,000 square feet given that you already know the house has more than 2,000 square feet.
Use the following information to answer the next eight exercises. A distribution is given as \(X \sim U(0, 12)\).
25. What is \(a\)? What does it represent?
26. What is \(b\)? What does it represent?
27. What is the probability density function?
28. What is the theoretical mean?
29. What is the theoretical standard deviation?
30. Draw the graph of the distribution for \(P(x > 9)\).
31. Find \(P(x > 9)\).
Use the following information to answer the next eleven exercises. The age of cars in the staff parking lot of a suburban college is uniformly distributed from six months (0.5 years) to 9.5 years.
32. What is being measured here?
33. In words, define the random variable \(X\).
34. Are the data discrete or continuous?
35. The interval of values for \(x\) is ______.
36. The distribution for \(X\) is ______.
37. Write the probability density function.
38. Graph the probability distribution.
- Sketch the graph of the probability distribution.
Figure \(\PageIndex{9}\) - Identify the following values:
- Lowest value for \(\overline{x}\): _______
- Highest value for \(\overline{x}\): _______
- Height of the rectangle: _______
- Label for x-axis (words): _______
- Label for y-axis (words): _______
39. Find the average age of the cars in the lot.
40. Find the probability that a randomly chosen car in the lot was less than four years old.
- Sketch the graph, and shade the area of interest.
Figure \(\PageIndex{10}\) - Find the probability. \(P(x < 4)\) = _______
41. Considering only the cars less than 7.5 years old, find the probability that a randomly chosen car in the lot was less than four years old.
- Sketch the graph, shade the area of interest.
Figure \(\PageIndex{11}\) - Find the probability. \(P(x < 4 | x < 7.5) =\) _______
42. What has changed in the previous two problems that made the solutions different?
43. Find the third quartile of ages of cars in the lot. This means you will have to find the value such that \(\frac{3}{4}\), or 75%, of the cars are at most (less than or equal to) that age.
- Sketch the graph, and shade the area of interest.
Figure \(\PageIndex{12}\)
- Find the value \(k\) such that \(P(x < k) = 0.75\).
- The third quartile is _______
5.4 The Exponential Distribution
Use the following information to answer the next ten exercises. A customer service representative must spend different amounts of time with each customer to resolve various concerns. The amount of time spent with each customer can be modeled by the following distribution: \(X \sim Exp(0.2)\)
44. What type of distribution is this?
45.Are outcomes equally likely in this distribution? Why or why not?
46. What is \(m\)? What does it represent?
47. What is the mean?
48. What is the standard deviation?
49. State the probability density function.
50. Graph the distribution.
51. Find \(P(2 < x < 10)\).
52. Find \(P(x > 6)\).
53. Find the 70th percentile.
Use the following information to answer the next seven exercises. A distribution is given as \(X \sim Exp(0.75)\).
54. What is m?
55. What is the probability density function?
56. What is the cumulative distribution function?
57. Draw the distribution.
58. Find \(P(x < 4)\).
59. Find the 30th percentile.
60. Find the median.
61. Which is larger, the mean or the median?
Use the following information to answer the next 16 exercises. Carbon-14 is a radioactive element with a half-life of about 5,730 years. Carbon-14 is said to decay exponentially. The decay rate is 0.000121. We start with one gram of carbon-14. We are interested in the time (years) it takes to decay carbon-14.
62. What is being measured here?
63. Are the data discrete or continuous?
64. In words, define the random variable \(X\).
65. What is the decay rate (\(m\))?
66. The distribution for \(X\) is ______.
67. Find the amount (percent of one gram) of carbon-14 lasting less than 5,730 years. This means, find \(P(x < 5,730)\).
- Sketch the graph, and shade the area of interest.
Figure \(\PageIndex{13}\) - Find the probability. \(P(x < 5,730) =\) __________
68. Find the percentage of carbon-14 lasting longer than 10,000 years.
- Sketch the graph, and shade the area of interest.
Figure \(\PageIndex{14}\) - Find the probability. \(P(x > 10,000) =\) ________
69. Thirty percent (30%) of carbon-14 will decay within how many years?
- Sketch the graph, and shade the area of interest.
Figure \(\PageIndex{15}\) Find the value \(k\) such that \(P(x < k) = 0.30\).


