10.15: Distribution of Sample Means (3 of 4)
- Page ID
- 14182
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Describe the sampling distribution of sample means.
Shape of the Sampling Distribution of Means
Now we investigate the shape of the sampling distribution of sample means. When we discussed the sampling distribution of sample proportions, we learned that this distribution is approximately normal if np ≥ 10 and n(1 – p) ≥ 10. In other words, we had a guideline based on sample size for determining the conditions under which we could use a normal curve to do probability calculations for sample proportions.
Now we investigate these questions:
- When will the distribution of sample means be approximately normal?
- Does it depend on the size of the sample?
- What happens if the distribution of the variable in the population is heavily skewed?
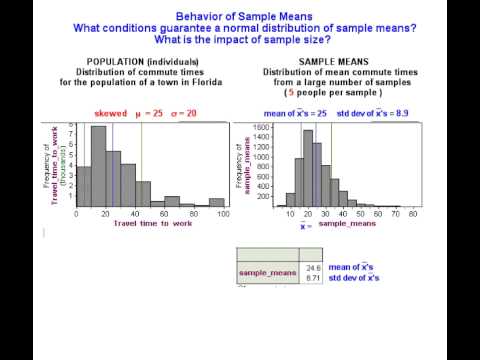
The following simulation video helps us investigate these questions.
WalkThrough Simulation
Comment
Are you surprised that a variable with a skewed distribution in the population can have a sampling distribution that is approximately normal? This discovery is probably the single most important result presented in introductory statistics courses. It is called the central limit theorem, which says that for large samples, the sampling distribution of sample means is approximately normal. This theorum is important! Inference procedures, such as hypothesis tests and confidence intervals, are based on a normal model for the sampling distribution. The central limit theorem assures us that we can use a normal probability model for sample means without knowing anything about the shape of the distribution of the variable in the population. All we have to do is collect large samples.
How large a sample size do we need to assume that sample means will be normally distributed? It really depends on the population distribution, as we saw in the simulation. The more skewed the distribution in the population, the larger the samples we need in order to use a normal model for the sampling distribution.
The general guideline is that samples of size greater than 30 will have a fairly normal distribution regardless of the shape of the distribution of the variable in the population. But if a population is strongly skewed, it is safer to use larger samples.
Try It
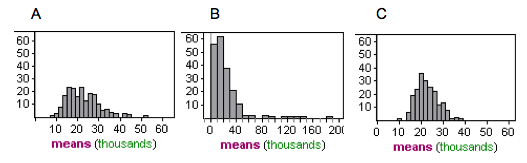
The distribution of incomes is strongly skewed to the right for individuals in the U.S. The following histograms represent mean income from 200 samples randomly selected from the U.S. population. One histogram is based on samples of size of n = 4, one on samples of size of n = 40, and one on samples of size of n = 100.
Summary
- Let’s say we have a quantitative data set from a population with mean μ and standard deviation σ.The model for the theoretical sampling distribution of means of all random samples of size n has the following properties:
- The mean of the sampling distribution of means is μ.
- The standard deviation of the sampling distribution of means is
.
- Notice that as n grows, the standard deviation of the sampling distribution of means shrinks.
- For large enough sample size, the sampling distribution of means is approximately normal (even if population is not normal).
- If a variable has a skewed distribution for individuals in the population, a larger sample size is needed to ensure that the sampling distribution has a normal shape.
- The general rule is that if n is more than 30, then the sampling distribution of means will be approximately normal. However, if the population is already normal, then any sample size will produce a normal sampling distribution.
Comment
Notice that the size of the population is not mentioned in our discussion of sampling distributions. From our discussion, we know the following:
- The means from larger samples have less variability, so larger samples give more accurate estimates of the population mean.
- The means from larger samples have a distribution with a shape that is closer to normal.
These statements are true regardless of the size of the population as long as the population is large. To illustrate this point, we compare a distribution of sample means from two populations of different sizes. Population A has 10,000 newborns. Population B has 20,000 newborns. For each population, the mean and standard deviation of individual birth weights is the same: μ = 3,500 and σ = 500.
We selected 525 random samples of 100 babies from each population and made a histogram of the sample means. We did this twice for population A, so two of the histograms represent 525 samples from the same population. As expected, there are some differences in the samples collected due to random chance. Comparing these two histograms gives us a sense of how much variation we can expect from the process of selecting random samples. Notice that the histogram of sample means from the larger population B has a similar shape, center, and spread to the histograms from population A.

What’s the Main Point?
The size of the population does not affect the variability of the sample means. Size matters if we are talking about sample size for random samples, but size does not matter if we are talking about population size as long as the population is large.
Contributors and Attributions
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution