9.17: Hypothesis Test for Difference in Two Population Proportions (4 of 6)
- Page ID
- 14144
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Under appropriate conditions, conduct a hypothesis test for comparing two population proportions or two treatments. State a conclusion in context.
- Given the description of a statistical study, evaluate whether conclusions are reasonable.
Reminder about Finding P-values
In a hypothesis test, the P-value is based on the assumption that the null hypothesis is true. But the P-value is also related to the alternative hypothesis. The logic here is the same logic we used in Inference for One Proportion with hypothesis tests.
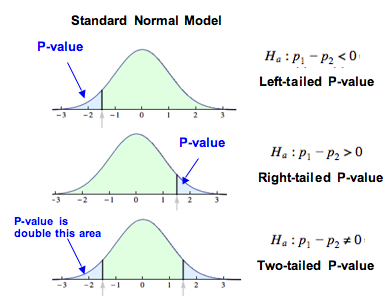
When Ha: p1 − p2 < 0, the difference in sample proportions from the data must be significantly less than zero to provide evidence against the null hypothesis and in favor of the alternative hypothesis. In this case, the P-value describes differences in sample proportions that are less than the difference observed in the data. This is the area to the left of the test statistic. We call it a left-tailed test.
Similarly, when Ha: p1 − p2 > 0, the difference in sample proportions observed in the data must be significantly greater than zero to provide evidence against the null hypothesis and in favor of the alternative hypothesis. In this case, the P-value describes differences in sample proportions that are greater than the difference observed in the data. This is the area to the right of the test statistic. We call it a right-tailed test.
When Ha: p1 − p2 ≠ 0, the difference in sample proportions observed in the data must be significantly different from zero to provide evidence against the null hypothesis and in favor of the alternative hypothesis. In this case, the P-value is two-tailed. It is twice the area of the smaller tail defined by the test statistic.
The next two activities provide more practice with conducting a hypothesis test for a difference between two population proportions. You will need the simulation below to complete these activities.
Click here to open this simulation in its own window.
Try It
Is a New Antidepressant Effective in Treating Depression?
Depression has many effective treatment options. Suppose that in a clinical trial researchers study a new antidepressant. They randomly assign 90 depressed teens to one of two groups: 40 teens receive the antidepressant Fluoxetine with psychiatric therapy. Of these, 25 improve. The remaining 50 teens receive placebos with psychiatric therapy. Among this group, 18 improve. The experiment is double blind, so neither the teens nor the psychiatrists know which participants receive Fluoxetine or placebo.
Define p1 and p2 to be the proportions of all teens who improve when taking Fluoxetine and placebo, respectively, with psychiatric treatment. We will test the claim, at 1% significance (α = 0.01), that the proportion of teens who improve after the Fluoxetine treatment is greater than the proportion for teens who received a placebo.
https://assessments.lumenlearning.co...sessments/3648
https://assessments.lumenlearning.co...sessments/3942
Try It
Are There Racial Differences in Antidepressant Use?
The following excerpt is from an article by Kerry Sheridan, “In the US, Many with Severe Depression Go Untreated” (AFP, Oct. 19, 2011).
- The United States is a world leader in rates of antidepressant use, but as many as two-thirds of Americans with severe depression are not on medication….The data also showed significant racial and ethnic differences, with almost 14 percent of non-Hispanic whites taking antidepressants compared to four percent of African-Americans and three percent of Mexican-Americans….[E]ven though non-whites are getting treated less often, studies have shown that they are just as likely as whites to suffer from depression. Income appeared to play no role in the prevalence of antidepressant usage, said the study.
The data in this study comes from 12,637 people who were interviewed as part of the National Health and Nutrition Examination Surveys (NHAMES) from 2005 to 2008.
https://assessments.lumenlearning.co...sessments/3943
https://assessments.lumenlearning.co...sessments/3944
Contributors and Attributions
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution

