3.26: Causation and Lurking Variables (2 of 2)
- Page ID
- 14038
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Distinguish between association and causation. Identify lurking variables that may explain an observed relationship.
In the next example, we investigate a subtle point about the confusion between association and causation. In this example, a cause-and-effect connection is logical but not justified by an observed association in a single study.
Example
Smoking and Lung Cancer
In this data, x = cigarette consumption per capita in the United States, and y = lung cancers per 100,000. To investigate the connection between cigarette consumption and lung cancers, the data is offset by 30 years because cancer takes time to develop. For example, cigarette consumption in 1945 is paired with cancer rates for 1975.
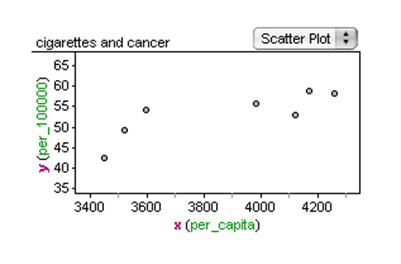
In the scatterplot, we see a fairly strong positive correlation.
Can we conclude from this data that cigarette smoking causes lung cancer? The answer is no.
The data comes from an observational study. Recall from our previous discussions in Module 1 that we can draw cause-and-effect conclusions only from randomized comparative experiments. From this study, we can say that cigarette smoking is associated with lung cancer. We can also say that cigarette smoking correlates with lung cancer. We cannot say that cigarette smoking causes lung cancer.
Yet the National Cancer Institute’s website states that “cigarette smoking causes many types of cancer, including cancers of the lung” (National Cancer Institute).
How can this be? Did the National Cancer Institute conduct a randomized comparative experiment to establish this cause-and-effect relationship? Of course not. We cannot randomly assign people to smoke or not smoke. All of the studies linking smoking with cancer are observational studies. Alone, each study can show only an association.
So is it possible to draw a causal link between cigarette consumption and cancer rates? The answer is yes, well sort of. In practice, researchers use criteria such as the following to provide evidence of a causal connection from observational studies:
- There is a reasonable explanation for how one variable might cause the other.
- The association is seen in repeated studies under varying conditions.
- The effects of potential lurking variables are ruled out when we look across studies.
The point of the previous example is again that association does not imply causation. But researchers can use an observed association as the first step in building a case for causation.
This point is subtle but important. When experiments cannot be conducted, it can be difficult and controversial to explain an observed association between two variables. Many of the current disputes involving data and statistics involve questions of causation that we cannot investigate through an experiment. Does the death penalty reduce violent crime? Does cell phone use cause brain tumors? Does pollution cause global warming? All of these questions imply a cause-and-effect relationship in situations that are complex and involve many interacting variables. In these situations, a single observational study cannot establish a causal link between two variables. But researchers can use the observed association as a first step in building a case for causation.
Let’s Summarize
- The relationship between two quantitative variables is visually displayed using the scatterplot, where each point represents an individual. We always plot the explanatory variable on the horizontal axis and the response variable on the vertical axis.
- When we explore a relationship using the scatterplot, we should describe the overall pattern of the relationship and any deviations from that pattern. To describe the overall pattern, consider the direction, form, and strength of the relationship.
- Adding labels to the scatterplot that indicate different groups or categories within the data might help us gain more insight about the relationship we are exploring.
- A special case of the relationship between two quantitative variables is the linear relationship. In this case, a straight line simply and adequately summarizes the relationship.
- When the scatterplot displays a linear relationship, we supplement it with the correlation coefficient (r), which measures the strength and the direction of a linear relationship between two quantitative variables. The correlation ranges between -1 and 1. Values near -1 indicate a strong negative linear relationship. Values near 0 can indicate a weak or no linear relationship. Values near 1 indicate a strong positive linear relationship. Remember, we use the correlation coefficient only after we have looked at the data and observed that there is a linear relationship. If you have no information about what the data actually looks like, then you should not use the correlation coefficient in your analysis.
- The correlation is an appropriate numerical measure only for linear relationships, and it is sensitive to outliers. Therefore, the correlation should be used only as a supplement to a scatterplot (after we look at the data).
- A lurking variable is a variable that is not measured in the study. It is a third variable that is neither the explanatory nor the response variable, but it affects your interpretation of the relationship between the explanatory and response variable.
- Association does not imply causation. Do not interpret a high correlation between explanatory and response variables as a cause-and-effect relationship.
- An observational study alone cannot establish a causal connection between explanatory and response variables. To establish a cause-and-effect relationship, researchers must conduct a comparative randomized experiment. In reality, it is often impossible to conduct an experiment. So observational studies that show an association between two variables can be used as a first step in building a case for causation.
Contributors and Attributions
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution

