1.11: Conducting Experiments (1 of 2)
- Page ID
- 13992
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Identify features of experiment design that control the effects of confounding.
We now focus on experiments.
The primary goal of an experiment is to provide evidence for a cause-and-effect relationship between two variables. An experiment intentionally manipulates the explanatory variable in an attempt to cause an effect on the response variable. To establish a cause-and-effect relationship, we want to make sure that the explanatory variable is the only factor that impacts the response variable. We therefore attempt to get rid of all other factors that might affect the response. These other factors are called confounding variables.
To confound means to mix up or to confuse. Confounding variables mix up our ability to determine if the explanatory variable causes a change in the response variable. If we do not control the effects of confounding variables, the experiment does not provide evidence of a cause-and-effect relationship between the explanatory and response variables.
Researchers use two common strategies to control the effects of confounding variables:
- Direct control
- Random assignment
Example
Direct Control
Researchers compare bacteria reduction for three different hand-drying methods. In this experiment, participants handled uncooked chicken for 45 seconds, then washed their hands with one squirt of soap for 60 seconds, and then used one of three hand-drying methods. After participants completely dried their hands, researchers measured the bacteria count on their hands. The Infectious Disease News published the results in 2010.
In this experiment, the explanatory variable is hand-drying method.The response variable is bacteria count. Notice that the explanatory variable determines the three treatments in the experiment. Each treatment is a different hand-drying method. For this reason, the explanatory variable is also called the treatment variable.
In this experiment, researchers attempt to directly control the influence of three variables that could affect the bacteria count:
(1) Length of time participants handle the raw chicken.
- Direct control: All participants handle the raw chicken for 45 seconds.
(2) Amount of soap participants use.
- Direct control: All participants use one squirt of soap.
(3) Amount of time participants wash hands.
- Direct control: All participants wash their hands for 60 seconds.
Notice that the control works by stabilizing the impact of the confounding variable across the treatments. For example, the amount of soap will still influence the bacteria count. We cannot avoid this. But if all participants use the same amount of soap, then differences in bacteria count among the three treatments cannot be due to the amount of soap used.
Similarly, the amount of time that participants wash their hands will influence the bacteria count. But if all participants wash their hands for the same amount of time, then differences in bacteria count among the three treatments cannot be due to the amount of time participants washed their hands. This is what we mean when we say that the control works by stabilizing the impact of the confounding variable across the treatments.
Now we examine random assignment. Random assignment controls the effects of confounding variables that a researcher cannot control directly or that are difficult to identify in advance.
Example
Random Assignment
Medical researchers conducted an experiment to compare two different types of surgery for children with hernias. They compared the recovery times for each type of surgery. The two surgery types are laparoscopic repair (a surgery that involves three small incisions) and open repair (a surgery that involves one large incision). Researchers identified a variety of variables that might influence recovery time, such as child’s age, weight, and physical fitness level.
Let’s consider one of these variables: age. How could the researchers control the impact of age on recovery time?
Direct control involves use of children of the same age. For example, researchers might use only 10-year-old children in the experiment. But it may be difficult to find enough 10-year-old children with hernias. So how do researchers create treatment groups that are similar with respect to age? One way is to assign children at random to treatment groups.
The goal of random assignment is to create similar groups with respect to age, weight, and other characteristics that might influence recovery time. To illustrate how random assignment creates similar groups, we focus on age. Here is a dotplot of the ages of the 48 children with hernias who participated in this experiment. Each dot represents a child. The average age of the 48 children is 8.29 years.
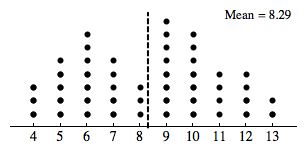
If random assignment is working, the average age for each treatment group should be about equal. We see how random assignment works in the next activity.
Click Random Assignment to randomly assign the 48 children to the two treatments. Repeat this process several times to investigate whether random assignment creates groups with similar ages. The average age is labeled as the mean and marked with a vertical line. Compare the average ages for the treatment groups.
Click here to open this simulation in its own window.
What Is the Main Point?
The goal of random assignment is to create similar treatment groups. If the groups are similar, then any differences we see in the response variable are due to the differences in treatments. In this way, random assignment controls the impact of confounding variables. Random assignment in an experiment eliminates confounding, just as random selection in a survey eliminates bias.
Comment
How do we make random assignments? We use any method that allows random chance to choose the treatment for each participant. Random assignment means that each participant has an equal chance of receiving any one of the treatment options. For example, in the hernia experiment, you could put every child’s name in a hat. The first 24 names drawn get the first treatment. The rest of the children get the second treatment. You could also flip a coin. Heads means the child is assigned to the first treatment. This method could create groups with slightly different sizes, which is fine.
Try It
The following paragraph is from a 1999 USA Today article titled “Heart care reflects race and sex, not symptoms.”
“Previous research suggested that blacks and women were less likely than whites and men to get cardiac catheterization or coronary bypass surgery for chest pain or a heart attack. Scientists blamed differences in illness severity, insurance coverage, patient preference, and health care access. The researchers eliminated those differences by videotaping actors – two black men, two white men, two black women, two white women – describing chest pain from identical scripts. They wore identical gowns, used identical hand gestures, and were taped from the same position. Researchers asked 720 primary care doctors at meetings of the American College of Physicians or the American Academy of Family Physicians to watch a tape and recommend care. The doctors thought the study focused on clinical decision making.”
Researchers rolled a four-sided die to determine which video each doctor watched.
https://assessments.lumenlearning.co...sessments/3409
https://assessments.lumenlearning.co...sessments/3410
Contributors and Attributions
- Concepts in Statistics. Provided by: Open Learning Initiative. Located at: http://oli.cmu.edu. License: CC BY: Attribution

