4.4: Binomial Distribution
- Page ID
- 20366
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The binomial distribution is frequently used to model the number of successes in a sample of size \(n\) drawn with replacement from a population of size \(N\).
Three characteristics of a binomial experiment
- There are a fixed number of trials. Think of trials as repetitions of an experiment. The letter \(n\) denotes the number of trials.
- There are only two possible outcomes, called "success" and "failure," for each trial. The letter \(p\) denotes the probability of a success on one trial, and \(q\) denotes the probability of a failure on one trial. \(p + q = 1\).
- The \(n\) trials are independent and are repeated using identical conditions. Because the \(n\) trials are independent, the outcome of one trial does not help in predicting the outcome of another trial. Another way of saying this is that for each individual trial, the probability, \(p\), of a success and probability, \(q\), of a failure remain the same. For example, randomly guessing at a true-false statistics question has only two outcomes. If a success is guessing correctly, then a failure is guessing incorrectly. Suppose Joe always guesses correctly on any statistics true-false question with probability \(p = 0.6\). Then, \(q = 0.4\). This means that for every true-false statistics question Joe answers, his probability of success (\(p = 0.6\)) and his probability of failure (\(q = 0.4\)) remain the same.
The outcomes of a binomial experiment fit a binomial probability distribution. The random variable \(X =\) the number of successes obtained in the \(n\) independent trials. The mean, \(\mu\), and variance, \(\sigma^{2}\), for the binomial probability distribution are
\[\mu = np\]
and
\[\sigma^{2} = npq.\]
The standard deviation, \(\sigma\), is then
\[\sigma = \sqrt{npq}.\]
Any experiment that has characteristics two and three and where \(n = 1\) is called a Bernoulli Trial (named after Jacob Bernoulli who, in the late 1600s, studied them extensively). A binomial experiment takes place when the number of successes is counted in one or more Bernoulli Trials.
Example \(\PageIndex{1}\)
At ABC College, the withdrawal rate from an elementary physics course is 30% for any given term. This implies that, for any given term, 70% of the students stay in the class for the entire term. A "success" could be defined as an individual who withdrew. The random variable \(X =\) the number of students who withdraw from the randomly selected elementary physics class.
Exercise \(\PageIndex{1}\)
The state health board is concerned about the amount of fruit available in school lunches. Forty-eight percent of schools in the state offer fruit in their lunches every day. This implies that 52% do not. What would a "success" be in this case?
Answer
a school that offers fruit in their lunch every day
Example \(\PageIndex{2}\)
Suppose you play a game that you can only either win or lose. The probability that you win any game is 55%, and the probability that you lose is 45%. Each game you play is independent. If you play the game 20 times, write the function that describes the probability that you win 15 of the 20 times. Here, if you define \(X\) as the number of wins, then \(X\) takes on the values 0, 1, 2, 3, ..., 20. The probability of a success is \(p = 0.55\). The probability of a failure is \(q = 0.45\). The number of trials is \(n = 20\). The probability question can be stated mathematically as \(P(x = 15)\).
Exercise \(\PageIndex{2}\)
A trainer is teaching a dolphin to do tricks. The probability that the dolphin successfully performs the trick is 35%, and the probability that the dolphin does not successfully perform the trick is 65%. Out of 20 attempts, you want to find the probability that the dolphin succeeds 12 times. State the probability question mathematically.
Answer
\(P(x = 12)\)
Example \(\PageIndex{3}\)
A fair coin is flipped 15 times. Each flip is independent. What is the probability of getting more than ten heads? Let \(X =\) the number of heads in 15 flips of the fair coin. \(X\) takes on the values 0, 1, 2, 3, ..., 15. Since the coin is fair, \(p = 0.5\) and \(q = 0.5\). The number of trials is \(n = 15\). State the probability question mathematically.
Solution
\(P(x > 10)\)
Exercise \(\PageIndex{4}\)
A fair, six-sided die is rolled ten times. Each roll is independent. You want to find the probability of rolling a one more than three times. State the probability question mathematically.
Answer
\(P(x > 3)\)
Example \(\PageIndex{5}\)
Approximately 70% of statistics students do their homework in time for it to be collected and graded. Each student does homework independently. In a statistics class of 50 students, what is the probability that at least 40 will do their homework on time? Students are selected randomly.
- This is a binomial problem because there is only a success or a __________, there are a fixed number of trials, and the probability of a success is 0.70 for each trial.
- If we are interested in the number of students who do their homework on time, then how do we define \(X\)?
- What values does \(x\) take on?
- What is a "failure," in words?
- If \(p + q = 1\), then what is \(q\)?
- The words "at least" translate as what kind of inequality for the probability question \(P(x\) ____ \(40\)).
Solution
- failure
- \(X\) = the number of statistics students who do their homework on time
- 0, 1, 2, …, 50
- Failure is defined as a student who does not complete his or her homework on time. The probability of a success is \(p = 0.70\). The number of trials is \(n = 50\).
- \(q = 0.30\)
- greater than or equal to (\(\geq\)). The probability question is \(P(x \geq 40)\).
Exercise \(\PageIndex{5}\)
Sixty-five percent of people pass the state driver’s exam on the first try. A group of 50 individuals who have taken the driver’s exam is randomly selected. Give two reasons why this is a binomial problem.
Answer
This is a binomial problem because there is only a success or a failure, and there are a definite number of trials. The probability of a success stays the same for each trial.
Notation for the Binomial: \(B =\) Binomial Probability Distribution Function
\[X \sim B(n, p)\]
Read this as "\(X\) is a random variable with a binomial distribution." The parameters are \(n\) and \(p\); \(n =\) number of trials, \(p =\) probability of a success on each trial.
Binomial Distribution calculator
Enter the lower bound for the number of successes (Low), the upper bound for the number of successes (Up), the number of trials (Trials), and the probability of success (P), and then hit Calculate.
| Low: | Up: | Trials: | P: |
Example \(\PageIndex{6}\)
It has been stated that about 41% of adult workers have a high school diploma but do not pursue any further education. If 20 adult workers are randomly selected, find the probability that at most 12 of them have a high school diploma but do not pursue any further education. How many adult workers do you expect to have a high school diploma but do not pursue any further education?
Let \(X\) = the number of workers who have a high school diploma but do not pursue any further education.
\(X\) takes on the values 0, 1, 2, ..., 20 where \(n = 20, p = 0.41\), and \(q = 1 – 0.41 = 0.59\). \(X \sim B(20, 0.41)\)
Find \(P(x \leq 12)\). \(P(x \leq 12) = 0.9738\). (calculator or computer)
Low = 0, High = 12, Trials = 20, p = 0.41
The graph of \(X \sim B(20, 0.41)\) is as follows:
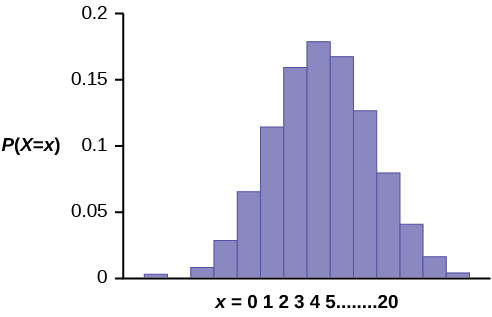
The y-axis contains the probability of \(x\), where \(X =\) the number of workers who have only a high school diploma.
The number of adult workers that you expect to have a high school diploma but not pursue any further education is the mean, \(\mu = np = (20)(0.41) = 8.2\).
The formula for the variance is \(\sigma^{2} = npq\). The standard deviation is \(\sigma = \sqrt{npq}\).
\[\sigma = \sqrt{(20)(0.41)(0.59)} = 2.20.\]
Query \(\PageIndex{1}\)
Exercise 4.4.5
About 32% of students participate in a community volunteer program outside of school. If 30 students are selected at random, find the probability that at most 14 of them participate in a community volunteer program outside of school. Use the LibreTexts calculator to find the answer.
Answer
\(P(x \leq 14) = 0.9695\)
Example \(\PageIndex{7}\)
In the 2013 Jerry’s Artarama art supplies catalog, there are 560 pages. Eight of the pages feature signature artists. Suppose we randomly sample 100 pages. Let \(X =\) the number of pages that feature signature artists.
- What values does \(x\) take on?
- What is the probability distribution? Find the following probabilities:
- the probability that two pages feature signature artists
- the probability that at most six pages feature signature artists
- the probability that more than three pages feature signature artists.
- Using the formulas, calculate the (i) mean and (ii) standard deviation.
Answer
- \(x = 0, 1, 2, 3, 4, 5, 6, 7, 8\)
- \(X \sim B(100,8560)(100,8560)\) Use the Binomial Calculator:
- Low = 2, High = 2, Trials = 100, p = \(\dfrac{8}{560} = 0.01429, P(x = 2) = 0.2466\)
- Low = 0, High = 6, Trials = 100, p = \(\dfrac{8}{560} = 0.01429, P(x \leq 6) = 0.9994\)
- Low = 4, High = 100, Trials = 100, p = \(\dfrac{8}{560} = 0.01429, P(x > 3) = 0.0557\)
-
- Mean \(= np = (100)\left(\dfrac{8}{560}\right) = \dfrac{800}{560} \approx 1.4286\)
- Standard Deviation \(= \sqrt{npq} = \sqrt{(100)\left(\dfrac{8}{560}\right)\left(\dfrac{552}{560}\right)} \approx 1.1867\)
Query \(\PageIndex{1}\)
Exercise \(\PageIndex{7}\)
According to a Gallup poll, 60% of American adults prefer saving over spending. Let \(X\) = the number of American adults out of a random sample of 50 who prefer saving to spending.
- What is the probability distribution for \(X\)?
- Use your calculator to find the following probabilities:
- the probability that 25 adults in the sample prefer saving over spending
- the probability that at most 20 adults prefer saving
- the probability that more than 30 adults prefer saving
- Using the formulas, calculate the (i) mean and (ii) standard deviation of \(X\).
Answer
- \(X \sim B(50, 0.6)\)
- Using the LibreTexts calculator:
- \(P(x = 25) = 0.0405\)
- \(P(x \leq 20) = 0.0034\)
- \(P(x > 30) = 0.4465\)
-
- Mean \(= np = 50(0.6) = 30\)
- Standard Deviation \(= \sqrt{npq} = \sqrt{50(0.6)(0.4)} \approx 3.4641\)
Query \(\PageIndex{1}\)
Example \(\PageIndex{8}\)
The lifetime risk of developing pancreatic cancer is about one in 78 (1.28%). Suppose we randomly sample 200 people. Let \(X\) = the number of people who will develop pancreatic cancer.
- What is the probability distribution for \(X\)?
- Using the formulas, calculate the (i) mean and (ii) standard deviation of \(X\).
- Use your calculator to find the probability that at most eight people develop pancreatic cancer
- Is it more likely that five or six people will develop pancreatic cancer? Justify your answer numerically.
Answer
- \(X \sim B(200, 0.0128)\)
-
- Mean \(= np = 200(0.0128) = 2.56\)
- Standard Deviation \(= \sqrt{npq} = \sqrt{(200)(0.0128)(0.9872)} \approx 1.5897\)
- Using the LibreTexts calculator:
\(P(x \leq 8) = 0.9988\) - \(P(x = 5) = 0.0707\)
\(P(x = 6) = 0.0298\)
So \(P(x = 5) > P(x = 6)\); it is more likely that five people will develop cancer than six.
Exercise \(\PageIndex{8}\)
During the 2013 regular NBA season, DeAndre Jordan of the Los Angeles Clippers had the highest field goal completion rate in the league. DeAndre scored with 61.3% of his shots. Suppose you choose a random sample of 80 shots made by DeAndre during the 2013 season. Let \(X =\) the number of shots that scored points.
- What is the probability distribution for \(X\)?
- Using the formulas, calculate the (i) mean and (ii) standard deviation of \(X\).
- Use your calculator to find the probability that DeAndre scored with 60 of these shots.
- Find the probability that DeAndre scored with more than 50 of these shots.
Answer
- \(X \sim B(80, 0.613)\)
-
- Mean \(= np = 80(0.613) = 49.04\)
- Standard Deviation \(= \sqrt{npq} = \sqrt{80(0.613)(0.387)} \approx 4.3564\)
- Using the LibreTexts calculator:
\(P(x = 60) = 0.0036\) - \(P(x > 50) = 0.3718\)
Example \(\PageIndex{9}\)
The following example illustrates a problem that is not binomial. It violates the condition of independence. ABC College has a student advisory committee made up of ten staff members and six students. The committee wishes to choose a chairperson and a recorder. What is the probability that the chairperson and recorder are both students? The names of all committee members are put into a box, and two names are drawn without replacement. The first name drawn determines the chairperson and the second name the recorder. There are two trials. However, the trials are not independent because the outcome of the first trial affects the outcome of the second trial. The probability of a student on the first draw is \(\dfrac{6}{16}\). The probability of a student on the second draw is \(\dfrac{5}{15}\), when the first draw selects a student. The probability is \(\dfrac{6}{15}\), when the first draw selects a staff member. The probability of drawing a student's name changes for each of the trials and, therefore, violates the condition of independence.
Exercise \(\PageIndex{9}\)
A lacrosse team is selecting a captain. The names of all the seniors are put into a hat, and the first three that are drawn will be the captains. The names are not replaced once they are drawn (one person cannot be two captains). You want to see if the captains all play the same position. State whether this is binomial or not and state why.
Answer
This is not binomial because the names are not replaced, which means the probability changes for each time a name is drawn. This violates the condition of independence.
References
- “Access to electricity (% of population),” The World Bank, 2013. Available online at http://data.worldbank.org/indicator/...first&sort=asc (accessed May 15, 2015).
- “Distance Education.” Wikipedia. Available online at http://en.Wikipedia.org/wiki/Distance_education (accessed May 15, 2013).
- “NBA Statistics – 2013,” ESPN NBA, 2013. Available online at http://espn.go.com/nba/statistics/_/seasontype/2 (accessed May 15, 2013).
- Newport, Frank. “Americans Still Enjoy Saving Rather than Spending: Few demographic differences seen in these views other than by income,” GALLUP® Economy, 2013. Available online at http://www.gallup.com/poll/162368/am...-spending.aspx (accessed May 15, 2013).
- Pryor, John H., Linda DeAngelo, Laura Palucki Blake, Sylvia Hurtado, Serge Tran. The American Freshman: National Norms Fall 2011. Los Angeles: Cooperative Institutional Research Program at the Higher Education Research Institute at UCLA, 2011. Also available online at http://heri.ucla.edu/PDFs/pubs/TFS/N...eshman2011.pdf (accessed May 15, 2013).
- “The World FactBook,” Central Intelligence Agency. Available online at https://www.cia.gov/library/publicat...k/geos/af.html (accessed May 15, 2013).
- “What are the key statistics about pancreatic cancer?” American Cancer Society, 2013. Available online at http://www.cancer.org/cancer/pancrea...key-statistics (accessed May 15, 2013).
Chapter Review
A statistical experiment can be classified as a binomial experiment if the following conditions are met:
There are a fixed number of trials, \(n\).
There are only two possible outcomes, called "success" and, "failure" for each trial. The letter \(p\) denotes the probability of a success on one trial and \(q\) denotes the probability of a failure on one trial.
The \(n\) trials are independent and are repeated using identical conditions.
The outcomes of a binomial experiment fit a binomial probability distribution. The random variable \(X =\) the number of successes obtained in the \(n\) independent trials. The mean of \(X\) can be calculated using the formula \(\mu = np\), and the standard deviation is given by the formula \(\sigma = \sqrt{npq}\).
Formula Review
- \(X \sim B(n, p)\) means that the discrete random variable \(X\) has a binomial probability distribution with \(n\) trials and probability of success \(p\).
- \(X =\) the number of successes in \(n\) independent trials
- \(n =\) the number of independent trials
- \(X\) takes on the values \(x = 0, 1, 2, 3, \dotsc, n\)
- \(p =\) the probability of a success for any trial
- \(q =\) the probability of a failure for any trial
- \(p + q = 1\)
- \(q = 1 – p\)
The mean of \(X\) is \(\mu = np\). The standard deviation of \(X\) is \(\sigma = \sqrt{npq}\).
Contributors and Attributions
Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/30189442-699...b91b9de@18.114.
Use the following information to answer the next eight exercises: The Higher Education Research Institute at UCLA collected data from 203,967 incoming first-time, full-time freshmen from 270 four-year colleges and universities in the U.S. 71.3% of those students replied that, yes, they believe that same-sex couples should have the right to legal marital status. Suppose that you randomly pick eight first-time, full-time freshmen from the survey. You are interested in the number that believes that same sex-couples should have the right to legal marital status.
Exercise 4.4.9
In words, define the random variable \(X\).
Answer
\(X =\) the number that reply “yes”
Exercise 4.4.10
\(X \sim\) _____(_____,_____)
Exercise 4.4.11
What values does the random variable \(X\) take on?
Answer
0, 1, 2, 3, 4, 5, 6, 7, 8
Exercise 4.4.12
Construct the probability distribution function (PDF).
| \(x\) | \(P(x)\) |
|---|---|
Exercise 4.4.13
On average (\(\mu\)), how many would you expect to answer yes?
Answer
5.7
Exercise 4.4.14
What is the standard deviation (\(\sigma\))?
Exercise 4.4.15
What is the probability that at most five of the freshmen reply “yes”?
Answer
0.4151
Exercise 4.4.16
What is the probability that at least two of the freshmen reply “yes”?
Glossary
- Binomial Experiment
- a statistical experiment that satisfies the following three conditions:
-
- There are a fixed number of trials, \(n\).
- There are only two possible outcomes, called "success" and, "failure," for each trial. The letter \(p\) denotes the probability of a success on one trial, and \(q\) denotes the probability of a failure on one trial.
- The \(n\) trials are independent and are repeated using identical conditions.
- Bernoulli Trials
- an experiment with the following characteristics:
-
- There are only two possible outcomes called “success” and “failure” for each trial.
- The probability \(p\) of a success is the same for any trial (so the probability \(q = 1 − p\) of a failure is the same for any trial).
- Binomial Probability Distribution
- a discrete random variable (RV) that arises from Bernoulli trials; there are a fixed number, \(n\), of independent trials. “Independent” means that the result of any trial (for example, trial one) does not affect the results of the following trials, and all trials are conducted under the same conditions. Under these circumstances the binomial RV \(X\) is defined as the number of successes in \(n\) trials. The notation is: \(X ~ B(n, p)\). The mean is \(\mu = np\) and the standard deviation is \(\sigma = \sqrt{npq}\). The probability of exactly \(x\) successes in \(n\) trials is
\(P(X = x) = {n \choose x}p^{x}q^{n-x}\).


