5.7: Arguments with Euler Diagrams
- Page ID
- 30277
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Determine the validity of an argument using an Euler diagram
We can interpret a deductive argument visually with an Euler diagram, which is essentially the same thing as a Venn diagram, where we use circles to represent statements. This can make it easier to determine whether the argument is valid or invalid.
To analyze an argument with an Euler diagram:
- Draw an Euler diagram based on the premises of the argument.
- The argument is invalid if there is a way to draw the diagram that makes the conclusion false.
- The argument is valid if the diagram cannot be drawn to make the conclusion false.
- If the premises are insufficient to determine the location of an element or a set mentioned in the conclusion, then the argument is invalid.
Remember, it only takes one counter-example to show the conclusion is false and make the argument invalid.
Universal Affirmative: All A are B.
Universal Negative: No A are B.
Particular Affirmative: Some A are B. Note that the "x" signifies the region where at least one A is B.
Particular Negative: Some A are not B. The "x" signifies the region where at least one A is not B.
Specific Affirmative: x is A.
Specific Negative: x is not A.
Consider the deductive argument “All cats are mammals and a tiger is a cat, so a tiger is a mammal.” Use an Euler diagram to determine if this argument is valid.
Solution
The premises are:
All cats are mammals.
A tiger is a cat.
The conclusion is:
A tiger is a mammal.
Both the premises are true. From the first premise, we draw the set of cats as a subset of the set of mammals. From the second premise, we are told that a tiger is contained within the set of cats. From that, we can see in the Euler diagram that the tiger must also be inside the set of mammals, so the conclusion is valid.
Determine the validity of this argument:
\(\begin{array} {ll} \text{Premise:} & \text{All cats are scared of vacuum cleaners.} \\ \text{Premise:} & \text{Max is a cat.} \\ \text{Conclusion:} & \text{Max is scared of vacuum cleaners.} \end{array}\)
- Answer
-
Valid. Cats are a subset of creatures that are scared by vacuum cleaners. Max is in the set of cats, so he must also be in the set of creatures that are scared by vacuum cleaners.
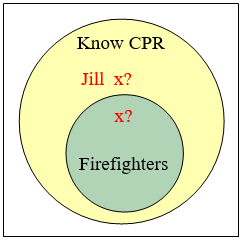
Determine the validity of this argument:
\(\begin{array} {ll} \text{Premise:} & \text{All firefighters know CPR.} \\ \text{Premise:} & \text{Jill knows CPR.} \\ \text{Conclusion:} & \text{Jill is a firefighter.} \end{array}\)
Solution
From the first premise, we know that firefighters all lie inside the set of those who know CPR. (Firefighters are a subset of people who know CPR.) From the second premise, we know that Jill is a member of that larger set, but we do not have enough information to know whether she also is a member of the smaller subset that is firefighters.
Since the conclusion does not necessarily follow from the premises, this is an invalid argument. It’s possible that Jill is a firefighter, but the structure of the argument doesn’t allow us to conclude that she definitely is.
It is important to note that whether or not Jill is actually a firefighter is not important in evaluating the validity of the argument; we are concerned with whether the premises are enough to prove the conclusion.
Determine the validity of this argument:
\(\begin{array} {ll} \text{Premise:} & \text{All bicycles have two wheels.} \\ \text{Premise:} & \text{This Harley-Davidson has two wheels.} \\ \text{Conclusion:} & \text{This Harley-Davidson is a bicycle.} \end{array}\)
- Answer
-
Invalid. The set of bicycles is a subset of the set of vehicles with two wheels; the Harley-Davidson is in the set of two-wheeled vehicles but not necessarily in the smaller circle.
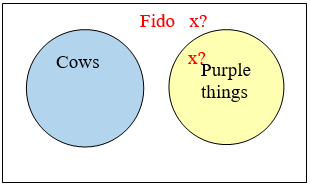
Determine the validity of this argument:
\(\begin{array} {ll} \text{Premise:} & \text{No cows are purple.} \\ \text{Premise:} & \text{Fido is not a cow.} \\ \text{Conclusion:} & \text{Fido is purple.} \end{array}\)
- Answer
-
Invalid. Since no cows are purple, we know there is no overlap between the set of cows and the set of purple things. We know Fido is not in the cow set, but that is not enough to conclude that Fido is in the purple things set.
In addition to these categorical style premises of the form “all ___”, “some ____”, and “no ____”, it is also common to see premises that are conditionals.
\(\begin{array} {ll} \text{Premise:} & \text{If you live in Seattle, you live in Washington.} \\ \text{Premise:} & \text{Marcus does not live in Seattle.} \\ \text{Conclusion:} & \text{Marcus does not live in Washington.} \end{array}\)
Solution
From the first premise, we know that the set of people who live in Seattle is inside the set of those who live in Washington. From the second premise, we know that Marcus does not lie in the Seattle set, but we have insufficient information to know whether Marcus lives in Washington or not. This is an invalid argument.
Determine the validity of this argument:
\(\begin{array} {ll} \text{Premise:} & \text{If you have lipstick on your collar, then you are cheating on me.} \\ \text{Premise:} & \text{If you are cheating on me, then I will divorce you.} \\ \text{Premise:} & \text{ You do not have lipstick on your collar.} \\ \text{Conclusion:} & \text{I will not divorce you.} \end{array}\)
- Answer
-
Invalid. Lipstick on your collar is a subset of scenarios in which you are cheating, and cheating is a subset of the scenarios in which I will divorce you. Although it is wonderful that you don’t have lipstick on your collar, you could still be cheating on me, and I will divorce you. In fact, even if you aren’t cheating on me, I might divorce you for another reason. You’d better shape up.
