5.4: Equivalent Statements and Variations of the Conditional
- Page ID
- 41384
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
- Determine if 2 statements are logically equivalent
- Apply De Morgan's Laws
- Determine the converse, inverse and contrapositive of a conditional statement
- Determine the negation of a conditional statement
It is often of interest to determine if logic statements have the same truth values. For example, "It is not raining or there are clouds in the sky" has the same truth values as "If it is raining, then there are clouds in the sky." See the example below to verify the values in their truth tables are the same.
Two statements are logically equivalent if they have the same simple statements and when their truth tables are computed, the final columns in the tables are identical. The symbol for equivalent statements is \(\equiv\).
Show that "It is not raining or there are clouds in the sky" is equivalent to "If it is raining, then there are clouds in the sky."
Solution
Let \(p\) be the statement "it is raining" and \(q\) be the statement "there are clouds in the sky." "It is not raining or there are clouds in the sky" is written symbolically as \(\sim p \vee q \) and "If it is raining, then there are clouds in the sky" is written symbolically as \(p \rightarrow q\). The truth tables are as follows:
\(\begin{array}{|c|c|c|c|}
\hline p & q & \sim p & \sim p \vee q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F}\\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T}\\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T}\\
\hline
\end{array}\)
\(\begin{array}{|c|c|c|}
\hline p & q & p \rightarrow q \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)
Since the final answer columns of the truth tables are the same, the statements are equivalent. \( \sim p \vee q \equiv p \rightarrow q\)
Augustus De Morgan formalized two rules of logic that had previously been known informally. They allow us to rewrite the negation of a conjunction as a disjunction, and vice-versa.
For example, suppose you want to schedule a meeting with two colleagues at 4:30 PM on Friday, and you need both of them to be available at that time. What situation would make it impossible to have the meeting? It is NOT the case that colleague \(A\) is available AND colleague \(B\) is available: \(\sim (A \wedge B) \). This situation is equivalent to either colleague \(A\) NOT being available OR colleague \(B\) NOT being available: \( \sim A \ \vee \sim B \).
The negation of a conjunction is logically equivalent to the disjunction of the negation of the statements making up the conjunction. To negate an “and” statement, negate each part and change the “and” to “or”.
\(\sim(p \wedge q) \ \equiv \ \sim p \ \vee \sim q\)
The negation of a disjunction is logically equivalent to the conjunction of the negation of the statements making up the disjunction. To negate an “or” statement, negate each part and change the “or” to “and”.
\(\sim(p \vee q) \ \equiv\ \sim p \ \wedge \sim q\)
For Valentine’s Day, you did not get your sweetie flowers or candy. Which of the following statements is logically equivalent?
- You did not get them flowers or did not get them candy.
- You did not get them flowers and did not get them candy.
- You got them flowers or got them candy.
Solution
Let \(f\) be the statement "You got your sweetie flowers" and let \(c\) be the statement "You got your sweetie candy." The compound statement "You did not get your sweetie flowers or candy" can be written symbolically as \(\sim(f \vee c)\). By De Morgan's Laws,
\(\sim(f \vee c) \ \equiv \ \sim f \ \wedge \sim c\)
This is answer b, you did not get your sweetie flowers and you did not get your sweetie candy.
To serve as the President of the US, a person must have been born in the US, must be at least 35 years old, and must have lived in the US for at least 14 years. What minimum set of conditions would disqualify someone from serving as President?
- Answer
-
Failing to meet just one of the three conditions is all it takes to be disqualified since the compound statement is made up of conjunctions. A person is disqualified if they were not born in the US, or are not at least 35 years old, or have not lived in the US for at least 14 years. The key word here is “or” instead of “and”.
For any conditional, there are three related statements, the converse, the inverse, and the contrapositive.
The original conditional is \(\quad\) "if \(p,\) then \(q\)" \(\quad p \rightarrow q\)
The converse is \(\quad\) "if \(q,\) then \(p\)" \(\quad q \rightarrow p\)
The inverse is \(\quad\) "if not \(p,\) then not \(q\)" \(\quad \sim p \rightarrow \sim q\)
The contrapositive is \(\quad\) "if not \(q,\) then not \(p\)" \(\quad \sim q \rightarrow \sim p\)
Consider again the conditional “If it is raining, then there are clouds in the sky.” It seems reasonable to assume that this is true.
The converse would be “If there are clouds in the sky, then it is raining.” This is not always true.
The inverse would be “If it is not raining, then there are not clouds in the sky.” Likewise, this is not always true.
The contrapositive would be “If there are not clouds in the sky, then it is not raining.” This statement is true, and is equivalent to the original conditional.
Looking at truth tables, we can see that the original conditional and the contrapositive are logically equivalent, and that the converse and inverse are logically equivalent.
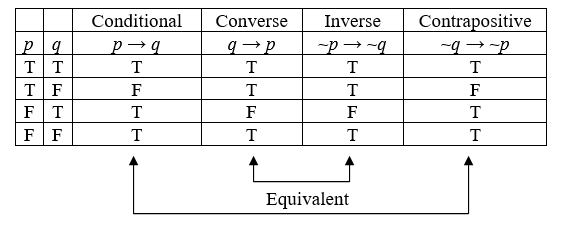
A conditional statement and its contrapositive are logically equivalent: \(p \rightarrow q \ \equiv \ \sim q \rightarrow \sim p\).
The converse and inverse of a conditional statement are logically equivalent: \(q \rightarrow p \ \equiv \ \sim p \rightarrow \sim q\).
A conditional statement is logically equivalent to the disjunction of the negation of its antecedent and its consequent: \(p \rightarrow q \ \equiv \ \sim p \ \vee q\).
The negation of a conditional statement is logically equivalent to a conjunction of the antecedent and the negation of the consequent.
\(\sim(p \rightarrow q) \ \equiv \ p \ \wedge \sim q\)
Write the negation of the statement "If you study, then you will pass this class."
Solution
Let \(p\) be "you study," and \(q\) be "you will pass this class." The symbolic form of the statement is \(p \rightarrow q\). The negation is \(p \ \wedge \sim q\). Translating back to English, the negated statement is "You study and you will not pass this class." Note that this statement is only true when you do study but do not pass the class.


