2.8: Solids
- Page ID
- 30341
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify geometric solids.
- Find the volume of geometric solids.
- Find the volume of a composite geometric solid.
Introduction
Living in a two-dimensional world would be pretty boring. Thankfully, all of the physical objects that you see and use every day, such as computers, phones, cars, and shoes, exist in three dimensions. They all have length, width, and height. (Even very thin objects like a piece of paper are three-dimensional. The thickness of a piece of paper may be a fraction of a millimeter, but it does exist.)
In the world of geometry, it is common to see three-dimensional figures. In mathematics, a flat side of a three-dimensional figure is called a face. Polyhedrons are shapes that have four or more faces, each one being a polygon. These include cubes, prisms, and pyramids. Sometimes you may even see single figures that are composites of two of these figures. Let’s take a look at some common polyhedrons.
Identifying Solids
The first set of solids contains rectangular bases. Have a look at the table below, which shows each figure in both solid and transparent form.
| Name | Definition | Solid Form | Transparent Form |
| Cube | A six-sided polyhedron that has congruent squares as faces. |  |
 |
| Rectangular prism | A polyhedron that has three pairs of congruent, rectangular, parallel faces. |  |
 |
| Pyramid | A polyhedron with a polygonal base and a collection of triangular faces that meet at a point. |  |
 |
Notice the different names that are used for these figures. A cube is different than a square, although they are sometimes confused with each other; a cube has three dimensions, while a square only has two. Likewise, you would describe a shoebox as a rectangular prism (not simply a rectangle), and the ancient pyramids of Egypt as…well, as pyramids (not triangles)! A rectangular prism is casually referred to as a box.
In this next set of solids, each figure has a circular base.
| Name | Definition | Solid Form | Transparent Form |
| Cylinder | A solid figure with a pair of circular, parallel bases and a round, smooth face between them. |  |
 |
| Cone | A solid figure with a single circular base and a round, smooth face that diminishes to a single point. |  |
 |
Take a moment to compare a pyramid and a cone. Notice that a pyramid has a rectangular base and flat, triangular faces; a cone has a circular base and a smooth, rounded body.
Finally, let’s look at a shape that is unique: a sphere.
| Name | Definition | Solid Form | Transparent Form |
| Sphere | A solid, round figure where every point on the surface is the same distance from the center. |  |
 |
There are many spherical objects all around you: soccer balls, tennis balls, and baseballs being three common items. While they may not be perfectly spherical, they are generally referred to as spheres.
A three-dimensional figure has the following properties:
- It has a rectangular base.
- It has four triangular faces.
What kind of a solid is it?
Solution
 |
A rectangular base indicates that it must be a cube, rectangular prism, or pyramid. |
 |
Since the faces are triangular, it must be a pyramid. |
Thus, the solid is a pyramid.
Volume
Recall that perimeter measures one dimension (length), and area measures two dimensions (length and width). To measure the amount of space a three-dimensional figure takes up, you use another measurement called volume.
To visualize what “volume” measures, look back at the transparent image of the rectangular prism mentioned earlier (or just think of an empty shoebox). Imagine stacking identical cubes inside that box so that there are no gaps between any of the cubes. Imagine filling up the entire box in this manner. If you counted the number of cubes that fit inside that rectangular prism, you would have its volume.

Volume is measured in cubic units. The shoebox illustrated above may be measured in cubic inches (usually represented as in3 or inches3), while the Great Pyramid of Egypt would be more appropriately measured in cubic meters (m3 or meters3).
To find the volume of a geometric solid, you could create a transparent version of the solid, create a bunch of 1 by 1 by 1 cubes, and then stack them carefully inside. However, that would take a long time! A much easier way to find the volume is to become familiar with some geometric formulas, and to use those instead.
Let’s go through the geometric solids once more and list the volume formula for each.
As you look through the list below, you may notice that some of the volume formulas look similar to their area formulas. To find the volume of a rectangular prism, you find the area of the base and then multiply that by the height.
| Name | Transparent Form | Volume Formula |
| Cube | 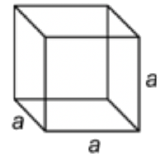 |
\(\ V=a \cdot a \cdot a=a^{3}\) \(\ a=\text { the length of one side }\) |
| Rectangular prism |  |
\(\ V=l \cdot w \cdot h\) \(\ \begin{array}{l} |
| Pyramid |  |
\(\ V=\dfrac{l \cdot w \cdot h}{3}\) \(\ \begin{array}{l} |
Remember that all cubes are rectangular prisms, so the formula for finding the volume of a cube is the area of the base of the cube times the height.
Now let’s look at solids that have a circular base.
| Name | Transparent Form | Volume Formula |
| Cylinder |  |
\(\ V=\pi \cdot r^{2} \cdot h\) \(\ \begin{array}{l} |
| Cone |  |
\(\ V=\dfrac{\pi \cdot r^{2} \cdot h}{3}\) \(\ \begin{array}{l} |
Here you see the number \(\ \pi\) again.
The volume of a cylinder is the area of its base, \(\ \pi r^{2}\), times its height, \(\ h\).
Compare the formula for the volume of a cone (\(\ V=\dfrac{\pi \cdot r^{2} \cdot h}{3}\)) with the formula for the volume of a pyramid (\(\ V=\dfrac{l \cdot w \cdot h}{3}\)). The numerator of the cone formula is the volume formula for a cylinder, and the numerator of the pyramid formula is the volume formula for a rectangular prism. Then divide each by 3 to find the volume of the cone and the pyramid. Looking for patterns and similarities in the formulas can help you remember which formula refers to a given solid.
Finally, the formula for a sphere is provided below. Notice that the radius is cubed, not squared and that the quantity \(\ \pi r^{3}\) is multiplied by \(\ \dfrac{4}{3}\).
| Name | Transparent Form | Volume Formula |
| Sphere |  |
\(\ V=\dfrac{4}{3} \pi r^{3}\) \(\ r=\text { radius }\) |
Applying the Formulas
You know how to identify the solids, and you also know the volume formulas for these solids. To calculate the actual volume of a given shape, all you need to do is substitute the solid’s dimensions into the formula and calculate.
In the examples below, notice that cubic units (meters3, inches3, feet3) are used.
Find the volume of a cube with side lengths of 6 meters.
Solution
| \(\ \begin{array}{l} V&=a \cdot a \cdot a=a^{3}\\ a&=\text { side length } \end{array}\) |
Identify the proper formula to use. |
| \(\ V=6 \cdot 6 \cdot 6=6^{3}\) | Substitute \(\ a=6\) into the formula. |
| \(\ V=6 \cdot 6 \cdot 6=216\) | Calculate the volume. |
Thus, the volume of the cube is \(\ 216 \text { meters}^{3}\).
Find the volume of the solid figure shown below.

Solution
| Pyramid | Identify the shape. It has a rectangular base and rises to a point, so it is a pyramid. |
| \(\ V=\dfrac{l \cdot w \cdot h}{3}\) | Identify the proper formula to use. |
| \(\ \begin{array}{l} l&=\text { length } \\ w&=\text { width } \\ h&=\text { height } \\ \\ 4&=\text { length } \\ 3&=\text { width } \\ 8&=\text { height } \end{array}\) |
Use the image to identify the dimensions. Then substitute \(\ l=4, w=3, \text{and }h=8\) into the formula. |
| \(\ \begin{array}{c} V=\dfrac{4 \cdot 3 \cdot 8}{3} \\ V=\dfrac{96}{3} \\ V=32 \end{array}\) |
Calculate the volume and choose the appropriate units. |
The volume of the pyramid is \(\ 32 \text { inches}^{3}\).
Find the volume of the solid shown below.
Use 3.14 for \(\pi\), and round the answer to the nearest hundredth.

Solution
| Cylinder | Identify the shape. It has a circular base and has uniform thickness (or height), so it is a cylinder. |
| \(\ V=\pi \cdot r^{2} \cdot h\) | Identify the proper formula to use. |
| \(\ V=\pi \cdot 7^{2} \cdot 1\) | Use the image to identify the dimensions. Then substitute \(\ r=7\) and \(\ h=1\) into the formula. |
| \(\ \begin{array}{r} V=\pi \cdot 49 \cdot 1 \\ V=49 \pi \\ V \approx 153.86 \end{array}\) |
Calculate the volume, using 3.14 as an approximation for \(\pi\). |
The volume of the cylinder is 49\(\pi\) or approximately \(\ 153.86 \text { feet}^{3}\).
Find the volume of a rectangular prism that is 8 inches long, 3 inches wide, and 10 inches tall.
- Answer
-
To find the volume of the rectangular prism, use the formula \(\ V=l \cdot w \cdot h\), and then substitute in the values for the length, width, and height. \(\ V = 8 \text{ inches }\cdot 3\text{ inches }\cdot 10\text{ inches }=240 \text{ inches}^3\).
Composite Solids
Composite geometric solids are made from two or more geometric solids. You can find the volume of these solids as well, as long as you are able to figure out the individual solids that make up the composite shape.
Look at the image of a capsule below. Each end is a half-sphere. You can find the volume of the solid by taking it apart. What solids can you break this shape into?

You can break it into a cylinder and two half-spheres.

Two half-spheres form a whole one, so if you know the volume formulas for a cylinder and a sphere, you can find the volume of this capsule.
If the radius of the spherical ends is 6 inches, find the volume of the solid below. Use 3.14 for \(\pi\). Round your final answer to the nearest whole number.

Solution
 |
Identify the composite solids. This capsule can be thought of as a cylinder with a half-sphere on each end. |
| Volume of a cylinder: \(\ \pi \cdot r^{2} \cdot h\) Volume of a sphere: \(\ \dfrac{4}{3} \pi r^{3}\) |
Identify the proper formulas to use. |
| Volume of a cylinder: \(\ \pi \cdot 6^{2} \cdot 24\) Volume of a sphere: \(\ \dfrac{4}{3} \pi \cdot 6^{3}\) |
Substitute the dimensions into the formulas. The height of a cylinder refers to the section between the two circular bases. This dimension is given as 24 inches, so \(\ h=24\). |
| Volume of the cylinder: \(\ \begin{aligned} V &=\pi \cdot 36 \cdot 24 \\ &=864 \cdot \pi \\ & \approx 2712.96 \end{aligned}\) Volume of the sphere: \(\ \begin{aligned} V &=\dfrac{4}{3} \pi \cdot 216 \\ &=288 \cdot \pi \\ & \approx 904.32 \end{aligned}\) |
The radius of the sphere is 6 inches. You can use \(\ r=6\) in both formulas. Calculate the volume of the cylinder and the sphere. |
| Volume of capsule: \(\ 2712.96+904.32 \approx 3617.28\) |
Add the volumes. |
The volume of the capsule is \(\ 1152 \pi\) or approximately \(\ 3617 \text { inches}^{3}\).
A sculptor carves a rectangular prism out of a solid piece of wood. Then, at the top, she hollows out an inverted pyramid. The solid, and its dimensions, are shown at right. What is the volume of the finished piece?

Solution
| Identify the composite solids. This sculpture can be thought of as a rectangular prism with a pyramid removed. Hence the volume of the pyramid will be subtracted (taken away) from the volume of the box. | |
| Volume of rectangular prism: \(\ l \cdot w \cdot h\) Volume of pyramid: \(\ \dfrac{l \cdot w \cdot h}{3}\) |
Identify the proper formulas to use. |
| Volume of rectangular prism: \(\ 1 \cdot 1 \cdot 8=8\) Volume of pyramid: \(\ \dfrac{1 \cdot 1 \cdot 2}{3}=\dfrac{2}{3}\) |
Substitute the dimensions into the formulas, and calculate. |
| Volume of sculpture: \(\ V=8-\dfrac{2}{3}=7\dfrac{1}{3}\) | Subtract the volume of the pyramid from the volume of the rectangular prism. |
The volume of the sculpture is \(\ 7 \dfrac{1}{3} \text { feet}^{3}\).
A machine takes a solid cylinder with a height of 9 mm and a diameter of 7 mm, and bores a hole all the way through it. The hole that it creates has a diameter of 3 mm. Which of the following expressions would correctly find the volume of the solid?

- \(\ \left(\pi \cdot 7^{2} \cdot 9\right)-\left(\pi \cdot 3^{2} \cdot 9\right)\)
- \(\ \left(\pi \cdot 3.5^{2} \cdot 9\right)-\left(\pi \cdot 1.5^{2} \cdot 9\right)\)
- \(\ \left(\pi \cdot 7^{2} \cdot 9\right)+\left(\pi \cdot 3^{2} \cdot 9\right)\)
- \(\ \left(\pi \cdot 3.5^{2} \cdot 9\right)+\left(\pi \cdot 1.5^{2} \cdot 9\right)\)
- Answer
-
B. You find the volume of the entire cylinder by multiplying \(\ \pi \cdot 3.5^{2} \cdot 9\), then subtract the empty cylinder in the middle, which is found by multiplying \(\ \pi \cdot 1.5^{2} \cdot 9\).
Summary
Three-dimensional solids have length, width, and height. You use a measurement called volume to figure out the amount of space that these solids take up. To find the volume of a specific geometric solid, you can use a volume formula that is specific to that solid. Sometimes, you will encounter composite geometric solids. These are solids that combine two or more basic solids. To find the volume of these, identify the simpler solids that make up the composite figure, find the volumes of those solids, and combine them as needed.


