8.3: A Confidence Interval for a Population Standard Deviation Unknown
- Page ID
- 14687
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In practice, we rarely know the population standard deviation. The point estimate for the standard deviation, \(s\), is substituted in the formula for the confidence interval for the population standard deviation. However, instead of using the standard normal Z score, we will use a t distribution.
William S. Gosset (1876–1937) of the Guinness brewery in Dublin, Ireland, ran into this problem. His experiments with hops and barley produced very few samples. Just replacing \(\sigma\) with \(s\) did not produce accurate results when he tried to calculate a confidence interval. He realized that he could not use a normal distribution for the calculation; he found that the actual distribution depends on the sample size. This problem led him to "discover" what is called the Student's t-distribution. The name comes from the fact that Gosset wrote under the pen name "A Student."
Up until the mid-1970s, some statisticians used the normal distribution approximation for large sample sizes and used the Student's t-distribution only for sample sizes of at most 30 observations. However, now when we do not know the population standard deviation, we will use the t-distribution. As the sample size, \n\ increases the t distribution approaches the standard normal distribution.
If you draw a simple random sample of size \(n\) from a population with mean \(\mu\) and unknown population standard deviation \(\sigma\) and calculate the t-score
\[t=\frac{\overline{x}-\mu}{\left(\frac{s}{\sqrt{n}}\right)}\]
then the t-scores follow a Student's t-distribution with \(\bf{n – 1}\) degrees of freedom. The t-score has the same interpretation as the z-score. It measures how far in standard deviation units \(\overline x\) is from its mean \mu. For each sample size \(n\), there is a different Student's t-distribution.
The degrees of freedom, \(\bf{n – 1}\), come from the calculation of the sample standard deviation \(\bf{s}\). Remember when we first calculated a sample standard deviation, we divided the squared deviations by \(n – 1\). Still, we used \(n\) deviations (\(\overline x\) values) to calculate \(\bf{s}\). Because the sum of the deviations is zero, we can find the last deviation once we know the other \(\bf{n – 1}\) deviations. The other \(\bf{n – 1}\) deviations can change or vary freely. We call the number \(\bf{n – 1}\) the degrees of freedom (\(df\)) in recognition that one is lost in the calculations. The effect of losing a degree of freedom is that the t-value increases and the confidence interval increases in width.
Properties of the Student's t-Distribution
- The graph for the Student's t-distribution is similar to the standard normal curve, a t distribution with infinite degrees of freedom is the normal distribution. You can confirm this by reading the bottom line at infinite degrees of freedom for a familiar level of confidence, e.g., at column 0.05, 95% level of confidence, we find the t-value of 1.96 at infinite degrees of freedom.
- The mean for the Student's t-distribution is zero, and the distribution is symmetric about zero, again like the standard normal distribution.
- The Student's t-distribution has more probability in its tails than the standard normal distribution because the spread of the t-distribution is greater than the spread of the standard normal. So the graph of the Student's t-distribution will be thicker in the tails and shorter in the center than the standard normal distribution graph.
- The exact shape of the Student's t-distribution depends on the degrees of freedom. As the degrees of freedom increases, the graph of Student's t-distribution becomes more like the graph of the standard normal distribution.
- The underlying population of individual observations is assumed to be normally distributed with an unknown population mean \(\mu\) and unknown population standard deviation \(\sigma\). This assumption comes from the Central Limit theorem because the individual observations, in this case, are the \(\overline x\)s of the sampling distribution. If it is normal, then the assumption is met and doesn't need discussion.
A probability table for the Student's t-distribution is used to calculate t-values at various commonly-used levels of confidence. The table gives t-scores that correspond to the confidence level (column) and freedom degrees (row). When using a t-table, note that some tables are formatted to show the confidence level in the column headings, while the column headings in some tables may show only corresponding areas in one or both tails. Notice that at the bottom the table will show the t-value for infinite degrees of freedom. Mathematically, as the degrees of freedom increase, the \(t\) distribution approaches the standard normal distribution. You can find familiar Z-values by looking in the relevant alpha column and reading the t-value in the last row.
You can also find the t-value by using the following formula in an Excel spreadsheet.
=T.INV.2T(1- \alpha\, n-1)
A Student's t table (Table \(\PageIndex{6}\)) gives t-scores given the degrees of freedom and the right-tailed probability.
The Student's t distribution has one of the most desirable properties of the normal: it is symmetrical. What the Student's t distribution does is spread out the horizontal axis so it takes a larger number of standard deviations to capture the same amount of probability. In reality, there are an infinite number of Student's t distributions, one for each adjustment to the sample size. As the sample size increases, the Student's t distribution become more and more like the normal distribution. This relationship between the Student's t distribution and the normal distribution is shown in Figure \(\PageIndex{8}\).
This is another example of one distribution limiting another one, in this case, the normal distribution is the limiting distribution of the Student's t when the degrees of freedom in the Student's t approaches infinity. This conclusion comes directly from the derivation of the Student's t distribution by Mr. Gosset. He recognized the problem as having few observations and no estimate of the population standard deviation. He was substituting the sample standard deviation and getting volatile results. He, therefore, created the Student's t distribution as a ratio of the normal distribution and Chi-squared distribution. The Chi-squared distribution is itself a ratio of two variances, in this case, the sample variance and the unknown population variance. Thus, the Student's t distribution is tied to the normal distribution but has degrees of freedom that come from those of the Chi-squared distribution. The algebraic solution demonstrates this result.
Development of Student's t-distribution:
- \(t=\frac{z}{\sqrt{\frac{\chi^{2}}{v}}}\)
Where \(Z\) is the standard normal distribution and \(X^2\) is the chi-squared distribution with \(v\) degrees of freedom.
- \(t=\frac{\frac{(\overline x-\mu)}{\sigma}}{\sqrt{\frac{\frac{s^{2}}{(n-1)}}{\frac{\sigma^{2}}{(n-1)}}}}\)
by substitution, and thus Student's t with \(v = n − 1\) degrees of freedom is:
- \(t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\)
Restating the formula for a confidence interval for the mean for cases when we do not know the population standard deviation, \(\sigma\):
\[\overline{x}-t_{\nu, \alpha}\left(\frac{s}{\sqrt{n}}\right) \leq \mu \leq \overline{x}+t_{\nu, \alpha}\left(\frac{s}{\sqrt{n}}\right)\nonumber\]
Here the point estimate of the population standard deviation, \(s\) has been substituted for the population standard deviation, \(\sigma\), and \(t_{\nu}\),\(\alpha\) has been substituted for \(Z_{\alpha}\). The Greek letter \(\nu\) (pronounced nu) is placed in the general formula in recognition that there are many Student \(t_{\nu}\) distributions, one for each sample size. \(\nu\) is the symbol for the degrees of freedom of the distribution and depends on the size of the sample. Often df is used to abbreviate degrees of freedom. For this type of problem, the degrees of freedom is \(\nu = n-1\), where \(n\) is the sample size. To look up a probability in the Student's t table we have to know the degrees of freedom in the problem.
Example \(\PageIndex{4}\)
Spring break can be a very expensive holiday. A sample of 80 students is surveyed, and the average amount spent by students on travel and beverages is $593.84. The sample standard deviation is approximately $369.34.
Construct a 92% confidence interval for the population mean amount of money spent by spring breakers.
- Answer
-
Solution 8.4
We begin with the confidence interval for a mean. We use the formula for a mean because the random variable is dollars spent and this is a continuous random variable. The point estimate for the population standard deviation, s, has been substituted for the true population standard deviation. With 80 observations there is no concern for bias in the estimate of the confidence interval.
\[\mu=\overline{x} \pm\left[t_{(\mathrm{a} / 2)} \frac{s}{\sqrt{n}}\right]\nonumber\]
Substituting the values into the formula, we have:
\[\mu=593.84 \pm\left[1.77 \frac{369.34}{\sqrt{80}}\right]\nonumber\]
\(t_{(a / 2)}\) is found by using the Excel Spreadsheet. In a cell enter the following formula, = T.INV.2T(1-.92, 79) = 1.77 rounded to two decimal places. The solution for the interval is thus:
\[\mu=593.84 \pm 73.0894=(520.75,666.93)\nonumber\]
\[\$ 520.75 \leq \mu \leq \$ 666.93\nonumber\]
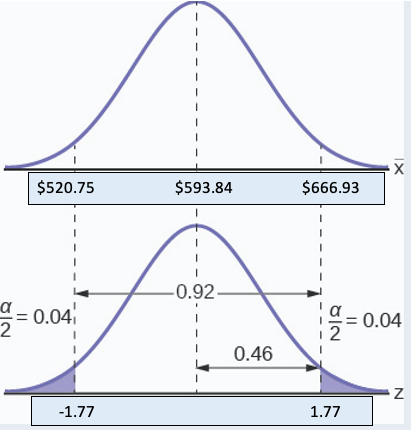
Figure \(\PageIndex{7}\)
Example \(\PageIndex{1}\)
The average earnings per share (EPS) for 10 industrial stocks randomly selected from those listed on the Dow-Jones Industrial Average was found to be \(\overline X = 1.85\) with a standard deviation of \(s=0.395\). Calculate a 99% confidence interval for the average EPS of all the industrials listed on the \(DJIA\).
\[\overline{x}-t_{v, \alpha}\left(\frac{s}{\sqrt{n}}\right) \leq \mu \leq \overline{x}+t_{\nu, \alpha}\left(\frac{s}{\sqrt{n}}\right)\nonumber\]
- Answer
-
To help visualize the process of calculating a confident interval we draw the appropriate distribution for the problem. In this case this is the Student’s t because we do not know the population standard deviation.
Figure \(\PageIndex{2}\) To find the appropriate t-value requires two pieces of information, the level of confidence desired and the degrees of freedom. The question asked for a 99% confidence level. On the graph this is shown where (\(1-\alpha\)), the level of confidence, is in the unshaded area. The tails, thus, have .005 probability each, \(\alpha/2\). The degrees of freedom for this type of problem is \(n - 1= 9\). From the Student’s t table, at the row marked 9 and column marked .005, is the number of standard deviations to capture 99% of the probability, 3.2498. These are then placed on the graph remembering that the Student’s \(t\) is symmetrical and so the t-value is both plus or minus on each side of the mean.
Using the Excel spreadsheet, the t-value to use in the confidence interval can be found by entering the following formula in a cell.
=T.INV.2T(1-.99, 9) = 3.2498
Inserting these values into the formula gives the result. These values can be placed on the graph to see the relationship between the distribution of the sample means, \(\overline X\)'s and the Student’s t distribution.
\[\mu=\overline{X} \pm t_{\alpha / 2, \mathrm{df}=n-1} \frac{s}{\sqrt{n}}=1.851 \pm 3.2498 \frac{0.395}{\sqrt{10}}=1.8551 \pm 0.406\nonumber\]
\[1.445 \leq \mu \leq 2.257\nonumber\]
We state the formal conclusion as :
With 99% confidence level, the average \(EPS\) of all the industries listed at \(DJIA\) is from $1.44 to $2.26.
Exercise \(\PageIndex{2}\)
You do a study of hypnotherapy to determine how effective it is in increasing the number of hours of sleep subjects get each night. You measure hours of sleep for 12 subjects with the following results. Construct a 95% confidence interval for the mean number of hours slept for the population (assumed normal) from which you took the data.
8.2; 9.1; 7.7; 8.6; 6.9; 11.2; 10.1; 9.9; 8.9; 9.2; 7.5; 10.5


