Ch 11.3 Test of Independence
( \newcommand{\kernel}{\mathrm{null}\,}\)
Contingency table
A contingency table is a table consisting of frequency counts of categorical data corresponding to two different variables. (One variable is used to categorize rows, the second is used to categorize columns.)
- It is used to calculate conditional probability.
- It is also used to study if row and column variables are independent or independent (associations.)
Test of independence
Approach: Compare expected counts with observed counts in a contingency table to determine association or dependency.
Example:
Given the survey summary of a group of students. Can we conclude choice of favorite snack is dependent on gender?
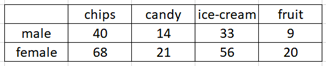
Use the total in each row and column to analysis the expected counts in each cell.
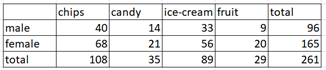
E=(row total)(column total)column total
Expected count tables.
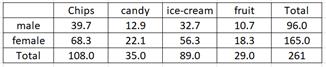
calculate χ2=∑(O−E)2E where O = observed counts, E = expected counts.
Large χ2 value implies big discrepancy from expected count so conclude row and columns are dependent. There is association between the variables.
Chi-square distribution is used with df = (r-1)(c-1) where r = number of rows, c = number columns.
Requirements:
-Expected counts in each cell is at least 5.
-Sample is simple random sample (SRS).
-The summaries are contingency table of counts.
Null hypothesis(H0) is always no association or independent.
Notes:
A small chi-square value means independence, because the observed counts agree with the expected counts.
The test of independence is always a right tail test.
because large χ2 value corresponds to Ha value.
Steps to conduct test of independence:
1) Write H0 and Ha and identify if claim is in H0 or Ha.
H0: the row and column variables are independent events. (no associations)
Ha: the row and column variables are dependent events. (has associations)
2) Input the contingency table in columns to Statdisk.
Analysis/Contingency table/Enter significance. Select the columns that contain the contingency table.
Evaluate. Output: degree of freedom , Test statistics χ2 and p-value.
3) If p-value ≤ α, Reject H0, conclude dependent. (the row and column variable are associated.)
If p-value > α, fail to reject H0, conclude independent.
4) Conclusion about the claim. If H0 is rejected, there is sufficient evidence, if H0 is failed to be rejected, there is not sufficient evidence.
5) Check that all expected count are at least 5. Use https://www.mathsisfun.com/data//chi-square-calculator.html
Ex1: Results of using nicotine patch and nicotine gum are summarized below. Test the claim results are independent of the method of treatment. Use α = 0.05
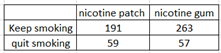
1) Write the null hypothesis:
H0: success and failure are independent of treatment.
Ha: success and failure are dependent of treatment.
Note: claim is H0.
2) Input the table to Statdisk. Analysis/Contingency Table/, input significance = 0.05, check column 1 , 2
Evaluate. Output: df = 1, Test stat χ2 = 2.9, p-value =0.0886.
3) Since 0.0886 > 0.05, fail to reject H0, conclude no association, the result and treatments are independent.
4) There is not sufficient evidence to reject the claim that success and failure are independent of the method of treatment. Conclude they are independent.
5) Check expected count from Mathisfun chi-square calculator.

all expected counts are at least 5, conclude requirement for Chi-square test of independence are satisified.
Ex2.
Echinacea experiment was by randomly assign patients to three treatment groups, a placebo group, a 20%-extract group and a 60%-extract group. Counts of infected and not infected for each group is summarized below. Test the claim that infected outcomes are dependent on type of treatments? Use α = 0.05.

1) H0: infected outcome is independent of treatment.
Ha: infected outcome is dependent of treatment.
Note: Claim is Ha.
Input data to statdisk, use Analysis/Contingency Table/, input significance = 0.05, Select column 1, 2, 3, evaluate.
Output: df = 2, test statistics = χ2 = 23.19., p-value = 0.
3) Since p-value < 0.05, Reject H0,
4) There is sufficient evidence to support the claim that infected rate is dependent of the type of treatment.
5) Use mathisfun chi-square calculator to find expected counts.

Requirement for Chi-square test is satisfied.
Test of homogeneity:
When sample data are summarized in a contingency table from different populations, and we can use chi-square test to determine whether those populations have the same proportion of some characteristic being considered, the hypothesis test is known as
“test of homogeneity”. The method is the same as that of “test of independence.”
A chi-square test of homogeneity is a test of the claim that different populations have the same proportions of some characteristics.
Example:
Sample are collected from three populations of workers. Use test of homogeneity to test the claim that choice of transportation are different among the three profession of workers.
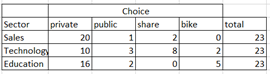
A test of homogeneity should be used instead of test of independence
The only difference is how samples are collected, the name of the test and how H0 and Ha are written. Everything else are the same as Test of independence.
Ex1. Test the claim that choices of transportation are different among the three profession of workers. Use a significant level of 0.05.
1) H0: proportion of the transportation choices are the same among the three professions.
Ha: At least one of the choices are different.
2) Input data to statdisk (do not enter the total columns). Analysis/Contingency Table/ Select column 1, 2, 3, 4, evaluate.
Output: df = 6 test stat = χ2=20.13 ., p-value = 0.0026
3) Since p-value < 0.05, Reject H0, conclude different proportions of choices between 3 populations.
4) There is sufficient evidence to support the claim that choices of transportation is different among the three populations of profession.
5) Calculate the expected counts by Mathisfun Chi-square calculator.

a few expected counts are below 5, so requirement for chi-square test is not satisfied. The result may not be reliable. More sample should be collected.
Ex2. The Contingency table below summarized a Civil Exam results collected from white candidates and minority candidates. Is there evidence to support the claim that results are different, so the exam is discriminatory? Test the claim that white and miniority
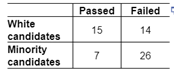
1) H0: White and minority candidates have same chance of passing the exam
Ha: White and minority candidate do not have the same chance of passing the exam
Note: claim is Ha
2) Input the table to Statdisk. Analysis/Contingency Table. Enter significance, select column 1, 2 evaluate.
Output: df = 1 test stat = χ2= 6.28, p-value = 0.0122,
3) Since 0.0122 < 0.05, Reject H0. Conclude the two population has different chance of passing.
4) There is sufficient evidence to support the claim that white and minority candidates do not have the same chance of passing the exam.
5) Check requirement by calculating expected counts.

All expected counts are at least 5, hence chi-square test requirement is satisfied.

