Ch 9.1, 9.3 and 9.4 Hypothesis Test Basic
- Page ID
- 15916
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ch 9.1, 9.3 and 9.4 Hypothesis Test basic
Hypothesis test: (or test of significance) is a procedure based on sample evidence and probability, used to test claim regarding a characteristic of one or more populations. Characteristic of population proportion (p) and mean (μ) will be covered in this course.
To test a hypothesis, you should state a pair of hypotheses, one that represents the claim and the other, its complement. When one of these hypotheses is false, the other must be true. The null hypothesis represents currently acceptable truth.
The alternative hypothesis contains opposing viewpoint.
Basic process of a Hypothesis test (p-value method)
1) Identify the claim.
2) Translate the claim in algebraic symbolic form.
3) Identify the null and alternative hypothesis test and write in symbolic form. H0 and Ha (or H1) are the symbols for the two hypotheses.
4) Select a significant level α. (based on seriousness of making a type I error.)
5) Collect a sample and identify the “Type” of hypothesis test in Ha. Determine the sampling distribution (normal or t).
6) Use calculator to find test statistic and p-value.
7) Make conclusion on H0 based on p-value.
8) Rewrite the conclusion in simple non-technical term and address the original claim.
Part A: Step 1, 2, 3
The claim is about value of a population parameter, we can claim that the parameter is greater, less than, equal to or not equal to a value. (Note: claim of at most, at least is equivalent to claiming equal.)
a) Since the claim is about population parameter, the symbolic form can be: (p or μ) ( \(<, >, \leq, \geq, \neq, = \) ) a claim value.
b) The null hypothesis is the first assumption we use to calculate probability of the sample we obtained,
so the null hypothesis must be of equality form.
c) The alternative hypothesis is the second assumption that must not overlap (or opposite) with the null hypothesis.
H0: (p or μ ) = (a value) ; Ha: (p or μ ) is (\(<, >, \neq \) ) (a value); (a value ) is value that shows up in the claim.
Ex1: Claim that mean body temperature is less than 98.6oF:
claim: μ < 98.6 H0: μ = 98.6 Ha: μ < 98.6
Ex2. Claim that proportion of red M&M is greater than 10%.
claim: p > 0.1; H0: p = 0.1 Ha: p > 0.1
Ex3. Claim that mean IQ scores of college professor is different from 100.
claim: μ = 100; H0: μ = 100 Ha: μ ≠ 100
Ex4. Claim that mean IQ scores of college student is 105.
claim: μ = 105; H0: μ = 105 Ha: μ ≠ 105
Part B: Step 4, 5 and 6:
Common significant level α is 0.05, but if Type 1 error is very undesirable, a lower significant level is better.
If the claim is about p, the sampling distribution is z normal because ![]() is normally distributed.
is normally distributed.
If the claim is about μ, the sampling distribution is t or z normal depending on if σ is known. According to CLT, \( \bar{x} \) is normally distributed if n > 30 or population is Normal.
Obtain a sample and use calculator to find the a “test statistic” and a “p-value”
 Test statistic tells the number of SD the sample is from the assumed parameter value assumed in H0.
Test statistic tells the number of SD the sample is from the assumed parameter value assumed in H0.
P-value tells the probability of getting the sample or worse if the assumption of H0 is true.
P-value are calculated based the “Type” of test:
Types of Hypothesis Test: (determined by looking at Ha)
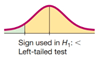 Left-tail test: when Ha has the form of p < value. p-value is left area of test statistic.
Left-tail test: when Ha has the form of p < value. p-value is left area of test statistic.
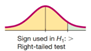 right-tail test: when Ha has the form of p > value. P-value is right area of the test statistic.
right-tail test: when Ha has the form of p > value. P-value is right area of the test statistic.
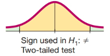 Two-tail test: when Ha has the form of p ≠ value
Two-tail test: when Ha has the form of p ≠ value
p-value is twice of area in left or right area from the test statistic.
The online calculator will calculate test statistic and p-value. https://www.statdisk.com/ #/Analysis/Hypothesis Testing
More detail will be covered in Ch 9.5.
Part C: Step 7 and 8:
The conclusion of a hypothesis test is based on the
Rare Event Rule:
“Based on an assumption, if the observed event is very rare (lower than significant level α), we conclude the assumption is properly not true.”
In a Hypothesis Test, the assumption is H0, the null hypothesis. We determine if the sample is rare based on the assumed claim population characteristic in H0.
Step 7: If p-value ≤ α, reject null hypothesis. Result is Significant!
If p-value > α, fail to reject the null hypothesis.
[ If p-value is low, the null must go.
If p-value is high, the null will fly.]
Step 8: Make conclusion about the claim.
If the p-value ≤ α: use “there is sufficient evidence…”
If the p-value > α, use “there is not sufficient evidence…”
If the claim is H0: Reject H0 implies reject the claim.
If the claim is Ha: Reject H0 implies support the claim.
Or
| Conditions | Conclusion |
|---|---|
| Original claim does not include equality and H0 is rejected. | "There is sufficient evidence to support the claim that .... " |
| Original claim does not include equality and H0 is failed to be rejected. | "There is not sufficient evidence to support the claim that...." |
| Original claim include equality and H0 is rejected. | "There is sufficient evidence to reject the claim that ... " |
| Original claim include equality and H0 is failed to be rejected. | "There is not sufficient evidence to reject the claim that ..." |
Note:
“Not sufficient evidence to reject the claim” implies it is plausible that the claim is true.
“Not sufficient evidence to support the claim” implies the claim may not be true.
Ex1. If significant level = 0.05 and p-value = 0.04, what is the conclusion on H0?
Since 0.04 < 0.05, sample is significant, so reject H0.
Ex2. If significant level = 0.05 and p-value = 0.006, what is the conclusion on H0?
Since 0.006 < 0.05, the sample is significant, so reject H0.
Ex3. If significant level = 0.01 and p-value = 0.03, what is the conclusion on H0
Since 0.03 > 0.01, the sample is not significant, so fail to reject H0.
Ex4. If the claim is Ha and you fail to reject H0, what is the claim conclusion?
There is not enough evidence to support the claim.
Ex5. If the claim is H0 and you reject H0, what is the claim conclusion?
There is sufficient evidence to reject the claim.
All steps practice:
Ex1. Test a claim that body temperature of adult is less than 98.6oF. Use α = 0.05. A random sample of 38 body temperatures (with![]() gives a test statistic of t = –2.56 and p-value of 0.0072.
gives a test statistic of t = –2.56 and p-value of 0.0072.
a) Write the claim and hypothesis,
b) Determine the type of distribution used and “type of hypothesis test.” and significant level.
c) Interpret the meaning of test statistic and p-value.
d) Use p-value to make conclusion about H0 and about the claim.
Answer:
a) Claim: μ < 98.6 H0: μ = 98.6 Ha: μ < 98.6
b) Since μ is the parameter, σ is not known, so use t distribution. Since Ha is “<”, Type of test is left tail.
α = 0.05.
c) Test statistic of t = -2.56 means the sample data is 2.56 standard deviation below μ = 98.6.
p-value of 0.0071 means the probability of having the sample or worse is 0.71% if the real mean is 98.6.
d) Conclusion about H0:
Since p-value < 0.05, reject H0, sample is significant
p-value ≤ α -> use “ there is sufficient evidence”..
Slaim is Ha -> use “ support the claim.”
“There is sufficient evidence to support the claim that mean body temperature is less than 98.6o F.
Ex2: Claim that proportion of red M&M is greater than 10%. Use α = 0.05. A sample (15 red out of 102 M&M candies) gives a test statistic of z = 1.91, p-value = 0.0566.
a) Write the claim and hypothesis,
b) Determine the type of distribution used and “type of hypothesis test” and significant level.
c) Interpret the meaning of test statistic and p-value.
d) Use p-value to make conclusion about H0 and about the claim.
Answer:
a) claim: p > 0.1; H0: p = 0.1; Ha: p > 0.1
b) α = 0.01. Since p is the claim parameter, sampling distribution ![]() is normal, z distribution is used.
is normal, z distribution is used.
Since Ha use p > 0.1, Type of test is right tail test.
α = 0.05.
c) A test statistic of z = 1.91 means the sample proportion is 1.91 times of SD above the mean of p = 0.1.
P-value of 0.0566 means there is 5.66% probability to obtain such as sample if p = 0.1 is true.
d) p-value of 0.0566 > 0.05: fail to reject H0 (sample is not significant because the sample is not a rare event.)
Since p-value > α so use “there is not sufficient evidence” statement.
claim is Ha, use “ support the claim”
Final conclusion: there is not sufficient evidence to support the claim that proportion of red M&M is greater than 10%.
Ex3. Claim that IQ scores of college student has a mean equal to 104. Given that σ for IQ score is 15. A sample of IQ scores from 40 college students ( ![]() = 106, s = 16) give a test statistic z = 0.84 and a
= 106, s = 16) give a test statistic z = 0.84 and a
p-value = 0.1995. Use α = 0.05 to test the claim.
a) Write the claim and hypothesis.
b) Determine the type of distribution used and type of hypothesis test and significant level.
c) Interpret the meaning of test statistic and p-value.
d) Use p-value to make conclusion about H0 and about the claim.
Ans:
a) claim: μ = 104; H0: σ = 104; Ha: μ ≠ 104
b) Since claim parameter is μ but σ is known, so use z-Normal distribution. Since Ha has the form of ≠, the Hypothesis test is a “Two-tail Test”. α = 0.05.
c) Test statistic z = 0.8432 means the sample is 0.84 times of standard deviation from μ = 104.
p-value of 0.1995 means there is 19.95% chance of getting such sample if μ = 104 is true.
d) p-value 0.1995 > 0.05, the sample is not a rare event, fail to reject H0, sample is not significant.
P-value > α so, “Use the wording there is not sufficient evidence.”
Claim is in H0, Use “reject the claim” statement.
Conclusion: There is not sufficient evidence to reject the claim that the college student’s mean IQ is equal to 104. (Conclude that mean IQ for college student could be 104.)

