Ch 8.1 Confidence Interval for Population Mean

Ch 8.1 Confidence Interval for mean with one sample when σ is known

Terms: Population mean: μ,   sample mean:  \( \bar{x} \)  

             sample standard deviation: s,   sample size: n

              Population standard deviation: σ

              Confidence Level:  Clevel,

             Significant Level α: 1 – Clevel  (unlikely)

A) Estimate μ (when σ is given)

Use one sample with size n, \( \bar{x} \) , s or raw data:

\( \fbox{ 1) point estimate of μ: \( \bar{x} \) } \)

\( \fbox{ 2) Interval estimate of μ:  \( \bar{x} - E < \mu < \bar{x} +E \) } \)

 When \( E (EBM) = z_ {\alpha /2} \frac{\sigma}{\sqrt{n}} \)  when σ is given.

Use Online calculator statdisk to find confidence interval of mean when σ is given.

use  https://www.statdisk.com/#

Analysis/Confidence Intervals/Mean one sample/.  If summary statistics (\( \bar{x} \)  , s, n) are given.

Select “use Summary Statistics” tab otherwise use “use data” tab.

Enter C-level, \( \bar{x} \) , s or select with data

Must enter \( \sigma \)  that is given

Output:  E is the margin of error or Error bound for  mean.

Confidence interval estimate is  lower limit < \( \mu \) upper limit 

Note: the requirement for the confidence interval is CLT applies. (n > 30 or X is Normal), sample is SRS.

 

\( z_{\alpha /2 }  \) is the critical value with C-level in the middle

 

 

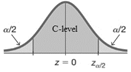
 To find  \( z_{\alpha /2 }  \)

  use Inverse Normal Calculator,  Area = α/2, mean = 0, sd = 1, click above, recalculate.

Explanation:

According to Central Limit Theorem, if n > 30  or X is normal, \( \bar{x} \) has a sampling distribution that is Normal with mean = μ and SD = \( \frac{\sigma}{\sqrt{n}} \) 

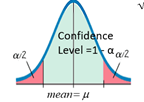Given a C-level, the maximum sampling error of \( \bar{x} \)  from μ is E with a right tail of  area = α/2.

Since standard error is  \( \frac{\sigma}{\sqrt{n}} \), so the range of values

from \( \bar{x} \text{- E  to  }\bar{x} +E \)  should include the real  population mean  \( \mu \) at a confidence level of

C-level.

 

Ex1. Suppose scores on a standardized exam are normally distributed with standard deviation of 35.

A sample of 14 scores are collected with sample mean 137.3 and sample standard deviation 37.2.

a) Use the sample to estimate the population mean score of the standardized test at a 98% confidence level.

Identify: C-level = 0.98 n = 14,  \( \bar{x} \)  = 137.3, s = 37.2,   σ = 35

Statdisk/Analysis/Confidence intervals/Mean one sample/

b) At a confidence level of 98%, what is the significant level and the critical value?

If Clevel = 0.98, α=0.02, use Inverse-Normal calculator with right tail = 0.01,  critical value = \( z_{\alpha /2 }  \) = 2.326

c) A previous study shows that the mean scores was 144.2. Is the population mean score below 144.2?

    No, Since the mean scores can be between 115.5 to 159.06, it cannot be below 144.2.

 

d) Explain what will happen to margin of error E if sample size increase.

    When sample size increase, margin of error should decrease because the formula 

 

e)  Explain what will happen to margin of error E if confidence level increase to 99%.

     When Clevel increase, the critical value will increase so Margin of error will increase.

 

Ex2.  The specific Absorption Rate (SAR) for a cell phone measures the amount of radio frequency energy absorbed by the user’s body when using the handset. The legal SAR level is no more than 1.6 watts per kilogram. The following SAR data are collected from 30 phones. 

1.11, 1.48, 1.43, 1.3, 1.09, 0.455, 1.41, 0.82, 0.78, 1.25, 1.36, 1.34, 1.18, 1.3, 1.26, 1.29, 0.36, 0.52, 1.6, 1.39, 0.74, 0.5, 0.4, 0.867, 0.68, 0.51, 1.13, 0.3, 1.48, 1.38.

a) Use the sample to find the 95% confidence interval of the mean SAR level for all phones given that population standard deviation is σ = 0.337.

 

Ans:  Use Statdisk/Analysis/Confidence Interval/One sample mean/ with data tab

output:

 b) Write the confidence interval in the form of interval notation and +/- notation.

    The interval is  \( \bar{x} \) \pm E. \( \bar{x} \) = (lower limit + upper limit)/2  = 1.02

     The +/- notation is 1.02 \( \pm \) 0.12

c) Can we conclude that the mean SAR level is below the legal allowable value of 1.6?

    Yes, since interval of mean is between 0.90 to 1.14, all these values are below 1.6.

 

d) Find the critical value  \( z_{\alpha /2 }  \)  .

    Since Clevel = 0.95,   \( \alpha \) = 0.05, so \( \alpha /2 \) = 0.025.

    Use Inverse normal calculator, set area = 0.025, mean = 0, sd = 1, click above, recalculate.

    \( z_{\alpha /2 }  \)  = 1.96

e) If we want to decrease the margin of error, what can be done?

   We can increase the margin of error, or decrease Clevel.

 

B) Find sample size n for a given Margin of error (EBM)

From central limit Theorem, we have the equation between E and n is \( E (EBM) = z_ {\alpha /2} \frac{\sigma}{\sqrt{n}} \) . Algebra can be used to show that for a given C-level, E   and σ,

  \( n ={( \frac{z_{\alpha /2}\cdot \sigma }{E}) } ^2 \)

Find sample size by online calculator:

Statdisk.com / Analysis/sample size Determination/ Estimate mean/

Enter Clevel, E, population standard deviation.

Note: when sample size increase, E decrease.

            when E increase, sample size decrease.

Ex3. The population standard deviation of student’s age in a community college is 15 years. If we want to be 95% confidence that the error in confidence interval estimate for mean student's age is within 2 years from the real mean age of all students, how many students must be surveyed?

Use Statdisk/ Analysis / Sample size Determination/

Estimate Mean   Clevel = 0.95,  E = 2, pop. sd = 15

Required sample size = 217.