Ch 3.3 Addition and Multiplication Rule
- Page ID
- 15894
Addition Rule:
Addition Rule are used to find “OR” in a procedure.
P(A or B) = P(A) + P(B) – P(A and B)
If A and B are mutually exclusive: P(A and B) = 0
P(A or B) = P(A)+ P (B) when A, B are mutually exclusive.
Ex1. Toss a 6-face die once, use addition rule method to find P(one or odd).
P(one or odd) = P(one) + P(odd) – P(one and odd)
= 1/6 + 3/6 – 1/6 = 3/6 =0.5
Ex2. Toss a 6-face die once, use addition rule method to find P( one or even)
Because one and even or mutully exclusive, so P (one or even) = P(one) + P(even) = 1/6 + 3/6 = 0.667
Ex3. Use the contingency table below:
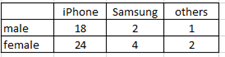
GT = 51
Use addition rule to find P(male or iPhone).
P(male or iPhone) = P(male) + P(iPhone) – P(male and iPhone) = 21/51 + 42/51 – 18/51 = (21+41-18)/51 =45/51 = 0.8823
Multiplication Rule:
Multiplication Rule is used to find probability of two events: A and B.
\( \text{P(A and B)} = P(A) * P(B|A) \)
If A and B are independent, P(B|A) = P(B) so
\( \text{P(A and B)} = P(A) * P(B) \) when A, B are independent.
A result of the multiplication rule gives the formula for conditional probability as:
\(\\text{P(A given B)}=\text{P(A | B)} =\frac{\text{A and B}}{P(B)} \)
Ex1: Given the two-way table below:
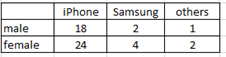
Find P( male |iPhone) = P( male and iPhone)/P(iPhone) = \(\frac{18/51}{42/51} = \frac{18}{42} = 0.4286 \)

