Probability and Independence

For an experiment we define an event to be any collection of possible outcomes. A simple event is an event that consists of exactly one outcome.

• "or" means the union (i.e. either can occur)
• "and" means intersection (i.e. both must occur)

Two events are mutually exclusive if they cannot occur simultaneously. For a Venn diagram, we can tell that two events are mutually exclusive if their regions do not intersect

Definition: Probability

We define probability of an event \(E\) to be to be

\[P(E) = \dfrac{\text{number of simple events within E}}{\text{ total number of possible outcomes}} \nonumber \]

We have the following:

1. \(P(E)\) is always between 0 and 1.
2. The sum of the probabilities of all simple events must be 1.
3. \(P(E) + P(\text{not } E) = 1\)
4. If \(E\) and \(F\) are mutually exclusive then

\[ P(E \text{ or } F) = P(E) + P(F) \nonumber \]

The Difference Between "and" and "or"

If \(E\) and \(F\) are events then we use the terminology

\[ E \text{ and } F \nonumber \]

to mean all outcomes that belong to both \(E\) and \(F\).

We use the terminology

\[E \text{ or } F \nonumber \]

to mean all outcomes that belong to either \(E\) or \(F\).

Below is an example of two sets, \(A\) and \(B\), graphed in a Venn diagram.

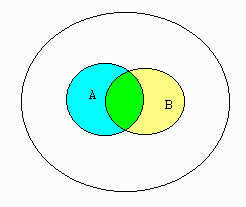
The green area represents \(A\) and \(B\) while all areas with color represent \(A\) or \(B\)

Example \(\PageIndex{1}\)

Our Women's Volleyball team is recruiting for new members. Suppose that a person inquires about the team.

• Let \(E\) be the event that the person is female
• Let \(F\) be the event that the person is a student

then \(E\) and \(F\) represents the qualifications for being a member of the team. Note that \(E\) or \(F\) is not enough.

We define

Definition: Conditional Probability

\[ P(E|F) = \dfrac{P(E \text{ and } F}{P(F)} \nonumber \]

We read the left hand side as "The probability of event \(E\) given event \(F\) occurred."

We call two events independent if the following definitions hold.

Definition: Independence

For independent Events

\[P(E|F) = P(E) \label{1a} \]

Equivalently, we can say that \(E\) and \(F\) are independent if

Definition: The Multiplication Rule

For Independent Events

\[P(E \text{ and } F) = P(E)P(F) \label{1b} \]

Example \(\PageIndex{2}\)

Consider rolling two dice. Let

• \(E\) be the event that the first die is a 3.
• \(F\) be the event that the sum of the dice is an 8.

Then \(E\) and \(F\) means that we rolled a three and then we rolled a 5

This probability is 1/36 since there are 36 possible pairs and only one of them is (3,5)

We have

\[ P(E) = 1/6 \nonumber \]

And note that (2,6),(3,5),(4,4),(5,3), and (6,2) give \(F\)

Hence

\[ P(F) = 5/36 \nonumber \]

We have

\[ P(E) P(F) = (1/6) (5/36) \nonumber \]

which is not 1/36 and we can conclude that \(E\) and \(F\) are not independent.

Exercise \(\PageIndex{2}\)

Test the following two events for independence:

• \(E\) the event that the first die is a 1.
• \(F\) the event that the sum is a 7.

A Counting Rule

For two events, \(E\) and \(F\), we always have

\[ P(E \text{ or } F) = P(E) + P(F) - P(E \text{ and } F) \label{2} \]

Example \(\PageIndex{3}\)

Find the probability of selecting either a heart or a face card from a 52 card deck.

Solution

We let

• \(E\) = the event that a heart is selected
• \(F\) = the event that a face card is selected

then

\[ P(E) = \dfrac{1}{4} \nonumber \]

and

\[ P(F) = \dfrac{3}{13} \nonumber \]

that is, Jack, Queen, or King out of 13 different cards of one kind.

\[ P(E \text{ and } F) = \dfrac{3}{52} \nonumber \]

The counting rule formula (eq. 2) gives

\[ P(E \text{ or } F) = \dfrac{1}{4} + \dfrac{3}{13} - \dfrac{3}{52} = \dfrac{22}{52} = 42\text{%} \nonumber \]

Contributors

• Larry Green (Lake Tahoe Community College)