16.5: Periodicity of Discrete-Time Chains
- Page ID
- 10292
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A state in a discrete-time Markov chain is periodic if the chain can return to the state only at multiples of some integer larger than 1. Periodic behavior complicates the study of the limiting behavior of the chain. As we will see in this section, we can eliminate the periodic behavior by considering the \( d \)-step chain, where \( d \in \N_+ \) is the period, but only at the expense of introducing additional equivalence classes. Thus, in a sense, we can trade one form of complexity for another.
Basic Theory
Definitions and Basic Results
As usual, our starting point is a (time homogeneous) discrete-time Markov chain \( \bs{X} = (X_0, X_1, X_2, \ldots) \) with (countable) state space \( S \) and transition probability matrix \( P \).
The period of state \( x \in S \) is \[ d(x) = \gcd\{n \in \N_+: P^n(x, x) \gt 0 \} \] State \( x \) is aperiodic if \( d(x) = 1 \) and periodic if \( d(x) \gt 1 \).
Thus, starting in \( x \), the chain can return to \( x \) only at multiples of the period \( d \), and \( d \) is the largest such integer. Perhaps the most important result is that period, like recurrence and transience, is a class property, shared by all states in an equivalence class under the to and from relation.
If \( x \leftrightarrow y \) then \( d(x) = d(y) \).
Proof
Suppose that \( x \leftrightarrow y \). The result is trivial if \( x = y \), so let's assume that \( x \neq y \). Recall that there exist \( j, \, k \in \N_+ \) such that \( P^j(x, y) \gt 0 \) and \( P^k(y, x) \gt 0 \). But then \( P^{j+k}(x, x) \ge P^j(x, y) P^k(y, x) \gt 0 \) and hence \( d(x) \mid (j + k) \). Suppose now that \( n \) is a positive integer with \( P^n(y, y) \gt 0 \). Then \( P^{j+k+n}(x, x) \ge P^j(x, y) P^n(y, y) P^k(y, x) \gt 0 \) and hence \( d(x) \mid (j + k + n) \). It follows that \( d(x) \mid n \). From the definition of period, \( d(y) \mid d(x) \). Reversing the roles of \( x \) and \( y \) we also have \( d(x) \mid d(y) \). Hence \( d(x) = d(y) \).
Thus, the definitions of period, periodic, and aperiodic apply to equivalence classes as well as individual states. When the chain is irreducible, we can apply these terms to the entire chain.
Suppose that \( x \in S \). If \( P(x, x) \gt 0 \) then \( x \) (and hence the equivalence class of \( x \)) is aperiodic.
Proof
By assumption, \( 1 \in \{n \in \N_+: P^n(x, x) \gt 0\} \) and hence the greatest common divisor of this set is 1.
The converse is not true, of course. A simple counterexample is given below.
The Cyclic Classes
Suppose now that \( \bs{X} = (X_0, X_1, X_2, \ldots) \) is irreducible and is periodic with period \( d \). There is no real loss in generality in assuming that the chain is irreducible, for if this were not the case, we could simply restrict our attention to one of the irreducible equivalence classes. Our exposition will be easier and cleaner if we recall the congruence equivalence relation modulo \( d \) on \( \Z \), which in turn is based on the divison partial order. For \( n, \, m \in \Z \), \( n \equiv_d m \) if and only if \( d \mid (n - m) \), equivalently \( n - m \) is an integer multiple of \( d \), equivalently \( m \) and \( n \) have the same remainder after division by \( d \). The basic fact that we will need is that \( \equiv_d \) is preserved under sums and differences. That is, if \( m, \, n, \, p, \, q \in \Z \) and if \( m \equiv_d n \) and \( p \equiv_d q \), then \( m + p \equiv_d n + q \) and \( m - p \equiv_d n - q \).
Now, we fix a reference state \( u \in S \), and for \( k \in \{0, 1, \ldots, d - 1\} \), define \[ A_k = \{x \in S: P^{n d + k}(u, x) \gt 0 \text{ for some } n \in \N\} \] That is, \( x \in A_k \) if and only if there exists \( m \in \N \) with \( m \equiv_d k \) and \( P^m(u, x) \gt 0 \).
Suppose that \( x, \, y \in S \).
- If \( x \in A_j \) and \( y \in A_k \) for \( j, \, k \in \{0, 1, \ldots, d - 1\} \) then \( P^n(x, y) \gt 0 \) for some \( n \equiv_d k - j \)
- Conversely, if \( P^n(x, y) \gt 0 \) for some \( n \in \N \), then there exists \( j, \, k \in \{0, 1, \ldots d - 1\} \) such that \( x \in A_j \), \( y \in A_k \) and \( n \equiv_d k - j \).
- The sets \( (A_0, A_1, \ldots, A_{k-1}) \) partition \( S \).
Proof
Suppose first that \( x \in A_k \). By definition, \( u \) leads to \( x \) in \( m \) steps for some \( m \equiv_d k \). Since the chain is irreducible, \( x \) leads back to \( u \), say in \( p \) steps. It follows that \( u \) leads back to \( u \) in \( m + p \) steps. But because \( u \) has period \( d \), we must have \( m + p \equiv_d 0\) and hence \( p \equiv_d -k \).
Next suppose that \( x \in A_j \) and \( y \in A_k \). We know that \( u \) leads to \( x \) in \( m \) steps for some \( m \equiv_d j \), and we now know that \( y \) leads to \( u \) in \( p \) steps for some \( p \equiv_d -k \). Since the chain is irreducible, \( x \) leads to \( y \), say in \( n \) steps. It follows that \( u \) leads back to \( u \) in \( m + n + p \) steps. Again, since \( u \) has period \( d \), \( m + n + p \equiv_d 0 \) and it follows that \( n \equiv_d k - j \)
Next, note that since the chain is irreducible and since \(\{0, 1, \ldots, d - 1\}\) is the set of all remainders modulo \( d \), we must have \( \bigcup_{i=0}^{d-1} A_i = S \). Suppose that \( x, y \in S \) and \( P^n(x, y) \gt 0 \) for some \( n \in \N \). Then \( x \in A_j \) and \( y \in A_k \) for some \(j, \, k \in \{0, 1, \ldots\}\). By the same argument as the last paragraph, we must have \( n \equiv_d k - j \).
All that remains is to show that the sets are disjoint, and that amounts to the same old argument yet again. Suppose that \( x \in A_j \cap A_k \) for some \( j, \, k \in \{0, 1, \ldots, d - 1\} \). Then \( u \) leads to \( x \) in \( m \) steps for some \( m \equiv_d j \) and \( x \) leads to \( u \) in \( n \) steps for some \( n \equiv_d - k \). Hence \( u \) leads back to \( u \) in \( m + n \) steps. Since the chain has period \( d \) we have \( m + n \equiv_d 0 \) and therefore \( j - k \equiv_d 0 \). Since \( j, \, k \in \{0, 1, \ldots, d - 1\} \) it follows that \( j = k \).
\( (A_0, A_1, \ldots, A_{d-1}) \) are the equivalence classes for the \( d \)-step to and from relation \( \underset{d}{\leftrightarrow} \) that governs the \( d \)-step chain \( (X_0, X_d, X_{2 d}, \ldots) \) that has transition matrix \( P^d \).
The sets \( (A_0, A_1, \ldots, A_{d-1}) \) are known as the cyclic classes. The basic structure of the chain is shown in the state diagram below:
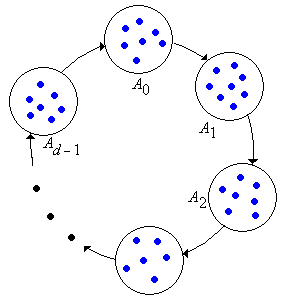
Examples and Special Cases
Finite Chains
Consider the Markov chain with state space \( S = \{a, b, c\} \) and transition matrix \( P \) given below:
\[ P = \left[\begin{matrix} 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{matrix}\right] \]- Sketch the state graph and show that the chain is irreducible.
- Show that the chain is aperiodic.
- Note that \( P(x, x) = 0 \) for all \( x \in S \).
Answer
- The state graph has edge set \( E = \{(a, b), (a, c), (b, c), (b, a)\} \).
- Note that \( P^2(a, a) \gt 0 \) and \( P^3(a, a) \gt 0 \). Hence \( d(a) = 1 \) since 2 and 3 are relatively prime. Since the chain is irreducible, it is aperiodic.
Consider the Markov chain with state space \( S = \{1, 2, 3, 4, 5, 6, 7\} \) and transition matrix \( P \) given below:
\[ P = \left[\begin{matrix} 0 & 0 & \frac{1}{2} & \frac{1}{4} & \frac{1}{4} & 0 & 0 \\ 0 & 0 & \frac{1}{3} & 0 & \frac{2}{3} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{3} & \frac{2}{3} \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & \frac{3}{4} & \frac{1}{4} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & 0 \\ \frac{1}{4} & \frac{3}{4} & 0 & 0 & 0 & 0 & 0 \end{matrix}\right] \]- Sketch the state graph and show that the chain is irreducible.
- Find the period \( d \).
- Find \( P^d \).
- Identify the cyclic classes.
Answer
-
State graph 
- Period 3
- \( P^3 = \left[ \begin{matrix} \frac{71}{192} & \frac{121}{192} & 0 & 0 & 0 & 0 & 0 \\ \frac{29}{72} & \frac{43}{72} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & \frac{7}{18} & \frac{1}{12} & \frac{19}{36} & 0 & 0 \\ 0 & 0 & \frac{19}{48} & \frac{3}{32} & \frac{49}{96} & 0 & 0 \\ 0 & 0 & \frac{13}{32} & \frac{7}{64} & \frac{31}{64} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{157}{299} & \frac{131}{288} \\ 0 & 0 & 0 & 0 & 0 & \frac{37}{64} & \frac{27}{64} \end{matrix} \right] \)
- Cyclic classes: \( \{1, 2\} \), \( \{3, 4, 5\} \), \( \{6, 7\} \)
Special Models
Review the definition of the basic Ehrenfest chain. Show that this chain has period 2, and find the cyclic classes.
Review the definition of the modified Ehrenfest chain. Show that this chain is aperiodic.
Review the definition of the simple random walk on \( \Z^k \). Show that the chain is periodic with period 2, and find the cyclic classes.


