5.35: The Log-Logistic Distribution
- Page ID
- 10468
As the name suggests, the log-logistic distribution is the distribution of a variable whose logarithm has the logistic distribution. The log-logistic distribution is often used to model random lifetimes, and hence has applications in reliability.
The Basic Log-Logistic Distribution
Distribution Functions
The basic log-logistic distribution with shape parameter \( k \in (0, \infty) \) is a continuous distribution on \( [0, \infty) \) with distribution function \( G \) given by \[ G(z) = \frac{z^k}{1 + z^k}, \quad z \in [0, \infty) \] In the special case that \( k = 1 \), the distribution is the standard log-logistic distribution.
Proof
Note that \( G \) is continuous on \( [0, \infty) \) with \( G(0) = 0 \) and \( G(z) \to 1 \) as \( z \to \infty \). Moreover, \[ g(z) = G^\prime(z) = \frac{k z^{k-1}}{(1 + z^k)^2} \gt 0, \quad z \in (0, \infty) \] so \( G \) is strictly increasing on \( [0, \infty) \).
The probability density function function \( g \) is given by \[ g(z) = \frac{k z^{k-1}}{(1 + z^k)^2}, \quad z \in (0, \infty) \]
- If \( 0 \lt k \lt 1 \), \( g \) is decreasing with \( g(z) \to \infty \) as \( z \downarrow 0 \).
- If \( k = 1 \), \( g \) is deceasing with mode \( z = 0 \).
- If \( k \gt 1 \), \( g \) increases and then decreases with mode \( z = \left(\frac{k - 1}{k + 1}\right)^{1/k}. \)
- If \( k \le 1 \), \( g \) is concave upward.
- If \( 1 \lt k \le 2 \), \( g \) is concave downward and then upward, with inflection point at \[ z = \left[\frac{2 (k^2 - 1) + 2 k \sqrt{3(k^2 - 1)}}{(k + 1)(k + 2)}\right]^{1/k} \]
- If \( k \gt 2 \), \( g \) is concave upward then downward then upward again, with inflection points at \[ z = \left[\frac{2 (k^2 - 1) \pm 2 k \sqrt{3(k^2 - 1)}}{(k + 1)(k + 2)}\right]^{1/k} \]
Proof
The PDF \( g = G^\prime \) was computed in the proof of the CDF result. The rest follows from \begin{align} g^{\prime}(z) & = \frac{k z^{k-2}[(k - 1) - (k + 1) z^k]}{(1 + z^k)^3}, \quad z \in (0, \infty) \\ g^{\prime \prime}(z) & = \frac{k z^{k - 3} \left[(k - 1)(k - 2) - 4(k^2 -1) z^k + (k + 1) (k + 2)z^{2 k}\right]}{(1 + z^k)^4}, \quad z \in (0, \infty) \end{align}
So \( g \) has a rich variety of shapes, and is unimodal if \( k \gt 1 \). When \( k \ge 1 \), \( g \) is defined at 0 as well.
Open the special distribution simulator and select the log-logistic distribution. Vary the shape parameter and note the shape of the probability density function. For selected values of the shape parameter, run the simulation 1000 times and compare the empirical density function to the probability density function.
The quantile function \( G^{-1} \) is given by \[ G^{-1}(p) = \left(\frac{p}{1 - p}\right)^{1/k}, \quad p \in [0, 1) \]
- The first quartile is \( q_1 = (1/3)^{1/k} \).
- The median is \( q_2 = 1 \).
- The third quartile is \( q_3 = 3^{1/k} \).
Proof
The formula for \( G^{-1} \) follows from the distribution function by solving \( p = G(z) \) for \( z \) in terms of \( p \).
Recall that \( p \big/ (1 - p) \) is the odds ratio associated with probability \( p \in (0, 1) \). Thus, the quantile function of the basic log-logistic distribution with shape parameter \( k \) is the \( k \)th root of the odds ratio function. In particular, the quantile function of the standard log-logistic distribution is the odds ratio function itself. Also of interest is that the median is 1 for every value of the shape parameter.
Open the special distribution calculator and select the log-logistic distribution. Vary the shape parameter and note the shape of the distribution and probability density functions. For selected values of the shape parameter, computer a few values of the distribution function and the quantile function.
The reliability function \( G^c \) is given by \[ G^c(z) = \frac{1}{1 + z^k}, \quad z \in [0, \infty) \]
Proof
This follows trivially from the distribution function since \( G^c = 1 - G \).
The basic log-logistic distribution has either decreasing failure rate, or mixed decreasing-increasing failure rate, depending on the shape parameter.
The failure rate function \( r \) is given by \[ r(z) = \frac{k z^{k-1}}{1 + z^k}, \quad z \in (0, \infty) \]
- If \( 0 \lt k \le 1 \), \( r \) is decreasing.
- If \( k \gt 1 \), \( r \) decreases and then increases with minimum at \( z = (k - 1)^{1/k} \).
Proof
Recall that the is \( r(z) = g(z) \big/ G^c(z) \) for \(z \in (0, \infty)\) so the formula follows from the PDF and the reliability function above. Parts (a) and (b) follow from \[ r^\prime(z) = \frac{k z^{k-1}[(k - 1) - z^k]}{(1 + z^k)^2}, \quad z \in (0, \infty) \]
If \( k \ge 1 \), \( r \) is defined at 0 also.
Moments
Suppose that \( Z \) has the basic log-logistic distribution with shape parameter \( k \in (0, \infty) \). The moments (about 0) of the \( Z \) have an interesting expression in terms of the beta function \( B \) and in terms of the sine function. The simplest representation is in terms of a new special function constructed from the sine function.
The (normalized) cardinal sine function sinc is defined by \[ \sinc(x) = \frac{\sin(\pi x)}{\pi x}, \quad x \in \R \] where it is understood that \( \sinc(0) = 1 \) (the limiting value).
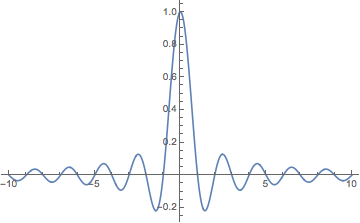
If \( n \ge k \) then \( \E(Z^n) = \infty \). If \( 0 \le n \lt k \) then \[ \E(Z^n) = B\left(1 - \frac{n}{k}, 1 + \frac{n}{k}\right) = \frac{1}{\sinc(n / k)} \]
Proof
Using the PDF, \[ \E(Z^n) = \int_0^\infty z^n \frac{k z^{k-1}}{(1 + z^k)^2} dz \] The substitution \( u = 1 / (1 + z^k) \), \( du = -k z^{k-1}/(1 + z^k)^2 \) gives \[ \E(Z^n) = \int_0^1 (1/u - 1)^{n/k} du = \int_0^1 u^{-n/k} (1 - u)^{n/k} du \] The result now follows from the definition of the beta function.
In particular, we can give the mean and variance.
If \( k \gt 1 \) then \[ \E(Z) = \frac{1}{\sinc(1/k)} \]
If \(k \gt 2 \) then \[ \var(Z) = \frac{1}{\sinc(2 / k)} - \frac{1}{\sinc^2(1 / k)} \]
Open the special distribution simulator and select the log-logistic distribution. Vary the shape parameter and note the size and location of the mean \( \pm \) standard deviation bar. For selected values of the shape parameter, run the simulation 1000 times and compare the empirical mean and standard deviation to the distribution mean and standard deviation.
Related Distributions
The basic log-logistic distribution is preserved under power transformations.
If \( Z \) has the basic log-logistic distribution with shape parameter \( k \in (0, \infty) \) and if \( n \in (0, \infty) \), then \( W = Z^n \) has the basic log-logistic distribution with shape parameter \( k / n \).
Proof
For \( w \in [0, \infty) \), \[ \P(W \le w) = \P(Z \le w^{1/n}) = G\left(w^{1/n}\right) = \frac{w^{k/n}}{1 + w^{k/n}} \] As a function of \( w \), this is the CDF of the basic log-logistic distribution with shape parameter \( k/n \).
In particular, it follows that if \( V \) has the standard log-logistic distribution and \( k \in (0, \infty) \), then \( Z = V^{1/k} \) has the basic log-logistic distribution with shape parameter \( k \).
The log-logistic distribution has the usual connections with the standard uniform distribution by means of the distribution function and the quantile function given above.
Suppose that \( k \in (0, \infty) \).
- If \( U \) has the standard uniform distribution then \( Z = G^{-1}(U) = \left[U \big/ (1 - U)\right]^{1/k} \) has the basic log-logistic distribution with shape parameter \( k \).
- If \( Z \) has the basic log-logistic distribution with shape parameter \( k \) then \( U = G(Z) = Z^k \big/ (1 + Z^k) \) has the standard uniform distribution.
Since the quantile function of the basic log-logistic distribution has a simple closed form, the distribution can be simulated using the random quantile method.
Open the random quantile experiment and select the log-logistic distribution. Vary the shape parameter and note the shape of the distribution and probability density functions. For selected values of the parameter, run the simulation 1000 times and compare the empirical density function, mean, and standard deviation to their distributional counterparts..
Of course, as mentioned in the introduction, the log-logistic distribution is related to the logistic distribution.
Suppose that \( k, \, b \in (0, \infty) \).
- If \( Z \) has the basic log-logistic distribution with shape parameter \( k \) then \( Y = \ln Z \) has the logistic distribution with location parameter 0 and scale parameter \( 1/k \).
- If \( Y \) has the logistic distribution with location parameter \( 0 \) and scale parameter \( b \) then \( Z = e^Y \) has the basic log-logistic distribution with shape parameter \( 1 / b \).
Proof
- Suppose first that \( Z \) has the standard log-logistic distribution. Then \[ \P(Y \le y) = \P\left(Z \le e^y\right) = \frac{e^y}{1 + e^y}, \quad y \in \R \] and as a function of \( y \), this is the CDF of the standard logistic distribution. Suppose now that \( Z \) has the basic log-logistic distribution with shape parameter \( k \). From the power result, we can take \( Z = W^{1/k} \) where \( W \) has the standard log-logistic distribution. Then \( Y = \ln Z = \frac{1}{k} \ln W \). But \( \ln(W) \) has the standard logistic distribution, and hence \( \frac{1}{k} \ln W \) has the logistic distribution with location parameter \( 0 \) and scale parameter \( 1/k \)
- Suppose first that \( Y \) has the standard logistic distribution. Then \[ \P(Z \le z) = \P[Y \le \ln(z)] = \frac{e^{\ln z}}{1 + e^{\ln z }} = \frac{z}{1 + z}, \quad z \in (0, \infty) \] and as a function of \( z \), this is the CDF of the standard log-logistic distribution. Suppose now that \( Y \) has the logistic distribution with location parameter 0 and scale parameter \( b \). We can take \( Y = b V \) where \( V \) has the standard logistic distribution. Hence \( Z = e^Y = e^{b V} = \left(e^V\right)^b \). But \( e^V \) has the standard log-logistic distribution, and again by the power result \( \left(e^V\right)^b \) has the log-logistic distribution with shape parameter \( 1 / b \).
As a special case, (and as noted in the proof), if \( Z \) has the standard log-logistic distribution, then \( Y = \ln Z \) has the standard logistic distribution, and if \( Y \) has the standard logistic distribution, then \( Z = e^Y \) has the standard log-logistic distribution.
The standard log-logistic distribution is the same as the standard beta prime distribution.
Proof
The PDF of the standard log-logistic distribution is \( g(z) = 1 \big/ (1 + z)^2 \) for \( z \in [0, \infty) \), which is the same as the PDF of the standard beta prime distribution.
Of course, limiting distributions with respect to parameters are always interesting.
The basic log-logistic distribution with shape parameter \( k \in (0, \infty) \) converges to point mass at 1 as \( k \to \infty \).
Proof from the definition
Note that the distribution function satisfies \( G(z) \to 0 \) as \( k \to \infty \) for \( 0 \le z \lt 1 \), \( G(1) = \frac{1}{2} \) for all \( k \gt 1 \), and \( G(z) \to 1 \) as \( k \to \infty \) for \( z \gt 1 \). Except for the point of discontinuity \( z = 1 \), the limiting values are the distribution function of point mass at 1.
Random variable proof
Suppose that \( V \) has the standard log-logistic distribution, and for \( k \in (0, \infty) \), let \( Z_k = V^{1/k} \), so that \( Z_k \) has the basic log-logistic distribution with shape parameter \( k \). The event \( \{V \gt 0\} \) has probability 1, and on this event, \( Z_k \to 1 \) as \( k \to \infty \). But convergence with probability 1 implies convergence in distribution.
The General Log-Logistic Distribution
The basic log-logistic distribution is generalized, like so many distributions on \( [0, \infty) \), by adding a scale parameter. Recall that a scale transformation often corresponds to a change of units (gallons into liters, for example), and so such transformations are of basic importance.
If \( Z \) has the basic log-logistic distribution with shape parameter \( k \in (0, \infty) \) and if \( b \in (0, \infty) \) then \( X = b Z \) has the log-logistic distribution with shape parameter \( k \) and scale parameter \( b \).
Distribution Functions
Suppose that \(X\) has the log-logistic distribution with shape parameter \(k \in (0, \infty)\) and scale parameter \(b \in (0, \infty)\).
\( X \) has distribution function \( F \) given by \[ F(x) = \frac{x^k}{b^k + x^k}, \quad x \in [0, \infty) \]
Proof
Recall that \( F(x) = G(x / b) \) where \( G \) is the distribution function of the basic log-logistic distribution with shape parameter \( k \).
\( X \) has probability density function \( f \) given by \[ f(x) = \frac{b^k k x^{k-1}}{(b^k + x^k)^2}, \quad x \in (0, \infty) \] When \( k \ge 1 \), \( f \) is defined at 0 also. \( f \) satisfies the following properties:
- If \( 0 \lt k \lt 1 \), \( f \) is decreasing with \( f(x) \to \infty \) as \( x \downarrow 0 \).
- If \( k = 1 \), \( f \) is deceasing with mode \( x = 0 \).
- If \( k \gt 1 \), \( f \) increases and then decreases with mode \( x = b \left(\frac{k - 1}{k + 1}\right)^{1/k}. \)
- If \( k \le 1 \), \( f \) is concave upward.
- If \( 1 \lt k \le 2 \), \( f \) is concave downward and then upward, with inflection point at \[ x = b \left[\frac{2 (k^2 - 1) + 2 k \sqrt{3(k^2 - 1)}}{(k + 1)(k + 2)}\right]^{1/k} \]
- If \( k \gt 2 \), \( f \) is concave upward then downward then upward again, with inflection points at \[ x = b \left[\frac{2 (k^2 - 1) \pm 2 k \sqrt{3(k^2 - 1)}}{(k + 1)(k + 2)}\right]^{1/k} \]
Proof
Recall that \( f(x) = \frac{1}{b} g\left(\frac{x}{b}\right) \) where \( g \) is the probability density function of the basic log-logistic distribution with shape parameter \(k\). Also of course, \( f = F^\prime \).
Open the special distribution simulator and select the log-logistic distribution. Vary the shape and scale parameters and note the shape of the probability density function. For selected values of the parameters, run the simulation 1000 times and compare the empirical density function to the probability density function.
\( X \) has quantile function \( F^{-1} \) given by \[ F^{-1}(p) = b \left(\frac{p}{1 - p}\right)^{1/k}, \quad p \in [0, 1) \]
- The first quartile is \( q_1 = b (1/3)^{1/k} \).
- The median is \( q_2 = b \).
- The third quartile is \( q_3 = b 3^{1/k} \).
Proof
Recall that \( F^{-1}(p) = b G^{-1}(p) \) for \( p \in [0, 1) \) where \( G^{-1} \) is the quantlie function of the basic log-logistic distribution with shape parameter \(k\).
Open the special distribution calculator and select the log-logistic distribution. Vary the shape and sclae parameters and note the shape of the distribution and probability density functions. For selected values of the parameters, computer a few values of the distribution function and the quantile function.
\( X \) has reliability function \( F^c \) given by \[ F^c(x) = \frac{b^k}{b^k + x^k}, \quad x \in [0, \infty) \]
Proof
This follows trivially from the distribution function, since \( F^c = 1 - F \).
The log-logistic distribution has either decreasing failure rate, or mixed decreasing-increasing failure rate, depending on the shape parameter.
\( X \) has failure rate function \( R \) given by \[ R(x) = \frac{k x^{k-1}}{b^k + x^k}, \quad x \in (0, \infty) \]
- If \( 0 \lt k \le 1 \), \( R \) is decreasing.
- If \( k \gt 1 \), \( R \) decreases and then increases with minimum at \( x = b (k - 1)^{1/k} \).
Proof
Recall that \( R(x) = \frac{1}{b} r\left(\frac{x}{b}\right) \) where \( r \) is the failure rate function of the basic log-logistic distribution with shape parameter \(k\). Also, \( R = f \big/ F^c \) where \( f \) is the PDF and \( F^c \) is the reliability function,.
Moments
Suppose again that \( X \) has the log-logistic distribution with shape parameter \( k \in (0, \infty) \) and scale parameter \( b \in (0, \infty) \). The moments of \( X \) can be computed easily from the representation \( X = b Z \) where \( Z \) has the basic log-logistic distribution with shape parameter \( k \). Again, the expressions are simplest in terms of the beta function \( B \) and in terms of the normalized cardinal sine function sinc.
If \( n \ge k \) then \( \E(X^n) = \infty \). If \( 0 \le n \lt k \) then \[ \E(X^n) = b^n B\left(1 - \frac{n}{k}, 1 + \frac{n}{k}\right) = \frac{b^n}{\sinc(n / k)} \]
If \( k \gt 1 \) then \[ \E(X) = \frac{b}{\sinc(1/k)} \]
If \(k \gt 2 \) then \[ \var(X) = b^2 \left[\frac{1}{\sinc(2 / k)} - \frac{1}{\sinc^2(1 / k)} \right] \]
Open the special distribution simulator and select the log-logistic distribution. Vary the shape and scale parameters and note the size and location of the mean/standard deviation bar. For selected values of the parameters, run the simulation 1000 times compare the empirical mean and standard deviation to the distribution mean and standard deviation.
Related Distributions
Since the log-logistic distribution is a scale family for each value of the shape parameter, it is trivially closed under scale transformations.
If \( X \) has the log-logistic distribution with shape parameter \( k \in (0, \infty) \) and scale parameter \( b \in (0, \infty) \), and if \( c \in (0, \infty) \), then \( Y = c X \) has the log-logistic distribution with shape parameter \( k \) and scale parameter \( b c \).
Proof
By definition we can take \(X = b Z\) where \(Z\) has the basic log-logistic distribution with shape parameter \(k\). But then \(Y = c X = (b c) Z\).
The log-logistic distribution is preserved under power transformations.
If \( X \) has the log-logistic distribution with shape parameter \( k \in (0, \infty) \) and scale parameter \( b \in (0, \infty) \), and if \( n \in (0, \infty) \), then \( Y = X^n \) has the log-logistic distribution with shape parameter \( k / n \) and scale parameter \( b^n \).
Proof
Again we can take \( X = b Z \) where \( Z \) has the basic log-logistic distribution with shape parameter \( k \). Then \( X^n = b^n Z^n \). But by the power result for the standard distribution, \( Z^n \) has the basic log-logistic distribution with shape parameter \( k / n \) and hence \( X \) has the log-logistic distribution with shape parameter \( k / n \) and scale parameter \( b^n \).
In particular, if \( V \) has the standard log-logistic distribution, then \( X = b V^{1/k} \) has the log-logistic distribution with shape parameter \( k \) and scale parameter \( b \).
As before, the log-logistic distribution has the usual connections with the standard uniform distribution by means of the distribution function and the quantile function computed above.
Suppose that \( k, \, b \in (0, \infty) \).
- If \( U \) has the standard uniform distribution then \( X = F^{-1}(U) = b \left[U \big/ (1 - U)\right]^{1/k} \) has the log-logistic distribution with shape parameter \( k \) and scale parameter \( b \).
- If \( X \) has the log-logistic distribution with shape parameter \( k \) and scale parameter \( b \), then \( U = F(X) = X^k \big/ (b^k + X^k) \) has the standard uniform distribution.
Again, since the quantile function of the log-logistic distribution has a simple closed form, the distribution can be simulated using the random quantile method.
Open the random quantile experiment and select the log-logistic distribution. Vary the shape and scale parameters and note the shape and location of the distribution and probability density functions. For selected values of the parameters, run the simulation 1000 times and compare the empirical density function, mean and standard deviation to their distributional counterparts.
Again, the logarithm of a log-logistic variable has the logistic distribution.
Suppose that \( k, \, b, \, c \in (0, \infty) \) and \( a \in \R \).
- If \( X \) has the log-logistic distribution with shape parameter \( k \) and scale parameter \( b \) then \( Y = \ln X \) has the logistic distribution with location parameter \( \ln b \) and scale parameter \( 1 / k \).
- If \( Y \) has the logistic distribution with location parameter \( a \) and scale parameter \( c \) then \( X = e^Y \) has the log-logistic distribution with shape parameter \( 1/c \) and scale parameter \( e^a \).
Proof
- As noted above, we can take \( X = b V^{1/k} \) where \( V \) has the standard log-logistic distribution. Then \( Y = \ln X = \ln b + \frac{1}{k} \ln V \). But by the corresponding result for the basic distribution, \( \ln V \) has the standard logistic distribution, so \( Y \) has the logistic distribution with location parameter \( \ln b \) and scale parameter \( 1/k \).
- We can take \( Y = a + c U \) where \( U \) has the standard logistic distribution. Hence \( X = e^Y = e^a e^{c U} = e^a \left(e^U\right)^c \). But by the result corresponding result for the standard distribution, \( e^U \) has the standard log-logistic distribution so \( X \) has the log-logistic distribution with shape parameter \( 1/c \) and scale parameter \( e^a \).
Once again, the limiting distribution is also of interest.
For fixed \( b \in (0, \infty) \), the log-logistic distribution with shape parameter \( k \in (0, \infty) \) and scale parameter \( b \) converges to point mass at \( b \) as \( k \to \infty \).
Proof
If \( X \) has the log-logistic distribution with shape parameter \( k \) and scale parameter \( b \), then as usual, we can write \( X = b Z \) where \( Z \) has the basic log-logistic distribution with shape parameter \( k \). From the limit result for the basic distribution, we know that the distribution of \( Z \) converges to point mass at 1 as \( k \to \infty \), so it follows by the continuity theorem that the distribution of \( X \) converges to point mass at \( b \) as \( k \to \infty \).


