4.6: Generating Functions
- Page ID
- 10161
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As usual, our starting point is a random experiment modeled by a probability sace \((\Omega, \mathscr F, \P)\). A generating function of a real-valued random variable is an expected value of a certain transformation of the random variable involving another (deterministic) variable. Most generating functions share four important properties:
- Under mild conditions, the generating function completely determines the distribution of the random variable.
- The generating function of a sum of independent variables is the product of the generating functions
- The moments of the random variable can be obtained from the derivatives of the generating function.
- Ordinary (pointwise) convergence of a sequence of generating functions corresponds to the special convergence of the corresponding distributions.
Property 1 is perhaps the most important. Often a random variable is shown to have a certain distribution by showing that the generating function has a certain form. The process of recovering the distribution from the generating function is known as inversion. Property 2 is frequently used to determine the distribution of a sum of independent variables. By contrast, recall that the probability density function of a sum of independent variables is the convolution of the individual density functions, a much more complicated operation. Property 3 is useful because often computing moments from the generating function is easier than computing the moments directly from the probability density function. The last property is known as the continuity theorem. Often it is easer to show the convergence of the generating functions than to prove convergence of the distributions directly.
The numerical value of the generating function at a particular value of the free variable is of no interest, and so generating functions can seem rather unintuitive at first. But the important point is that the generating function as a whole encodes all of the information in the probability distribution in a very useful way. Generating functions are important and valuable tools in probability, as they are in other areas of mathematics, from combinatorics to differential equations.
We will study the three generating functions in the list below, which correspond to increasing levels of generality. The fist is the most restrictive, but also by far the simplest, since the theory reduces to basic facts about power series that you will remember from calculus. The third is the most general and the one for which the theory is most complete and elegant, but it also requires basic knowledge of complex analysis. The one in the middle is perhaps the one most commonly used, and suffices for most distributions in applied probability.
We will also study the characteristic function for multivariate distributions, although analogous results hold for the other two types. In the basic theory below, be sure to try the proofs yourself before reading the ones in the text.
Basic Theory
The Probability Generating Function
For our first generating function, assume that \(N\) is a random variable taking values in \(\N\).
The probability generating function \(P\) of \(N\) is defined by \[ P(t) = \E\left(t^N\right) \] for all \(t \in \R\) for which the expected value exists in \( \R \).
That is, \( P(t) \) is defined when \( \E\left(|t|^N\right) \lt \infty \). The probability generating function can be written nicely in terms of the probability density function.
Suppose that \(N\) has probability density function \(f\) and probability generating function \(P\). Then \[ P(t) = \sum_{n=0}^\infty f(n) t^n, \quad t \in (-r, r) \] where \( r \in [1, \infty] \) is the radius of convergence of the series.
Proof
The expansion follows from the discrete change of variables theorem for expected value. Note that the series is a power series in \( t \), and hence by basic calculus, converges absolutely for \( t \in (-r, r) \) where \( r \in [0, \infty] \) is the radius of convergence. But since \( \sum_{n=0}^\infty f(n) = 1 \) we must have \( r \ge 1 \), and the series converges absolutely at least for \( t \in [-1, 1] \).
In the language of combinatorics, \(P\) is the ordinary generating function of \(f\). Of course, if \( N \) just takes a finite set of values in \( \N \) then \( r = \infty \). Recall from calculus that a power series can be differentiated term by term, just like a polynomial. Each derivative series has the same radius of convergence as the original series (but may behave differently at the endpoints of the interval of convergence). We denote the derivative of order \(n\) by \(P^{(n)}\). Recall also that if \(n \in \N\) and \(k \in \N\) with \(k \le n\), then the number of permutations of size \(k\) chosen from a population of \(n\) objects is \[ n^{(k)} = n (n - 1) \cdots (n - k + 1) \] The following theorem is the inversion result for probability generating functions: the generating function completely determines the distribution.
Suppose again that \(N\) has probability density function \(f\) and probability generating function \(P\). Then \[ f(k) = \frac{P^{(k)}(0)}{k!}, \quad k \in \N \]
Proof
This is a standard result from the theory of power series. Differentiating \( k \) times gives \( P^{(k)}(t) = \sum_{n=k}^\infty n^{(k)} f(n) t^{n-k} \) for \( t \in (-r, r) \). Hence \( P^{(k)}(0) = k^{(k)} f(k) = k! f(k) \)
Our next result is not particularly important, but has a certain curiosity.
\(\P(N \text{ is even}) = \frac{1}{2}\left[1 + P(-1)\right]\).
Proof
Note that \[ P(1) + P(-1) = \sum_{n=0}^\infty f(n) + \sum_{n=0}^\infty (-1)^n f(n) = 2 \sum_{k=0}^\infty f(2 k) = 2 \P(N \text{ is even }) \] We can combine the two sum since we know that the series converge absolutely at 1 and \(-1\).
Recall that the factorial moment of \( N \) of order \( k \in \N \) is \( \E\left[N^{(k)}\right] \). The factorial moments can be computed from the derivatives of the probability generating function. The factorial moments, in turn, determine the ordinary moments about 0 (sometimes referred to as raw moments).
Suppose that the radius of convergence \(r \gt 1\). Then \(P^{(k)}(1) = \E\left[N^{(k)}\right]\) for \(k \in \N\). In particular, \(N\) has finite moments of all orders.
Proof
As before, \( P^{(k)}(t) = \sum_{n=k}^\infty n^{(k)} f(n) t^{n-k} \) for \( t \in (-r, r) \). Hence if \( r \gt 1 \) then \( P^{(k)}(1) = \sum_{n=k}^\infty n^{(k)} f(n) = \E\left[N^{(k)}\right] \)
Suppose again that \( r \gt 1 \). Then
- \(\E(N) = P^\prime(1)\)
- \(\var(N) = P^{\prime \prime}(1) + P^\prime(1)\left[1 - P^\prime(1)\right]\)
Proof
- \( \E(N) = \E\left[N^{(1)}\right] = P^\prime(1) \).
- \( \E\left(N^2\right) = \E[N (N - 1)] + \E(N) = \E\left[N^{(2)}\right] + \E(N) = P^{\prime\prime}(1) + P^\prime(1) \). Hence from (a), \( \var(N) = P^{\prime\prime}(1) + P^\prime(1) - \left[P^\prime(1)\right]^2 \).
Suppose that \(N_1\) and \(N_2\) are independent random variables taking values in \(\N\), with probability generating functions \(P_1\) and \(P_2\) having radii of convergence \( r_1 \) and \( r_2 \), respectively. Then the probability generating function \( P \) of \(N_1 + N_2\) is given by \(P(t) = P_1(t) P_2(t)\) for \( \left|t\right| \lt r_1 \wedge r_2 \).
Proof
Recall that the expected product of independent variables is the product of the expected values. Hence \[ P(t) = \E\left(t^{N_1 + N_2}\right) = \E\left(t^{N_1} t^{N_2}\right) = \E\left(t^{N_1}\right) \E\left(t^{N_2}\right) = P_1(t) P_2(t), \quad \left|t\right| \lt r_1 \wedge r_2 \]
The Moment Generating Function
Our next generating function is defined more generally, so in this discussion we assume that the random variables are real-valued.
The moment generating function of \(X\) is the function \(M\) defined by \[ M(t) = \E\left(e^{tX}\right), \quad t \in \R \]
Note that since \(e^{t X} \ge 0\) with probability 1, \(M(t)\) exists, as a real number or \(\infty\), for any \(t \in \R\). But as we will see, our interest will be in the domain where \( M(t) \lt \infty \).
Suppose that \(X\) has a continuous distribution on \(\R\) with probability density function \(f\). Then \[ M(t) = \int_{-\infty}^\infty e^{t x} f(x) \, dx \]
Proof
This follows from the change of variables theorem for expected value.
Thus, the moment generating function of \(X\) is closely related to the Laplace transform of the probability density function \(f\). The Laplace transform is named for Pierre Simon Laplace, and is widely used in many areas of applied mathematics, particularly differential equations. The basic inversion theorem for moment generating functions (similar to the inversion theorem for Laplace transforms) states that if \(M(t) \lt \infty\) for \(t\) in an open interval about 0, then \(M\) completely determines the distribution of \(X\). Thus, if two distributions on \(\R\) have moment generating functions that are equal (and finite) in an open interval about 0, then the distributions are the same.
Suppose that \(X\) has moment generating function \(M\) that is finite in an open interval \( I \) about 0. Then \(X\) has moments of all orders and \[ M(t) = \sum_{n=0}^\infty \frac{\E\left(X^n\right)}{n!} t^n, \quad t \in I \]
Proof
Under the hypotheses, the expected value operator can be interchanged with the infinite series for the exponential function: \[ M(t) = \E\left(e^{t X}\right) = \E\left(\sum_{n=0}^\infty \frac{X^n}{n!} t^n\right) = \sum_{n=0}^\infty \frac{\E(X^n)}{n!} t^n, \quad t \in I \] The interchange is a special case of Fubini's theorem, named for Guido Fubini. For more details see the advanced section on properties of the integral in the chapter on Distributions.
So under the finite assumption in the last theorem, the moment generating function, like the probability generating function, is a power series in \( t \).
Suppose again that \( X \) has moment generating function \( M \) that is finite in an open interval about 0. Then \(M^{(n)}(0) = \E\left(X^n\right)\) for \(n \in \N\)
Proof
This follows by the same argument as above for the PGF: \( M^{(n)}(0) / n! \) is the coefficient of order \( n \) in the power series above, namely \( \E\left(X^n\right) / n! \). Hence \( M^{(n)}(0) = \E\left(X^n\right) \).
Thus, the derivatives of the moment generating function at 0 determine the moments of the variable (hence the name). In the language of combinatorics, the moment generating function is the exponential generating function of the sequence of moments. Thus, a random variable that does not have finite moments of all orders cannot have a finite moment generating function. Even when a random variable does have moments of all orders, the moment generating function may not exist. A counterexample is constructed below.
For nonnegative random variables (which are very common in applications), the domain where the moment generating function is finite is easy to understand.
Suppose that \( X \) takes values in \( [0, \infty) \) and has moment generating function \( M \). If \( M(t) \lt \infty \) for \( t \in \R \) then \( M(s) \lt \infty \) for \( s \le t \).
Proof
Since \( X \ge 0 \), if \( s \le t \) then \( s X \le t X \) and hence \( e^{s X} \le e^{t X} \). Hence \( \E\left(e^{s X}\right) \le \E\left(e^{t X} \right) \).
So for a nonnegative random variable, either \( M(t) \lt \infty \) for all \( t \in \R \) or there exists \( r \in (0, \infty) \) such that \( M(t) \lt \infty \) for \( t \lt r \). Of course, there are complementary results for non-positive random variables, but such variables are much less common. Next we consider what happens to the moment generating function under some simple transformations of the random variables.
Suppose that \(X\) has moment generating function \(M\) and that \(a, \, b \in \R\). The moment generating function \( N \) of \(Y = a + b X\) is given by \(N(t) = e^{a t} M(b t)\) for \( t \in \R \).
Proof
\( \E\left[e^{t (a + b X)}\right] = \E\left(e^{t a} e^{t b X}\right) = e^{t a} \E\left[e^{(t b) X}\right] = e^{a t} M(b t) \) for \(t \in \R).
Recall that if \( a \in \R \) and \( b \in (0, \infty) \) then the transformation \( a + b X \) is a location-scale transformation on the distribution of \( X \), with location parameter \(a\) and scale parameter \(b\). Location-scale transformations frequently arise when units are changed, such as length changed from inches to centimeters or temperature from degrees Fahrenheit to degrees Celsius.
Suppose that \(X_1\) and \(X_2\) are independent random variables with moment generating functions \(M_1\) and \(M_2\) respectively. The moment generating function \( M \) of \(Y = X_1 + X_2\) is given by \(M(t) = M_1(t) M_2(t)\) for \( t \in \R \).
Proof
As with the PGF, the proof for the MGF relies on the law of exponents and the fact that the expected value of a product of independent variables is the product of the expected values: \[ \E\left[e^{t (X_1 + X_2)}\right] = \E\left(e^{t X_1} e^{t X_2}\right) = \E\left(e^{t X_1}\right) \E\left(e^{t X_2}\right) = M_1(t) M_2(t), \quad t \in \R \]
The probability generating function of a variable can easily be converted into the moment generating function of the variable.
Suppose that \(X\) is a random variable taking values in \(\N\) with probability generating function \(G\) having radius of convergence \( r \). The moment generating function \( M \) of \(X\) is given by \(M(t) = G\left(e^t\right)\) for \( t \lt \ln(r) \).
Proof
\( M(t) = \E\left(e^{t X}\right) = \E\left[\left(e^t\right)^X\right] = G\left(e^t\right) \) for \( e^t \lt r \).
The following theorem gives the Chernoff bounds, named for the mathematician Herman Chernoff. These are upper bounds on the tail events of a random variable.
If \(X\) has moment generating function \(M\) then
- \(\P(X \ge x) \le e^{-t x} M(t)\) for \(t \gt 0\)
- \(\P(X \le x) \le e^{-t x} M(t)\) for \(t \lt 0\)
Proof
- From Markov's inequality, \(\P(X \ge x) = \P\left(e^{t X} \ge e^{t x}\right) \le \E\left(e^{t X}\right) \big/ e^{t x} = e^{-t x} M(t) \) if \(t \gt 0\).
- Similarly, \(\P(X \le x) = \P\left(e^{t X} \ge e^{t x}\right) \le e^{-t x} M(t) \) if \(t \lt 0\).
Naturally, the best Chernoff bound (in either (a) or (b)) is obtained by finding \(t\) that minimizes \(e^{-t x} M(t)\).
The Characteristic Function
Our last generating function is the nicest from a mathematical point of view. Once again, we assume that our random variables are real-valued.
The characteristic function of \(X\) is the function \( \chi \) defined by by \[ \chi(t) = \E\left(e^{i t X}\right) = \E\left[\cos(t X)\right] + i \E\left[\sin(t X)\right], \quad t \in \R \]
Note that \(\chi\) is a complex valued function, and so this subsection requires some basic knowledge of complex analysis. The function \(\chi\) is defined for all \(t \in \R\) because the random variable in the expected value is bounded in magnitude. Indeed, \(\left|e^{i t X}\right| = 1\) for all \(t \in \R\). Many of the properties of the characteristic function are more elegant than the corresponding properties of the probability or moment generating functions, because the characteristic function always exists.
If \(X\) has a continuous distribution on \(\R\) with probability density function \(f\) and characteristic function \( \chi \) then \[ \chi(t) = \int_{-\infty}^{\infty} e^{i t x} f(x) dx, \quad t \in \R \]
Proof
This follows from the change of variables theorem for expected value, albeit a complex version.
Thus, the characteristic function of \(X\) is closely related to the Fourier transform of the probability density function \(f\). The Fourier transform is named for Joseph Fourier, and is widely used in many areas of applied mathematics.
As with other generating functions, the characteristic function completely determines the distribution. That is, random variables \(X\) and \(Y\) have the same distribution if and only if they have the same characteristic function. Indeed, the general inversion formula given next is a formula for computing certain combinations of probabilities from the characteristic function.
Suppose again that \( X \) has characteristic function \( \chi \). If \( a, \, b \in \R \) and \(a \lt b\) then \[ \int_{-n}^n \frac{e^{-i a t} - e^{- i b t}}{2 \pi i t} \chi(t) \, dt \to \P(a \lt X \lt b) + \frac{1}{2}\left[\P(X = b) - \P(X = a)\right] \text{ as } n \to \infty \]
The probability combinations on the right side completely determine the distribution of \(X\). A special inversion formula holds for continuous distributions:
Suppose that \(X\) has a continuous distribution with probability density function \(f\) and characteristic function \( \chi \). At every point \(x \in \R\) where \(f\) is differentiable, \[ f(x) = \frac{1}{2 \pi} \int_{-\infty}^\infty e^{-i t x} \chi(t) \, dt \]
This formula is essentially the inverse Fourrier transform. As with the other generating functions, the characteristic function can be used to find the moments of \(X\). Moreover, this can be done even when only some of the moments exist.
Suppose again that \( X \) has characteristic function \( \chi \). If \(n \in \N_+\) and \(\E\left(\left|X^n\right|\right) \lt \infty\). Then \[ \chi(t) = \sum_{k=0}^n \frac{\E\left(X^k\right)}{k!} (i t)^k + o(t^n) \] and therefore \(\chi^{(n)}(0) = i^n \E\left(X^n\right)\).
Details
Recall that the last term is a generic function that satisfies \(o(t^n) / t^n \to 0\) as \(t \to \infty\).
Next we consider how the characteristic function is changed under some simple transformations of the variables.
Suppose that \(X\) has characteristic function \(\chi\) and that \(a, \, b \in \R\). The characteristic function \( \psi \) of \(Y = a + b X\) is given by \(\psi(t) = e^{i a t} \chi(b t)\) for \( t \in \R \).
Proof
The proof is just like the one for the MGF: \( \psi(t) = \E\left[e^{i t (a + b X)}\right] = \E\left(e^{i t a} e^{i t b X}\right) = e^{i t a} \E\left[e^{i (t b) X}\right] = e^{i a t} \chi(b t) \) for \(t \in \R\).
Suppose that \(X_1\) and \(X_2\) are independent random variables with characteristic functions \(\chi_1\) and \(\chi_2\) respectively. The characteristic function \( \chi \) of \(Y = X_1 + X_2\) is given by \(\chi(t) = \chi_1(t) \chi_2(t)\) for \( t \in \R \).
Proof
Again, the proof is just like the one for the MGF: \[ \chi(t) = \E\left[e^{i t (X_1 + X_2)}\right] = \E\left(e^{i t X_1} e^{i t X_2}\right) = \E\left(e^{i t X_1}\right) \E\left(e^{i t X_2}\right) = \chi_1(t) \chi_2(t), \quad t \in \R \]
The characteristic function of a random variable can be obtained from the moment generating function, under the basic existence condition that we saw earlier.
Suppose that \(X\) has moment generating function \(M\) that satisfies \(M(t) \lt \infty\) for \(t\) in an open interval \(I\) about 0. Then the characteristic function \(\chi\) of \(X\) satisfies \(\chi(t) = M(i t)\) for \(t \in I\).
The final important property of characteristic functions that we will discuss relates to convergence in distribution. Suppose that \((X_1, X_2, \ldots)\) is a sequence of real-valued random with characteristic functions \((\chi_1, \chi_2, \ldots)\) respectively. Since we are only concerned with distributions, the random variables need not be defined on the same probability space.
The Continuity Theorem
- If the distribution of \(X_n\) converges to the distribution of a random variable \(X\) as \(n \to \infty\) and \(X\) has characteristic function \(\chi\), then \(\chi_n(t) \to \chi(t)\) as \(n \to \infty\) for all \(t \in \R\).
- Conversely, if \(\chi_n(t)\) converges to a function \(\chi(t)\) as \(n \to \infty\) for \(t\) in an open interval about 0, and if \(\chi\) is continuous at 0, then \(\chi\) is the characteristic function of a random variable \(X\), and the distribution of \(X_n\) converges to the distribution of \(X\) as \(n \to \infty\).
There are analogous versions of the continuity theorem for probability generating functions and moment generating functions. The continuity theorem can be used to prove the central limit theorem, one of the fundamental theorems of probability. Also, the continuity theorem has a straightforward generalization to distributions on \(\R^n\).
The Joint Characteristic Function
All of the generating functions that we have discussed have multivariate extensions. However, we will discuss the extension only for the characteristic function, the most important and versatile of the generating functions. There are analogous results for the other generating functions. So in this discussion, we assume that \((X, Y)\) is a random vector for our experiment, taking values in \(\R^2\).
The (joint) characteristic function \( \chi \) of \((X, Y)\) is defined by \[ \chi(s, t) = \E\left[\exp(i s X + i t Y)\right], \quad (s, t) \in \R^2 \]
Once again, the most important fact is that \(\chi\) completely determines the distribution: two random vectors taking values in \(\R^2\) have the same characteristic function if and only if they have the same distribution.
The joint moments can be obtained from the derivatives of the characteristic function.
Suppose that \( (X, Y) \) has characteristic function \( \chi \). If \(m, \, n \in \N\) and \(\E\left(\left|X^m Y^n\right|\right) \lt \infty\) then \[ \chi^{(m, n)}(0, 0) = e^{i \, (m + n)} \E\left(X^m Y^n\right) \]
The marginal characteristic functions and the characteristic function of the sum can be easily obtained from the joint characteristic function:
Suppose again that \( (X, Y) \) has characteristic function \( \chi \), and let \(\chi_1\), \(\chi_2\), and \(\chi_+\) denote the characteristic functions of \(X\), \(Y\), and \(X + Y\), respectively. For \(t \in \R\)
- \(\chi(t, 0) = \chi_1(t)\)
- \(\chi(0, t) = \chi_2(t)\)
- \(\chi(t, t) = \chi_+(t)\)
Proof
All three results follow immediately from the definitions.
Suppose again that \( \chi_1 \), \( \chi_2 \), and \( \chi \) are the characteristic functions of \(X\), \(Y\), and \( (X, Y) \) respectively. Then \( X \) and \( Y \) are independent if and only if \(\chi(s, t) = \chi_1(s) \chi_2(t)\) for all \((s, t) \in \R^2\).
Naturally, the results for bivariate characteristic functions have analogies in the general multivariate case. Only the notation is more complicated.
Examples and Applications
As always, be sure to try the computational problems yourself before expanding the solutions and answers in the text.
Dice
Recall that an ace-six flat die is a six-sided die for which faces numbered 1 and 6 have probability \( \frac{1}{4} \) each, while faces numbered 2, 3, 4, and 5 have probability \( \frac{1}{8} \) each. Similarly, a 3-4 flat die is a six-sided die for which faces numbered 3 and 4 have probability \( \frac{1}{4} \) each, while faces numbered 1, 2, 5, and 6 have probability \( \frac{1}{8} \) each.
Suppose that an ace-six flat die and a 3-4 flat die are rolled. Use probability generating functions to find the probability density function of the sum of the scores.
Solution
Let \( X \) and \( Y \) denote the score on the ace-six die and 3-4 flat die, respectively. Then \( X \) and \( Y \) have PGFs \( P \) and \( Q \) given by \begin{align*} P(t) &= \frac{1}{4} t + \frac{1}{8} t^2 + \frac{1}{8} t^3 + \frac{1}{8} t^4 + \frac{1}{8} t^5 + \frac{1}{4} t^6, \quad t \in \R\\ Q(t) &= \frac{1}{8} t + \frac{1}{8} t^2 + \frac{1}{4} t^3 + \frac{1}{4} t^4 + \frac{1}{8} t^5 + \frac{1}{8} t^6, \quad t \in \R \end{align*} Hence \( X + Y \) has PGF \( P Q \). Expanding (a computer algebra program helps) gives \[ P(t) Q(t) = \frac{1}{32} t^2 + \frac{3}{64} t^3 + \frac{3}{32} t^4 + \frac{1}{8} t^5 + \frac{1}{8} t^6 + \frac{5}{32} t^7 + \frac{1}{8} t^8 + \frac{1}{8} t^9 + \frac{3}{32} t^{10} + \frac{3}{64} t^{11} + \frac{1}{32} t^{12}, \quad t \in \R\] Thus the PDF \( f \) of \( X + Y \) is given by \( f(2) = f(12) = \frac{1}{32} \), \( f(3) = f(11) = \frac{3}{64} \), \( f(4) = f(10) = \frac{3}{32} \), \( f(5) = f(6) = f(8) = f(9) = \frac{1}{8} \) and \( f(7) = \frac{5}{32} \).
Two fair, 6-sided dice are rolled. One has faces numbered \( (0, 1, 2, 3, 4, 5) \) and the other has faces numbered \( (0, 6, 12, 18, 24, 30) \). Use probability generating functions to find the probability density function of the sum of the scores, and identify the distribution.
Solution
Let \( X \) and \( Y \) denote the score on the first die and the second die described, respectively. Then \( X \) and \( Y \) have PGFs \( P \) and \( Q \) given by \begin{align*} P(t) &= \frac{1}{6} \sum_{k=0}^5 t^k \quad t \in \R \\ Q(t) &= \frac{1}{6} \sum_{j=0}^5 t^{6 j} \quad t \in \R \end{align*} Hence \( X + Y \) has PGF \( P Q \). Simplifying gives \[ P(t) Q(t) = \frac{1}{36} \sum_{j=0}^5 \sum_{k=0}^5 t^{6 j + k} = \frac{1}{36} \sum_{n=0}^{35} t^n, \quad t \in \R\] Hence \( X + Y \) is uniformly distributed on \( \{0, 1, 2, \ldots, 35\} \).
Suppose that random variable \( Y \) has probability generating function \( P \) given by \[ P(t) = \left(\frac{2}{5} t + \frac{3}{10} t^2 + \frac{1}{5} t^3 + \frac{1}{10} t^4\right)^5, \quad t \in \R \]
- Interpret \( Y \) in terms of rolling dice.
- Use the probability generating function to find the first two factorial moments of \( Y \).
- Use (b) to find the variance of \( Y \).
Answer
- A four-sided die has faces numbered \((1, 2, 3, 4)\) with respective probabilities \( \left(\frac{2}{5}, \frac{3}{10}, \frac{1}{5}, \frac{1}{10}\right) \). \( Y \) is the sum of the scores when the die is rolled 5 times.
- \( \E(Y) = P^\prime(1) = 10 \), \( \E[Y(Y - 1)] = P^{\prime \prime}(1) = 95 \)
- \( \var(Y) = 5 \)
Bernoulli Trials
Suppose \(X\) is an indicator random variable with \(p = \P(X = 1)\), where \(p \in [0, 1]\) is a parameter. Then \(X\) has probability generating function \(P(t) = 1 - p + p t\) for \(t \in \R\).
Proof
\( P(t) = \E\left(t^X\right) = t^0 (1 - p) + t^1 p = 1 - p + p t \) for \( t \in \R \).
Recall that a Bernoulli trials process is a sequence \((X_1, X_2, \ldots)\) of independent, identically distributed indicator random variables. In the usual language of reliability, \(X_i\) denotes the outcome of trial \(i\), where 1 denotes success and 0 denotes failure. The probability of success \(p = \P(X_i = 1)\) is the basic parameter of the process. The process is named for Jacob Bernoulli. A separate chapter on the Bernoulli Trials explores this process in more detail.
For \(n \in \N_+\), the number of successes in the first \(n\) trials is \(Y_n = \sum_{i=1}^n X_i\). Recall that this random variable has the binomial distribution with parameters \(n\) and \(p\), which has probability density function \( f_n \) given by \[ f_n(y) = \binom{n}{y} p^y (1 - p)^{n - y}, \quad y \in \{0, 1, \ldots, n\} \]
Random variable \(Y_n\) has probability generating function \(P_n\) given by \(P_n(t) = (1 - p + p t)^n\) for \( t \in \R \).
Proof
This follows immediately from the PGF of an indicator variable and the result for sums of independent variables.
Rando variable \(Y_n\) has the following parameters:
- \(\E\left[Y_n^{(k)}\right] = n^{(k)} p^k\)
- \(\E\left(Y_n\right) = n p\)
- \(\var\left(Y_n\right) = n p (1 - p)\)
- \(\P(Y_n \text{ is even}) = \frac{1}{2}\left[1 - (1 - 2 p)^n\right]\)
Proof
- Repeated differentiation gives \( P^{(k)}(t) = n^{(k)} p^k (1 - p + p t)^{n-k} \). Hence \( P^{(k)}(1) = n^{(k)} p^k \), which is \( \E\left[X^{(k)} \right]\) by the moment result above.
- This follows from the formula for mean.
- This follows from the formula for variance.
- This follows from the even value formula.
Suppose that \(U\) has the binomial distribution with parameters \(m \in \N_+\) and \(p \in [0, 1]\), \(V\) has the binomial distribution with parameters \(n \in \N_+\) and \(q \in [0, 1]\), and that \(U\) and \(V\) are independent.
- If \(p = q\) then \(U + V\) has the binomial distribution with parameters \(m + n\) and \(p\).
- If \(p \ne q\) then \(U + V\) does not have a binomial distribution.
Proof
From the result for sums of independent variables and the PGF of the binomial distribution, note that the probability generating function of \(U + V\) is \(P(t) = (1 - p + p t)^m (1 - q + q t)^n\) for \(t \in \R\).
- If \( p = q \) then \( U + V \) has PGF \( P(t) = (1 - p + p t)^{m + n} \), which is the PGF of the binomial distribution with parameters \( m + n \) and \( p \).
- On the other hand, if \( p \ne q \), the PGF \( P \) does not have the functional form of a binomial PGF.
Suppose now that \( p \in (0, 1] \). The trial number \( N \) of the first success in the sequence of Bernoulli trials has the geometric distribution on \( \N_+ \) with success parameter \( p \). The probability density function \( h \) is given by \[h(n) = p (1 - p)^{n-1}, \quad n \in \N_+\] The geometric distribution is studied in more detail in the chapter on Bernoulli trials.
Let \(Q\) denote the probability generating function of \(N\). Then
- \(Q(t) = \frac{p t}{1 - (1 - p)t}\) for \(-\frac{1}{1 - p} \lt t \lt \frac{1}{1 - p}\)
- \(\E\left[N^{(k)}\right] = k! \frac{(1 - p)^{k-1}}{p^k}\) for \( k \in \N \)
- \(\E(N) = \frac{1}{p}\)
- \(\var(N) = \frac{1 - p}{p^2}\)
- \(\P(N \text{ is even}) = \frac{1 - p}{2 - p}\)
Proof
- Using the formula for the sum of a geometric series, \[ Q(t) = \sum_{n=1}^\infty (1 - p)^{n-1} p t^n = p t \sum_{n=1}^\infty [(1 - p) t]^{n-1} = \frac{p t}{1 - (1 - p) t}, \quad \left|(1 - p) t\right| \lt 1 \]
- Repeated differentiation gives \( H^{(k)}(t) = k! p (1 - p)^{k-1} \left[1 - (1 - p) t\right]^{-(k+1)} \) and then the result follows from the inversion formula.
- This follows from (b) and the formula for mean.
- This follows from (b) and the formula for variance.
- This follows from even value formula.
The probability that \( N \) is even comes up in the alternating coin tossing game with two players.
The Poisson Distribution
Recall that the Poisson distribution has probability density function \(f\) given by \[ f(n) = e^{-a} \frac{a^n}{n!}, \quad n \in \N \] where \(a \in (0, \infty)\) is a parameter. The Poisson distribution is named after Simeon Poisson and is widely used to model the number of random points
in a region of time or space; the parameter is proportional to the size of the region of time or space. The Poisson distribution is studied in more detail in the chapter on the Poisson Process.
Suppose that \(N\) has Poisson distribution with parameter \(a \in (0, \infty)\). Let \(P_a\) denote the probability generating function of \(N\). Then
- \(P_a(t) = e^{a (t - 1)}\) for \(t \in \R\)
- \(\E\left[N^{(k)}\right] = a^k\)
- \(\E(N) = a\)
- \(\var(N) = a\)
- \(\P(N \text{ is even}) = \frac{1}{2}\left(1 + e^{-2 a}\right)\)
Proof
- Using the exponential series, \[ P_a(t) = \sum_{n=0}^\infty e^{-a} \frac{a^n}{n!} t^n = e^{-a} \sum_{n=0}^\infty \frac{(a t)^n}{n!} = e^{-a} e^{a t}, \quad t \in \R \]
- Repeated differentiation gives \( P_a^{(k)}(t) = e^{a (t - 1)} a^k \), so the result follows from inversion formula.
- This follows from (b) and the formula for mean.
- This follows from (b) and the formula for variance.
- This follows from even value formula.
The Poisson family of distributions is closed with respect to sums of independent variables, a very important property.
Suppose that \(X, \, Y\) have Poisson distributions with parameters \(a, \, b \in (0, \infty)\), respectively, and that \(X\) and \(Y\) are independent. Then \(X + Y\) has the Poisson distribution with parameter \(a + b\).
Proof
In the notation of the previous result, note that \( P_a P_b = P_{a+b} \).
The right distribution function of the Poisson distribution does not have a simple, closed-form expression. The following exercise gives an upper bound.
Suppose that \(N\) has the Poisson distribution with parameter \(a \gt 0\). Then \[ \P(N \ge n) \le e^{n - a} \left(\frac{a}{n}\right)^n, \quad n \gt a \]
Proof
The PGF of \( N \) is \( P(t) = e^{a (t - 1)} \) and hence the MGF is \( P\left(e^t\right) = \exp\left(a e^t - a\right) \). From the Chernov bounds we have \[ \P(N \ge n) \le e^{-t n} \exp\left(a e^t - a\right) = \exp\left(a e^t - a - tn\right) \] If \( n \gt a \) the expression on the right is minimized when \( t = \ln(n / a) \). Substituting gives the upper bound.
The following theorem gives an important convergence result that is explored in more detail in the chapter on the Poisson process.
Suppose that \( p_n \in (0, 1) \) for \( n \in \N_+ \) and that \( n p_n \to a \in (0, \infty) \) as \( n \to \infty \). Then the binomial distribution with parameters \( n \) and \( p_n \) converges to the Poisson distribution with parameter \( a \) as \( n \to \infty \).
Proof
Let \(P_n\) denote the probability generating function of the binomial distribution with parameters \(n\) and \(p_n\). From the PGF of the binomial distribution we have \[ P_n(t) = \left[1 + p_n (t - 1)\right]^n = \left[1 + \frac{n p_n (t - 1)}{n}\right]^n, \quad t \in \R\] Using a famous theorem from calculus, \( P_n(t) \to e^{a (t - 1)} \) as \( n \to \infty \). But this is the PGF of the Poisson distribution with parameter \( a \), so the result follows from the continuity theorem for PGFs.
The Exponential Distribution
Recall that the exponential distribution is a continuous distribution on \([0, \infty)\) with probability density function \(f\) given by \[ f(t) = r e^{-r t}, \quad t \in (0, \infty) \] where \(r \in (0, \infty)\) is the rate parameter. This distribution is widely used to model failure times and other random times, and in particular governs the time between arrivals in the Poisson model. The exponential distribution is studied in more detail in the chapter on the Poisson Process.
Suppose that \(T\) has the exponential distribution with rate parameter \(r \in (0, \infty)\) and let \(M\) denote the moment generating function of \(T\). Then
- \(M(s) = \frac{r}{r - s}\) for \(s \in (-\infty, r)\).
- \(\E(T^n) = n! / r^n\) for \(n \in \N\)
Proof
- \( M(s) = \E\left(e^{s T}\right) = \int_0^\infty e^{s t} r e^{-r t} \, dt = \int_0^\infty r e^{(s - r) t} \, dt = \frac{r}{r - s} \) for \( s \lt r \).
- \( M^{(n)}(s) = \frac{r n!}{(r - s)^{n+1}} \) for \( n \in \N \)
Suppose that \((T_1, T_2, \ldots)\) is a sequence of independent random variables, each having the exponential distribution with rate parameter \(r \in (0, \infty)\). For \(n \in \N_+\), the moment generating function \( M_n \) of \(U_n = \sum_{i=1}^n T_i\) is given by \[ M_n(s) = \left(\frac{r}{r - s}\right)^n, \quad s \in (-\infty, r) \]
Proof
This follows from the previous result and the result for sums of independent variables.
Random variable \(U_n\) has the Erlang distribution with shape parameter \(n\) and rate parameter \(r\), named for Agner Erlang. This distribution governs the \( n \)th arrival time in the Poisson model. The Erlang distribution is a special case of the gamma distribution and is studied in more detail in the chapter on the Poisson Process.
Uniform Distributions
Suppose that \( a, \, b \in \R \) and \( a \lt b \). Recall that the continuous uniform distribution on the interval \( [a, b] \) has probability density function \( f \) given by \[ f(x) = \frac{1}{b - a}, \quad x \in [a, b] \] The distribution corresponds to selecting a point at random from the interval. Continuous uniform distributions arise in geometric probability and a variety of other applied problems.
Suppose that \(X\) is uniformly distributed on the interval \([a, b]\) and let \(M\) denote the moment generating function of \(X\). Then
- \(M(t) = \frac{e^{b t} - e^{a t}}{(b - a)t}\) if \( t \ne 0 \) and \( M(0) = 1 \)
- \(\E\left(X^n\right) = \frac{b^{n+1} - a^{n + 1}}{(n + 1)(b - a)}\) for \(n \in \N\)
Proof
- \( M(t) = \int_a^b e^{t x} \frac{1}{b - a} \, dx = \frac{e^{b t} - e^{a t}}{(b - a)t}\) if \( t \ne 0 \). Trivially \( M(0) = 1 \)
- This is a case where the MGF is not helpful, and it's much easier to compute the moments directly: \( \E\left(X^n\right) = \int_a^b x^n \frac{1}{b - a} \, dx = \frac{b^{n+1} - a^{n + 1}}{(n + 1)(b - a)} \)
Suppose that \((X, Y)\) is uniformly distributed on the triangle \(T = \{(x, y) \in \R^2: 0 \le x \le y \le 1\}\). Compute each of the following:
- The joint moment generating function of \((X, Y)\).
- The moment generating function of \(X\).
- The moment generating function of \(Y\).
- The moment generating function of \(X + Y\).
Answer
- \(M(s, t) = 2 \frac{e^{s+t} - 1}{s (s + t)} - 2 \frac{e^t - 1}{s t}\) if \( s \ne 0, \; t \ne 0\). \( M(0, 0) = 1 \)
- \(M_1(s) = 2 \left(\frac{e^2}{s^2} - \frac{1}{s^2} - \frac{1}{s}\right)\) if \(s \ne 0\). \( M_1(0) = 1 \)
- \(M_2(t) = 2 \frac{t e^t - e^t + 1}{t^2}\) if \( t \ne 0\). \( M_2(0) = 1 \)
- \(M_+(t) = \frac{e^{2 t} - 1}{t^2} - 2 \frac{e^t - 1}{t^2}\) if \(t \ne 0\). \( M_+(0) = 1 \)
A Bivariate Distribution
Suppose that \( (X, Y) \) has probability density function \(f\) given by \(f(x, y) = x + y\) for \((x, y) \in [0, 1]^2\). Compute each of the following:
- The joint moment generating function \( (X, Y) \).
- The moment generating function of \(X\).
- The moment generating function of \(Y\).
- The moment generating function of \(X + Y\).
Answer
- \(M(s, t) = \frac{e^{s+t}(-2 s t + s + t) + e^s(s t - s - t) + s + t}{s^2 t^2}\) if \(s \ne 0, \, t \ne 0\). \( M(0, 0) = 1 \)
- \(M_1(s) = \frac{3 s e^2 - 2 e^2 - s + 2}{2 s^2}\) if \(s \ne 0\). \( M_1(0) = 1 \)
- \(M_2(t) = \frac{3 t e^t - 2 e^t - t + 2}{2 t^2}\) if \(t \ne 0\). \( M_2(0) = 1 \)
- \(M_+(t) = \frac{[e^{2 t}(1 - t) + e^t (t - 2) + 1]}{t^3}\) if \(t \ne 0\). \( M_+(0) = 1 \)
The Normal Distribution
Recall that the standard normal distribution is a continuous distribution on \(\R) with probability density function \(\phi\) given by \[ \phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} z^2}, \quad z \in \R \] Normal distributions are widely used to model physical measurements subject to small, random errors and are studied in more detail in the chapter on Special Distributions.
Suppose that \(Z\) has the standard normal distribution and let \(M\) denote the moment generating function of \(Z\). Then
- \(M(t) = e^{\frac{1}{2} t^2}\) for \(t \in \R\)
- \(\E\left(Z^n\right) = 1 \cdot 3 \cdots (n - 1)\) if \( n \) is even and \(\E\left(Z^n\right) = 0\) if \(n\) is odd.
Proof
- First, \[ M(t) = \E\left(e^{t Z}\right) = \int_{-\infty}^\infty e^{t z} \frac{1}{\sqrt{2 \pi}} e^{-z^2 / 2} \, dz = \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp\left(-\frac{z^2}{2} + t z\right) \, dz \] Completing the square in \( z \) gives \(\exp\left(-\frac{z^2}{2} + t z\right) = \exp\left[\frac{1}{2} t^2 - \frac{1}{2}(z - t)^2 \right] = e^{\frac{1}{2} t^2} \exp\left[-\frac{1}{2} (z - t)^2\right] \). hence \[ M(t) = e^{\frac{1}{2} t^2} \int_{-\infty}^\infty \frac{1}{\sqrt{2 \pi}} \exp\left[-\frac{1}{2} (z - t)^2\right] \, dz = e^{\frac{1}{2} t^2} \] because the function of \( z \) in the last integral is the probability density function for the normal distribution with mean \( t \) and variance 1.
- Note that \( M^\prime(t) = t M(t) \). Thus, repeated differentiation gives \( M^{(n)}(t) = p_n(t) M(t) \) for \( n \in \N \), where \( p_n \) is a polynomial of degree \( n \) satisfying \( p_{n+1}^\prime(t) = t p_n(t) + p_n^\prime(t) \). Since \( p_0 = 1 \), it's easy to see that \( p_n \) has only even or only odd terms, depending on whether \( n \) is even or odd, respectively. Thus, \( \E\left(X^n\right) = p_n(0) \). This is 0 if \( n \) is odd, and is the constant term \( 1 \cdot 3 \cdots (n - 1) \) if \( n \) is even. Of course, we can also see that the odd order moments must be 0 by symmetry.
More generally, for \(\mu \in \R\) and \(\sigma \in (0, \infty)\), recall that the normal distribution with mean \(\mu\) and standard deviation \(\sigma\) is a continuous distribution on \(\R\) with probability density function \( f \) given by \[ f(x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp\left[-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2\right], \quad x \in \R \] Moreover, if \( Z \) has the standard normal distribution, then \( X = \mu + \sigma Z \) has the normal distribution with mean \( \mu \) and standard deviation \( \sigma \). Thus, we can easily find the moment generating function of \( X \):
Suppose that \(X\) has the normal distribution with mean \(\mu\) and standard deviation \(\sigma\). The moment generating function of \(X\) is \[M(t) = \exp\left(\mu t + \frac{1}{2} \sigma^2 t^2\right), \quad t \in \R\]
Proof
This follows easily the previous result and the result for linear transformations: \( X = \mu + \sigma Z \) where \( Z \) has the standard normal distribution. Hence \[ M(t) = \E\left(e^{t X}\right) = e^{\mu t} \E\left(e^{\sigma t Z}\right) = e^{\mu t} e^{\frac{1}{2} \sigma^2 t ^2}, \quad t \in \R \]
So the normal family of distributions in closed under location-scale transformations. The family is also closed with respect to sums of independent variables:
If \(X\) and \(Y\) are independent, normally distributed random variables then \(X + Y\) has a normal distribution.
Proof
Suppose that \( X \) has the normal distribution with mean \( \mu \in \R \) and standard deviation \( \sigma \in (0, \infty) \), and that \( Y \) has the normal distribution with mean \( \nu \in \R \) and standard deviation \( \tau \in (0, \infty) \). By (14), the MGF of \( X + Y \) is \[ M_{X+Y}(t) = M_X(t) M_Y(t) = \exp\left(\mu t + \frac{1}{2} \sigma^2 t^2\right) \exp\left(\nu t + \frac{1}{2} \tau^2 t^2\right) = \exp\left[(\mu + \nu) t + \frac{1}{2}\left(\sigma^2 + \tau^2\right) t^2 \right] \] which we recognize as the MGF of the normal distribution with mean \( \mu + \nu \) and variance \( \sigma^2 + \tau^2 \). Of course, we already knew that \( \E(X + Y) = \E(X) + \E(Y) \), and since \( X \) and \( Y \) are independent, \( \var(X + Y) = \var(X) + \var(Y) \), so the new information is that the distribution is also normal.
The Pareto Distribution
Recall that the Pareto distribution is a continuous distribution on \([1, \infty) with probability density function \(f\) given by \[ f(x) = \frac{a}{x^{a + 1}}, \quad x \in [1, \infty) \] where \(a \in (0, \infty)\) is the shape parameter. The Pareto distribution is named for Vilfredo Pareto. It is a heavy-tailed distribution that is widely used to model financial variables such as income. The Pareto distribution is studied in more detail in the chapter on Special Distributions.
Suppose that \(X\) has the Pareto distribution with shape parameter \( a \), and let \( M \) denote the moment generating function of \( X \). Then
- \(\E\left(X^n\right) = \frac{a}{a - n}\) if \(n \lt a\) and \(\E\left(X^n\right) = \infty\) if \(n \ge a\)
- \(M(t) = \infty\) for \(t \gt 0\)
Proof
- We have seen this computation before. \( \E\left(X^n\right) = \int_1^\infty x^n \frac{a}{x^{a+1}} \, dx = \int_1^\infty x^{n - a - 1} \, dx \). The integral evaluates to \( \frac{a}{a - n} \) if \( n \lt a \) and \( \infty \) if \( n \ge a \).
- This follows from part (a). Since \( X \ge 1 \), \( M(t) \) is increasing in \( t \). Thus \( M(t) \le 1 \) if \( t \lt 0 \). If \( M(t) \lt \infty \) for some \( t \gt 0 \), then \( M(t) \) would be finite for \( t \) in an open interval about 0, in which case \( X \) would have finite moments of all orders. Of course, it's also easy to see directly from the integral that \( M(t) = \infty \) for \( t \gt 0 \)
On the other hand, like all distributions on \( \R \), the Pareto distribution has a characteristic function. However, the characteristic function of the Pareto distribution does not have a simple, closed form.
The Cauchy Distribution
Recall that the (standard) Cauchy distribution is a continuous distribution on \(\R\) with probability density function \(f\) given by \[ f(x) = \frac{1}{\pi \left(1 + x^2\right)}, \quad x \in \R \] and is named for Augustin Cauchy. The Cauch distribution is studied in more generality in the chapter on Special Distributions. The graph of \(f\) is known as the Witch of Agnesi, named for Maria Agnesi.
Suppose that \( X \) has the standard Cauchy distribution, and let \(M\) denote the moment generating function of \(X\). Then
- \(\E(X)\) does not exist.
- \(M(t) = \infty\) for \(t \ne 0\).
Proof
- We have seen this computation before. \( \int_a^\infty \frac{x}{\pi (1 + x^2)} \, dx = \infty \) and \( \int_{-\infty}^a \frac{x}{\pi (1 + x^2)} \, dx = -\infty \) for every \( a \in \R \), so \( \int_{-\infty}^\infty \frac{x}{\pi (1 + x^2)} \, dx \) does not exist.
- Note that \( \int_0^\infty \frac{e^{t x}}{\pi (1 + x^2) } \, dx = \infty\) if \( t \ge 0 \) and \( \int_{-\infty}^0 \frac{e^{t x}}{\pi (1 + x^2)} \, dx = \infty \) if \( t \le 0 \).
Once again, all distributions on \( \R \) have characteristic functions, and the standard Cauchy distribution has a particularly simple one.
Let \(\chi\) denote the characteristic function of \(X\). Then \(\chi(t) = e^{-\left|t\right|}\) for \(t \in \R\).
Proof
The proof of this result requires contour integrals in the complex plane, and is given in the section on the Cauchy distribution in the chapter on special distributions.
Counterexample
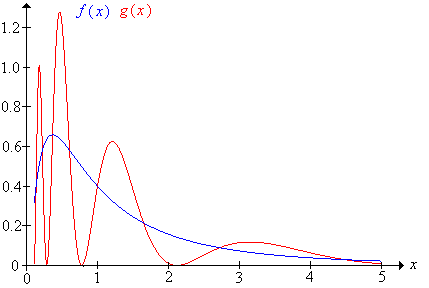
For the Pareto distribution, only some of the moments are finite; so course, the moment generating function cannot be finite in an interval about 0. We will now give an example of a distribution for which all of the moments are finite, yet still the moment generating function is not finite in any interval about 0. Furthermore, we will see two different distributions that have the same moments of all orders.
Suppose that Z has the standard normal distribution and let \(X = e^Z\). The distribution of \(X\) is known as the (standard) lognormal distribution. The lognormal distribution is studied in more generality in the chapter on Special Distributions. This distribution has finite moments of all orders, but infinite moment generating function.
\(X\) has probability density function \(f\) given by \[ f(x) = \frac{1}{\sqrt{2 \pi} x} \exp\left(-\frac{1}{2} \ln^2(x)\right), \quad x \gt 0 \]
- \(\E\left(X^n\right) = e^{\frac{1}{2}n^2}\) for \(n \in \N\).
- \(\E\left(e^{t X}\right) = \infty\) for \(t \gt 0\).
Proof
We use the change of variables theorem. The transformation is \( x = e^z \) so the inverse transformation is \( z = \ln x \) for \( x \in (0, \infty) \) and \( z \in \R \). Letting \( \phi \) denote the PDF of \( Z \), it follows that the PDF of \( X \) is \( f(x) = \phi(z) \, dz / dx = \phi\left(\ln x\right) \big/ x \) for \( x \gt 0 \).
- We use the moment generating function of the standard normal distribution given above: \( \E\left(X^n\right) = \E\left(e^{n Z}\right) = e^{n^2 / 2}\).
- Note that \[ \E\left(e^{t X}\right) = \E\left[\sum_{n=0}^\infty \frac{(t X)^n}{n!}\right] = \sum_{n=0}^\infty \frac{\E(X^n)}{n!} t^n = \sum_{n=0}^\infty \frac{e^{n^2 / 2}}{n!} t^n = \infty, \quad t \gt 0 \] The interchange of expected value and sum is justified since \( X \) is nonnegative. See the advanced section on properties of the integral in the chapter on Distributions for more details.
Next we construct a different distribution with the same moments as \( X \).
Let \(h\) be the function defined by \(h(x) = \sin\left(2 \pi \ln x \right)\) for \(x \gt 0\) and let \(g\) be the function defined by \(g(x) = f(x)\left[1 + h(x)\right]\) for \(x \gt 0\). Then
- \(g\) is a probability density function.
- If \( Y \) has probability density function \( g \) then \(\E\left(Y^n\right) = e^{\frac{1}{2} n^2}\) for \(n \in \N\)
Proof