1.5: Equivalence Relations
- Page ID
- 10120
Basic Theory
A relation \(\approx\) on a nonempty set \(S\) that is reflexive, symmetric, and transitive is an equivalence relation on \(S\). Thus, for all \( x, \, y, \, z \in S \),
- \( x \approx x \), the reflexive property.
- If \( x \approx y \) then \( y \approx x \), the symmetric property.
- If \( x \approx y \) and \( y \approx z \) then \( x \approx z \), the transitive property.
As the name and notation suggest, an equivalence relation is intended to define a type of equivalence among the elements of \(S\). Like partial orders, equivalence relations occur naturally in most areas of mathematics, including probability.
Suppose that \( \approx \) is an equivalence relation on \( S \). The equivalence class of an element \(x \in S\) is the set of all elements that are equivalent to \(x\), and is denoted \[ [x] = \{y \in S: y \approx x\} \]
Results
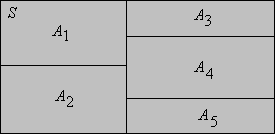
The most important result is that an equivalence relation on a set \(S\) defines a partition of \(S\), by means of the equivalence classes.
Suppose that \(\approx\) is an equivalence relation on a set \(S\).
- If \(x \approx y\) then \([x] = [y]\).
- If \(x \not \approx y\) then \([x] \cap [y] = \emptyset\).
- The collection of (distinct) equivalence classes is a partition of \( S \) into nonempty sets.
Proof
- Suppose that \( x \approx y \). If \( u \in [x] \) then \( u \approx x \) and hence \( u \approx y \) by the transitive property. Hence \( u \in [y] \). Similarly, if \( u \in [y] \) then \( u \approx y \). But \( y \approx x \) by the symmetric property, and hence \( u \approx x \) by the transitive property. Hence \( u \in [x] \).
- Suppose that \( x \not \approx y \). If \( u \in [x] \cap [y] \), then \( u \in [x] \) and \( u \in [y] \), so \( u \approx x \) and \( u \approx y \). But then \( x \approx u \) by the symmetric property, and then \( x \approx y \) by the transitive property. This is a contradiction, so \( [x] \cap [y] = \emptyset \).
- From (a) and (b), the (distinct) equivalence classes are disjoint. If \( x \in S \), then \( x \approx x \) by the reflexive property, and hence \( x \in [x] \). Therefore \( \bigcup_{x \in S} [x] = S \).
Sometimes the set \(\mathscr{S}\) of equivalence classes is denoted \(S / \approx\). The idea is that the equivalence classes are new objects
obtained by identifying
elements in \(S\) that are equivalent. Conversely, every partition of a set defines an equivalence relation on the set.
Suppose that \(\mathscr{S}\) is a collection of nonempty sets that partition a given set \(S\). Define the relation \( \approx \) on \( S \) by \( x \approx y \) if and only if \( x \in A \) and \( y \in A \) for some \( A \in \mathscr{S} \).
- \( \approx \) is an equivalence relation.
- \( \mathscr{S} \) is the set of equivalence classes.
Proof
- If \( x \in S \), then \( x \in A \) for some \( A \in \mathscr{S} \), since \( \mathscr{S} \) partitions \( S \). Hence \( x \approx x \), and so the reflexive property holds. Next, \( \approx \) is trivially symmetric by definition. Finally, suppose that \( x \approx y \) and \( y \approx z \). Then \( x, \, y \in A \) for some \( A \in \mathscr{S} \) and \( y, \, z \in B \) for some \( B \in \mathscr{S} \). But then \( y \in A \cap B \). The sets in \( \mathscr{S} \) are disjoint, so \( A = B \). Hence \( x, \, z \in A \), so \( x \approx z \). Thus \( \approx \) is transitive.
- If \( x \in S \), then \( x \in A \) for a unique \( A \in \mathscr{S} \), and then by definition, \( [x] = A \).
Sometimes the equivalence relation \(\approx\) associated with a given partition \(\mathscr{S}\) is denoted \(S / \mathscr{S}\). The idea, of course, is that elements in the same set of the partition are equivalent.
The process of forming a partition from an equivalence relation, and the process of forming an equivalence relation from a partition are inverses of each other.
- If we start with an equivalence relation \(\approx\) on \(S\), form the associated partition, and then construct the equivalence relation associated with the partition, then we end up with the original equivalence relation. In modular notation, \(S \big/ (S / \approx)\) is the same as \(\approx\).
- If we start with a partition \(\mathscr{S}\) of \(S\), form the associated equivalence relation, and then form the partition associated with the equivalence relation, then we end up with the original partition. In modular notation, \(S \big/ (S / \mathscr{S})\) is the same as \(\mathscr{S}\).
Suppose that \( S \) is a nonempty set. The most basic equivalence relation on \( S \) is the equality relation \( = \). In this case \( [x] = \{x\} \) for each \( x \in S \). At the other extreme is the trivial relation \( \approx \) defined by \( x \approx y \) for all \( x, \, y \in S \). In this case \( S \) is the only equivalence class.
Every function \(f\) defines an equivalence relation on its domain, known as the equivalence relation associated with \(f\). Moreover, the equivalence classes have a simple description in terms of the inverse images of \(f\).
Suppose that \(f: S \to T\). Define the relation \(\approx\) on \(S\) by \(x \approx y\) if and only if \(f(x) = f(y)\).
- The relation \(\approx\) is an equivalence relation on \(S\).
- The set of equivalences classes is \(\mathscr{S} = \left\{f^{-1}\{t\}: t \in \range(f)\right\}\).
- The function \(F: \mathscr{S} \to T\) defined by \(F([x]) = f(x)\) is well defined and is one-to-one.
Proof
- If \( x \in S \) then trivially \( f(x) = f(x) \), so \( x \approx x \). Hence \( \approx \) is reflexive. If \( x \approx y \) then \( f(x) = f(y) \) so trivially \( f(y) = f(x) \) and hence \( y \approx x \). Thus \( \approx \) is symmetric. If \( x \approx y \) and \( y \approx z \) then \( f(x) = f(y) \) and \( f(y) = f(z) \), so trivially \( f(x) = f(z) \) and so \( x \approx z \). Hence \( \approx \) is transitive.
- Recall that \( t \in \range(f) \) if and only if \( f(x) = t \) for some \( x \in S \). Then by definition, \( [x] = f^{-1}\{t\} = \{y \in S: f(y) = t\} = \{ y \in S: f(y) = f(x)\} \)
- From (3), \( [x] = [y] \) if and only if \( x \approx y \) if and only if \( f(x) = f(y) \). This shows both that \( F \) is well defined, and that \( F \) is one-to-one.
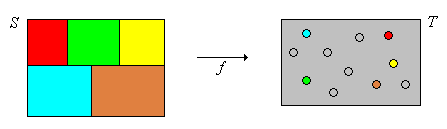
Suppose again that \(f: S \to T\).
- If \(f\) is one-to-one then the equivalence relation associated with \(f\) is the equality relation, and hence \([x] = \{x\}\) for each \(x \in S\).
- If \(f\) is a constant function then the equivalence relation associated with \(f\) is the trivial relation, and hence \(S\) is the only equivalence class.
Proof
- If \( f \) is one-to-one, then \( x \approx y \) if and only if \( f(x) = f(y) \) if and only if \( x = y \).
- If \( f \) is constant on \( S \) then \( f(x) = f(y) \) and hence \( x \approx y \) for all \( x, \, y \in S \).
Equivalence relations associated with functions are universal: every equivalence relation is of this form:
Suppose that \(\approx\) is an equivalence relation on a set \(S\). Define \(f: S \to \mathscr{P}(S)\) by \(f(x) = [x]\). Then \(\approx\) is the equivalence relation associated with \(f\).
Proof
From (6), \( x \approx y \) if and only if \( [x] = [y] \) if and only if \( f(x) = f(y) \).
The intersection of two equivalence relations is another equivalence relation.
Suppose that \(\approx\) and \(\cong\) are equivalence relations on a set \(S\). Let \(\equiv\) denote the intersection of \(\approx\) and \(\cong\) (thought of as subsets of \(S \times S\)). Equivalently, \(x \equiv y\) if and only if \(x \approx y\) and \(x \cong y\).
- \(\equiv\) is an equivalence relation on \(S\).
- \([x]_\equiv = [x]_\approx \cap [x]_\cong\).
Suppose that we have a relation that is reflexive and transitive, but fails to be a partial order because it's not anti-symmetric. The relation and its inverse naturally lead to an equivalence relation, and then in turn, the original relation defines a true partial order on the equivalence classes. This is a common construction, and the details are given in the next theorem.
Suppose that \(\preceq\) is a relation on a set \(S\) that is reflexive and transitive. Define the relation \(\approx\) on \(S\) by \(x \approx y\) if and only if \(x \preceq y\) and \(y \preceq x\).
- \(\approx\) is an equivalence relation on \(S\).
- If \(A\) and \(B\) are equivalence classes and \(x \preceq y\) for some \(x \in A\) and \(y \in B\), then \(u \preceq v\) for all \(u \in A\) and \(v \in B\).
- Define the relation \(\preceq\) on the collection of equivalence classes \(\mathscr{S}\) by \(A \preceq B\) if and only if \(x \preceq y\) for some (and hence all) \(x \in A\) and \(y \in B\). Then \(\preceq\) is a partial order on \(\mathscr{S}\).
Proof
- If \( x \in S \) then \( x \preceq x \) since \( \preceq \) is reflexive. Hence \( x \approx x \), so \( \approx \) is reflexive. Clearly \( \approx \) is symmetric by the symmetry of the definition. Suppose that \( x \approx y \) and \( y \approx z \). Then \( x \preceq y \), \( y \preceq z \), \( z \preceq y \) and \( y \preceq x \). Hence \( x \preceq z \) and \( z \preceq x \) since \( \preceq \) is transitive. Therefore \( x \approx z \) so \( \approx \) is transitive.
- Suppose that \( A \) and \( B \) are equivalence classes of \( \approx \) and that \( x \preceq y \) for some \( x \in A \) and \( y \in B \). If \( u \in A \) and \( v \in B \), then \( x \approx u \) and \( y \approx v \). Therefore \( u \preceq x \) and \( y \preceq v \). By transitivity, \( u \preceq v \).
- Suppose that \( A \in \mathscr{S} \). If \( x, \, y \in A \) then \( x \approx y \) and hence \( x \preceq y \). Therefore \( A \preceq A \) and so \( \preceq \) is reflexive. Next suppose that \( A, \, B \in \mathscr{S} \) and that \( A \preceq B \) and \( B \preceq A \). If \( x \in A \) and \( y \in B \) then \( x \preceq y \) and \( y \preceq x \). Hence \( x \approx y \) so \( A = B \). Therefore \( \preceq \) is antisymmetric. Finally, suppose that \( A, \, B, \, C \in \mathscr{S} \) and that \( A \preceq B \) and \( B \preceq C \). Note that \( B \ne \emptyset \) so let \( y \in B \). If \( x \in A, \, z \in C \) then \( x \preceq y \) and \( y \preceq z \). Hence \( x \preceq z \) and therefore \( A \preceq C \). So \( \preceq \) is transitive.
A prime example of the construction in the previous theorem occurs when we have a function whose range space is partially ordered. We can construct a partial order on the equivalence classes in the domain that are associated with the function.
Suppose that \(S\) and \(T\) are sets and that \(\preceq_T\) is a partial order on \(T\). Suppose also that \(f: S \to T\). Define the relation \(\preceq_S\) on \(S\) by \(x \preceq_S y\) if and only if \(f(x) \preceq_T f(y)\).
- \(\preceq_S\) is reflexive and transitive.
- The equivalence relation on \(S\) constructed in (10) is the equivalence relation associated with \(f\), as in (6).
- \(\preceq_S\) can be extended to a partial order on the equivalence classes corresponding to \(f\).
Proof
- If \( x \in S \) then \( f(x) \preceq_T f(x) \) since \( \preceq_T \) is reflexive, and hence \( x \preceq_S x \). Thus \( \preceq_S \) is reflexive. Suppose that \( x, \, y, \, z \in S \) and that \(x \preceq_S y \) and \( y \preceq_S z \). Then \( f(x) \preceq_T f(y) \) and \( f(y) \preceq_T f(z) \). Hence \( f(x) \preceq_T f(z) \) since \( \preceq_T \) is transitive. Thus \( \preceq_S \) is transitive.
- For the equivalence relation \( \approx \) on \( S \) constructed in (10), \( x \approx y \) if and only if \( x \preceq_S y \) and \( y \preceq_S x \) if and only if \( f(x) \preceq_T f(y) \) and \( f(y) \preceq_T f(x) \) if and only if \( f(x) = f(y) \), since \( \preceq_T \) is antisymmetric. Thus \( \approx \) is the equivalence relation associated with \( f \).
- This follows immediately from (10) and parts (a) and (b). If \( u, \, v \in \range(f) \), then \( f^{-1}(\{u\}) \preceq_S f^{-1}(\{v\}) \) if and only if \( u \preceq_T v \).
Examples and Applications
Simple functions
Give the equivalence classes explicitly for the functions from \(\R\) into \(\R\) defined below:
- \(f(x) = x^2\).
- \(g(x) = \lfloor x \rfloor\).
- \(h(x) = \sin(x)\).
Answer
- \([x] = \{x, -x\}\)
- \([x] = \left[ \lfloor x \rfloor, \lfloor x \rfloor + 1 \right)\)
- \([x] = \{x + 2 n \pi: n \in \Z\} \cup \{(2 n + 1) \pi - x: n \in \Z\}\)
Calculus
Suppose that \(I\) is a fixed interval of \(\R\), and that \(S\) is the set of differentiable functions from \(I\) into \(\R\). Consider the equivalence relation associated with the derivative operator \(D\) on \(S\), so that \(D(f) = f^{\prime}\). For \(f \in S\), give a simple description of \([f]\).
Answer
\([f] = \{f + c: c \in \R\}\)
Congruence
Recall the division relation \( \mid \) from \( \N_+\) to \( \Z \): For \( d \in \N_+ \) and \( n \in \Z \), \( d \mid n \) means that \( n = k d \) for some \( k \in \Z \). In words, \( d \) divides \( n \) or equivalently \( n \) is a multiple of \( d \). In the previous section, we showed that \( \mid \) is a partial order on \( \N_+ \).
Fix \( d \in \N_+ \).
- Define the relation \(\equiv_d\) on \(\Z\) by \(m \equiv_d n\) if and only if \(d \mid (n - m)\). The relation \(\equiv_d\) is known as congruence modulo \(d\).
- Let \(r_d: \Z \to \{0, 1, \ldots, d - 1\}\) be defined so that \(r(n)\) is the remainder when \(n\) is divided by \(d\).
Recall that by the Euclidean division theorem, named for Euclid of course, \( n \in \Z \) can be written uniquely in the form \( n = k d + q \) where \( k \in \Z \) and \( q \in \{0, 1, \ldots, d - 1\} \), and then \( r_d(n) = q \).
Congruence modulo \( d \).
- \( \equiv_d \) is the equivalence relation associated with the function \( r_d \).
- There are \( d \) distinct equivalence classes, given by \( [q]_d = \{q + k d: k \in \Z\}\) for \( q \in \{0, 1, \ldots, d - 1\} \).
Proof
- Recall that for the equivalence relation associated with \( r_d \), integers \( m \) and \( n \) are equivalent if and only if \( r_d(m) = r_d(n) \). By the division theorem, \( m = j d + p \) and \( n = k d + q \), where \( j, \, k \in \Z \) and \( p, \, q \in \{0. 1, \ldots, d - 1\} \), and these representations are unique. Thus \( n - m = (k - j) d + (q - p) \), and so \( m \equiv_d n \) if and only if \( d \mid (n - m) \) if and only if \( p = q \) if and only if \( r_d(m) = r_d(n) \).
- Recall that the equivalence classes are \( r_d^{-1}\{q\} \) for \( q \in \range\left(r_d\right) = \{0, 1, \ldots, d - 1\} \). By the division theorem, \( r_d^{-1}\{q\} = \{k d + q: k \in \Z\}\).
Explicitly give the equivalence classes for \( \equiv_4 \), congruence mod 4.
Answer
- \( [0]_4 = \{0, 4, 8, 12, \ldots\} \cup \{-4, -8, -12, -16, \ldots\} \)
- \( [1]_4 = \{1, 5, 9, 13, \ldots\} \cup \{-3, -7, -11, -15, \ldots\} \)
- \( [2]_4 = \{2, 6, 10, 14, \ldots\} \cup \{-2, -6, -10, -14, \ldots\} \)
- \( [3]_4 = \{3, 7, 11, 15, \ldots\} \cup \{-1, -5, -9, -13, \ldots\} \)
Linear Algebra
Linear algebra provides several examples of important and interesting equivalence relations. To set the stage, let \(\R^{m \times n}\) denote the set of \(m \times n\) matrices with real entries, for \( m, \, n \in \N_+ \).
Recall that the following are row operations on a matrix:
- Multiply a row by a non-zero real number.
- Interchange two rows.
- Add a multiple of a row to another row.
Row operations are essential for inverting matrices and solving systems of linear equations.
Matrices \(A, \, B \in \R^{m \times n}\) are row equivalent if \(A\) can be transformed into \(B\) by a finite sequence of row operations. Row equivalence is an equivalence relation on \(\R^{m \times n}\).
Proof.
If \( A \in \R^{m \times n} \), then \( A \) is row equivalent to itself: we can simply do nothing, or if you prefer, we can multiply the first row of \( A \) by 1. For symmetry, the key is that each row operation can be reversed by another row operation: multiplying a row by \( c \ne 0 \) is reversed by multiplying the same row of the resulting matrix by \( 1 / c \). Interchanging two rows is reversed by interchanging the same two rows of the resulting matrix. Adding \( c \) times row \( i \) to row \( j \) is reversed by adding \( -c \) times row \( i \) to row \( j \) in the resulting matrix. Thus, if we can transform \( A \) into \( B \) by a finite sequence of row operations, then we can transform \( B \) into \( A \) by applying the reversed row operations in the reverse order. Transitivity is clear: If we can transform \( A \) into \( B \) by a sequence of row operations and \( B \) into \( C \) by another sequence of row operations, then we can transform \( A \) into \( C \) by putting the two sequences together.
Our next relation involves similarity, which is very important in the study of linear transformations, change of basis, and the theory of eigenvalues and eigenvectors.
Matrices \(A, \, B \in \R^{n \times n}\) are similar if there exists an invertible \(P \in \R^{n \times n}\) such that \(P^{-1} A P = B\). Similarity is an equivalence relation on \(\R^{n \times n}\).
Proof
If \( A \in \R^{n \times n} \) then \( A = I^{-1} A I \), where \( I \) is the \( n \times n \) identity matrix, so \( A \) is similar to itself. Suppose that \( A, \, B \in \R^{n \times n} \) and that \( A \) is similar to \( B \) so that \( B = P^{-1} A P\) for some invertible \( P \in \R^{n \times n} \). Then \( A = P B P^{-1} = \left(P^{-1}\right)^{-1} B P^{-1} \) so \( B \) is similar to \( A \). Finally, suppose that \( A, \, B, \, C \in R^{n \times n} \) and that \( A \) is similar to \( B \) and that \( B \) is similar to \( C \). Then \( B = P^{-1} A P \) and \( C = Q^{-1} B Q \) for some invertible \( P, \, Q \in R^{n \times n} \). Then \( C = Q^{-1} P^{-1} A P Q = (P Q)^{-1} A (P Q) \), so \( A \) is similar to \( C \).
Next recall that for \( A \in \R^{m \times n} \), the transpose of \( A \) is the matrix \( A^T \in \R^{n \times m} \) with the property that \( (i, j) \) entry of \( A \) is the \( (j, i) \) entry of \( A^T \), for \( i, \, j \in \{1, 2, \ldots, m\} \). Simply stated, \( A^T\) is the matrix whose rows are the columns of \( A \). For the theorem that follows, we need to remember that \( (A B)^T = B^T A^T \) for \( A \in \R^{m \times n} \) and \( B \in \R^{n \times k} \), and \( \left(A^T\right)^{-1} = \left(A^{-1}\right)^T \) if \( A \in \R^{n \times n} \) is invertible.
Matrices \( A, \, B \in \R^{n \times n} \) are congruent if there exists an invertible \( P \in \R^{n \times n} \) such that \( B = P^T A P \). Congruence is an equivalence relation on \( \R^{n \times n} \)
Proof
If \( A \in \R^{n \times n} \) then \( A = I^T A I \), where again \( I \) is the \( n \times n \) identity matrix, so \( A \) is congruent to itself. Suppose that \( A, \, B \in \R^{n \times n} \) and that \( A \) is congruent to \( B \) so that \( B = P^T A P\) for some invertible \( P \in \R^{n \times n} \). Then \( A = \left(P^T\right)^{-1} B P^{-1} = \left(P^{-1}\right)^T B P^{-1} \) so \( B \) is congruent to \( A \). Finally, suppose that \( A, \, B, \, C \in R^{n \times n} \) and that \( A \) is congruent to \( B \) and that \( B \) is congruent to \( C \). Then \( B = P^T A P \) and \( C = Q^T B Q \) for some invertible \( P, \, Q \in R^{n \times n} \). Then \( C = Q^T P^T A P Q = (P Q)^T A (P Q) \), so \( A \) is congruent to \( C \).
Congruence is important in the study of orthogonal matrices and change of basis. Of course, the term congruence applied to matrices should not be confused with the same term applied to integers.
Number Systems
Equivalence relations play an important role in the construction of complex mathematical structures from simpler ones. Often the objects in the new structure are equivalence classes of objects constructed from the simpler structures, modulo an equivalence relation that captures the essential properties of the new objects.
The construction of number systems is a prime example of this general idea. The next exercise explores the construction of rational numbers from integers.
Define a relation \(\approx\) on \(\Z \times \N_+\) by \((j, k) \approx (m, n)\) if and only if \(j\,n = k\,m\).
- \(\approx\) is an equivalence relation.
- Define \(\frac{m}{n} = [(m, n)]\), the equivalence class generated by \((m, n)\), for \(m \in \Z\) and \(n \in \N_+\). This definition captures the essential properties of the rational numbers.
Proof
- For \( (m, n) \in \Z \times \N_+ \), \( m n = n m \) of course, so \( (m, n) \approx (m, n) \). Hence \( \approx \) is reflexive. If \( (j, k), \, (m, n) \in \Z \times \N_+ \) and \( (j, k) \approx (m, n) \), then \( j n = k m \) so trivially \( m k = n j\), and hence \( (m, n) \approx (j, k) \). Thus \( \approx \) is symmetric. Finally, suppose that \( (j, k), \, (m, n), \, (p, q) \in \Z \times \N_+ \) and that \( (j, k) \approx (m, n) \) and \( (m, n) \approx (p, q) \). Then \( j n = k m \) and \( m q = n p \), so \( j n p = k m p \) which implies \( j m q = k m p \), and so \( j q = k p \). Hence \( (j, k) \approx (p, q) \) so \( \approx \) is transitive.
- Suppose that \(\frac{j}{k}\) and \(\frac{m}{n} \) are rational numbers in the usual, informal sense, where \( j, \, m \in \Z \) and \( k, \, n \in \N_+ \). Then \( \frac{j}{k} = \frac{m}{n} \) if and only if \( j n = k m \) if and only if \( (j, k) \approx (m, n) \), so it makes sense to define \( \frac{m}{n} \) as the equivalence class generated by \( (m, n) \). Addition and multiplication are defined in the usual way: if \( (j, k), \, (m, n) \in \Z \times \N_+ \) then \[ \frac{j}{k} + \frac{m}{n} = \frac{j n + m k}{k n}, \ \ \frac{j}{k} \cdot \frac{m}{n} = \frac{j m}{k n} \] The definitions are consistent; that is they do not depend on the particular representations of the equivalence classes.


