3.3: Card Shuffling
- Page ID
- 3132
Card Shuffling
Much of this section is based upon an article by Brad Mann,28 which is an exposition of an article by David Bayer and Persi Diaconis.29
Riffle Shuffles
Given a deck of \(n\) cards, how many times must we shuffle it to make it “random"? Of course, the answer depends upon the method of shuffling which is used and what we mean by “random." We shall begin the study of this question by considering a standard model for the riffle shuffle.
We begin with a deck of \(n\) cards, which we will assume are labelled in increasing order with the integers from 1 to \(n\). A riffle shuffle consists of a cut of the deck into two stacks and an interleaving of the two stacks. For example, if \(n = 6\), the initial ordering is \((1, 2, 3, 4, 5, 6)\), and a cut might occur between cards 2 and 3. This gives rise to two stacks, namely \((1, 2)\) and \((3, 4, 5, 6)\). These are interleaved to form a new ordering of the deck. For example, these two stacks might form the ordering \((1, 3, 4, 2, 5, 6)\). In order to discuss such shuffles, we need to assign a probability distribution to the set of all possible shuffles. There are several reasonable ways in which this can be done. We will give several different assignment strategies, and show that they are equivalent. (This does not mean that this assignment is the only reasonable one.) First, we assign the binomial probability \(b(n, 1/2, k)\) to the event that the cut occurs after the \(k\)th card. Next, we assume that all possible interleavings, given a cut, are equally likely. Thus, to complete the assignment of probabilities, we need to determine the number of possible interleavings of two stacks of cards, with \(k\) and \(n-k\) cards, respectively.
We begin by writing the second stack in a line, with spaces in between each pair of consecutive cards, and with spaces at the beginning and end (so there are \(n-k+1\) spaces). We choose, with replacement, \(k\) of these spaces, and place the cards from the first stack in the chosen spaces. This can be done in
\[ n \choose{k} \]
ways. Thus, the probability of a given interleaving should be
\[{1\over{ n\choose{k} }}.\]
Next, we note that if the new ordering is not the identity ordering, it is the result of a unique cut-interleaving pair. If the new ordering is the identity, it is the result of any one of \(n+1\) cut-interleaving pairs.
We define a in an ordering to be a maximal subsequence of consecutive integers in increasing order. For example, in the ordering \[(2, 3, 5, 1, 4, 7, 6)\ ,\] there are 4 rising sequences; they are \((1)\), \((2, 3, 4)\), \((5, 6)\), and \((7)\). It is easy to see that an ordering is the result of a riffle shuffle applied to the identity ordering if and only if it has no more than two rising sequences. (If the ordering has two rising sequences, then these rising sequences correspond to the two stacks induced by the cut, and if the ordering has one rising sequence, then it is the identity ordering.) Thus, the sample space of orderings obtained by applying a riffle shuffle to the identity ordering is naturally described as the set of all orderings with at most two rising sequences.
It is now easy to assign a probability distribution to this sample space. Each ordering with two rising sequences is assigned the value
\[ \frac{b(n, 1/2, k)}{n \choose{k}} = \frac{1}{2^n},\]
and the identity ordering is assigned the value
\[{n+1}\over{2^n} .\]
There is another way to view a riffle shuffle. We can imagine starting with a deck cut into two stacks as before, with the same probabilities assignment as before i.e., the binomial distribution. Once we have the two stacks, we take cards, one by one, off of the bottom of the two stacks, and place them onto one stack. If there are \(k_1\) and \(k_2\) cards, respectively, in the two stacks at some point in this process, then we make the assumption that the probabilities that the next card to be taken comes from a given stack is proportional to the current stack size. This implies that the probability that we take the next card from the first stack equals
\[{k_1}\over{k_1 + k_2} ,\]
and the corresponding probability for the second stack is
\[{k_2}\over{k_1 + k_2} .\]
We shall now show that this process assigns the uniform probability to each of the possible interleavings of the two stacks.
Suppose, for example, that an interleaving came about as the result of choosing cards from the two stacks in some order. The probability that this result occurred is the product of the probabilities at each point in the process, since the choice of card at each point is assumed to be independent of the previous choices. Each factor of this product is of the form
\[\dfrac{k_1}{k_1+k_2}\]
where \(i = 1\) or \(2\), and the denominator of each factor equals the number of cards left to be chosen. Thus, the denominator of the probability is just \(n!\). At the moment when a card is chosen from a stack that has \(i\) cards in it, the numerator of the corresponding factor in the probability is \(i\), and the number of cards in this stack decreases by 1. Thus, the numerator is seen to be \(k!(n-k)!\), since all cards in both stacks are eventually chosen. Therefore, this process assigns the probability \[ {1\over{ n\choose{k} } }\]
to each possible interleaving.
We now turn to the question of what happens when we riffle shuffle \(s\) times. It should be clear that if we start with the identity ordering, we obtain an ordering with at most \(2^s\) rising sequences, since a riffle shuffle creates at most two rising sequences from every rising sequence in the starting ordering. In fact, it is not hard to see that each such ordering is the result of \(s\) riffle shuffles. The question becomes, then, in how many ways can an ordering with \(r\) rising sequences come about by applying \(s\) riffle shuffles to the identity ordering? In order to answer this question, we turn to the idea of an \(a\)-shuffle.
\(a\)-Shuffles
There are several ways to visualize an \(a\)-shuffle. One way is to imagine a creature with \(a\) hands who is given a deck of cards to riffle shuffle. The creature naturally cuts the deck into \(a\) stacks, and then riffles them together. (Imagine that!) Thus, the ordinary riffle shuffle is a 2-shuffle. As in the case of the ordinary 2-shuffle, we allow some of the stacks to have 0 cards. Another way to visualize an \(a\)-shuffle is to think about its inverse, called an \(a\)-unshuffle. This idea is described in the proof of the next theorem.
We will now show that an \(a\)-shuffle followed by a \(b\)-shuffle is equivalent to an \(ab\)-shuffle. This means, in particular, that \(s\) riffle shuffles in succession are equivalent to one \(2^s\)-shuffle. This equivalence is made precise by the following theorem.
Let \(a\) and \(b\) be two positive integers. Let \(S_{a,b}\) be the set of all ordered pairs in which the first entry is an \(a\)-shuffle and the second entry is a \(b\)-shuffle. Let \(S_{ab}\) be the set of all \(ab\)-shuffles. Then there is a 1-1 correspondence between \(S_{a,b}\) and \(S_{ab}\) with the following property. Suppose that \((T_1, T_2)\) corresponds to \(T_3\). If \(T_1\) is applied to the identity ordering, and \(T_2\) is applied to the resulting ordering, then the final ordering is the same as the ordering that is obtained by applying \(T_3\) to the identity ordering.
Proof. The easiest way to describe the required correspondence is through the idea of an unshuffle. An \(a\)-unshuffle begins with a deck of \(n\) cards. One by one, cards are taken from the top of the deck and placed, with equal probability, on the bottom of any one of \(a\) stacks, where the stacks are labelled from 0 to \(a-1\). After all of the cards have been distributed, we combine the stacks to form one stack by placing stack \(i\) on top of stack \(i+1\), for \(0 \le i \le a-1\). It is easy to see that if one starts with a deck, there is exactly one way to cut the deck to obtain the \(a\) stacks generated by the \(a\)-unshuffle, and with these \(a\) stacks, there is exactly one way to interleave them to obtain the deck in the order that it was in before the unshuffle was performed. Thus, this \(a\)-unshuffle corresponds to a unique \(a\)-shuffle, and this \(a\)-shuffle is the inverse of the original \(a\)-unshuffle.
If we apply an \(ab\)-unshuffle \(U_3\) to a deck, we obtain a set of \(ab\) stacks, which are then combined, in order, to form one stack. We label these stacks with ordered pairs of integers, where the first coordinate is between 0 and \(a-1\), and the second coordinate is between 0 and \(b-1\). Then we label each card with the label of its stack. The number of possible labels is \(ab\), as required. Using this labelling, we can describe how to find a \(b\)-unshuffle and an \(a\)-unshuffle, such that if these two unshuffles are applied in this order to the deck, we obtain the same set of \(ab\) stacks as were obtained by the \(ab\)-unshuffle.
To obtain the \(b\)-unshuffle \(U_2\), we sort the deck into \(b\) stacks, with the \(i\)th stack containing all of the cards with second coordinate \(i\), for \(0 \le i \le b-1\). Then these stacks are combined to form one stack. The \(a\)-unshuffle \(U_1\) proceeds in the same manner, except that the first coordinates of the labels are used. The resulting \(a\) stacks are then combined to form one stack.
The above description shows that the cards ending up on top are all those labelled \((0, 0)\). These are followed by those labelled \((0, 1),\ (0, 2),\) \(\ \ldots,\ (0, b - 1),\ (1, 0),\ (1,1),\ldots,\ (a-1, b-1)\). Furthermore, the relative order of any pair of cards with the same labels is never altered. But this is exactly the same as an \(ab\)-unshuffle, if, at the beginning of such an unshuffle, we label each of the cards with one of the labels \((0, 0),\ (0, 1),\ \ldots,\ (0, b-1),\ (1, 0),\ (1,1),\ \ldots,\ (a-1, b-1)\). This completes the proof.
In Figure [\(\PageIndex{1}\), we show the labels for a 2-unshuffle of a deck with 10 cards. There are 4 cards with the label 0 and 6 cards with the label 1, so if the 2-unshuffle is performed, the first stack will have 4 cards and the second stack will have 6 cards. When this unshuffle is performed, the deck ends up in the identity ordering.
In Figure \(\PageIndex{2}\), we show the labels for a 4-unshuffle of the same deck (because there are four labels being used). This figure can also be regarded as an example of a pair of 2-unshuffles, as described in the proof above. The first 2-unshuffle will use the second coordinate of the labels to determine the stacks. In this case, the two stacks contain the cards whose values are
\[\{5, 1, 6, 2, 7\} {\rm and} \{8, 9, 3, 4, 10\}.\]
After this 2-unshuffle has been performed, the deck is in the order shown in Figure [fig 3.14], as the reader should check. If we wish to perform a 4-unshuffle on the deck, using the labels shown, we sort the cards lexicographically, obtaining the four stacks
\[\{1, 2\},\ \{3, 4\},\ \{5, 6, 7\},\ {\rm and}\ \{8, 9, 10\}.\]
When these stacks are combined, we once again obtain the identity ordering of the deck. The point of the above theorem is that both sorting procedures always lead to the same initial ordering.


If \(D\) is any ordering that is the result of applying an \(a\)-shuffle and then a \(b\)-shuffle to the identity ordering, then the probability assigned to \(D\) by this pair of operations is the same as the probability assigned to \(D\) by the process of applying an \(ab\)-shuffle to the identity ordering.
Proof. Call the sample space of \(a\)-shuffles \(S_a\). If we label the stacks by the integers from \(0\) to \(a-1\), then each cut-interleaving pair, i.e., shuffle, corresponds to exactly one \(n\)-digit base \(a\) integer, where the \(i\)th digit in the integer is the stack of which the \(i\)th card is a member. Thus, the number of cut-interleaving pairs is equal to the number of \(n\)-digit base \(a\) integers, which is \(a^n\). Of course, not all of these pairs leads to different orderings. The number of pairs leading to a given ordering will be discussed later. For our purposes it is enough to point out that it is the cut-interleaving pairs that determine the probability assignment.
The previous theorem shows that there is a 1-1 correspondence between \(S_{a,b}\) and \(S_{ab}\). Furthermore, corresponding elements give the same ordering when applied to the identity ordering. Given any ordering \(D\), let \(m_1\) be the number of elements of \(S_{a,b}\) which, when applied to the identity ordering, result in \(D\). Let \(m_2\) be the number of elements of \(S_{ab}\) which, when applied to the identity ordering, result in \(D\). The previous theorem implies that \(m_1 = m_2\). Thus, both sets assign the probability
\[\dfrac{m_1}{\left ( ab \right )^{n}}\]
to \(D\). This completes the proof.
Connection with the Birthday Problem
There is another point that can be made concerning the labels given to the cards by the successive unshuffles. Suppose that we 2-unshuffle an \(n\)-card deck until the labels on the cards are all different. It is easy to see that this process produces each permutation with the same probability, i.e., this is a random process. To see this, note that if the labels become distinct on the \(s\)th 2-unshuffle, then one can think of this sequence of 2-unshuffles as one \(2^s\)-unshuffle, in which all of the stacks determined by the unshuffle have at most one card in them (remember, the stacks correspond to the labels). If each stack has at most one card in it, then given any two cards in the deck, it is equally likely that the first card has a lower or a higher label than the second card. Thus, each possible ordering is equally likely to result from this \(2^s\)-unshuffle.
Let \(T\) be the random variable that counts the number of 2-unshuffles until all labels are distinct. One can think of \(T\) as giving a measure of how long it takes in the unshuffling process until randomness is reached. Since shuffling and unshuffling are inverse processes, \(T\) also measures the number of shuffles necessary to achieve randomness. Suppose that we have an \(n\)-card deck, and we ask for \(P(T \le s)\). This equals \(1 - P(T > s)\). But \(T > s\) if and only if it is the case that not all of the labels after \(s\) 2-unshuffles are distinct. This is just the birthday problem; we are asking for the probability that at least two people have the same birthday, given that we have \(n\) people and there are \(2^s\) possible birthdays. Using our formula from Example [exam 3.3], we find that
\[P(T > s) = 1 - {2^s \choose n} \frac{n!}{2^{sn}}.\]
In Chapter [chp 6], we will define the average value of a random variable. Using this idea, and the above equation, one can calculate the average value of the random variable \(T\) (see Exercise [sec 6.1].[exer 6.1.42]). For example, if \(n = 52\), then the average value of \(T\) is about 11.7. This means that, on the average, about 12 riffle shuffles are needed for the process to be considered random.
Cut-Interleaving Pairs and Orderings
As was noted in the proof of Theorem [thm 3.3.2], not all of the cut-interleaving pairs lead to different orderings. However, there is an easy formula which gives the number of such pairs that lead to a given ordering.
If an ordering of length \(n\) has \(r\) rising sequences, then the number of cut-interleaving pairs under an \(a\)-shuffle of the identity ordering which lead to the ordering is
\[ { n + a - r \choose{n} }.\]
Proof:To see why this is true, we need to count the number of ways in which the cut in an \(a\)-shuffle can be performed which will lead to a given ordering with \(r\) rising sequences. We can disregard the interleavings, since once a cut has been made, at most one interleaving will lead to a given ordering. Since the given ordering has \(r\) rising sequences, \(r-1\) of the division points in the cut are determined. The remaining \(a - 1 - (r - 1) = a - r\) division points can be placed anywhere. The number of places to put these remaining division points is \(n+1\) (which is the number of spaces between the consecutive pairs of cards, including the positions at the beginning and the end of the deck). These places are chosen with repetition allowed, so the number of ways to make these choices is
\[{n + a - r \choose{a-r}} = {n + a - r \choose{n}} .\]
In particular, this means that if \(D\) is an ordering that is the result of applying an \(a\)-shuffle to the identity ordering, and if \(D\) has \(r\) rising sequences, then the probability assigned to \(D\) by this process is
\[{ {n + a - r\choose{n}} \over{a^n}}.\]
This completes the proof.
The above theorem shows that the essential information about the probability assigned to an ordering under an \(a\)-shuffle is just the number of rising sequences in the ordering. Thus, if we determine the number of orderings which contain exactly \(r\) rising sequences, for each \(r\) between 1 and \(n\), then we will have determined the distribution function of the random variable which consists of applying a random \(a\)-shuffle to the identity ordering.
The number of orderings of \(\{1, 2, \ldots, n\}\) with \(r\) rising sequences is denoted by \(A(n, r)\), and is called an Eulerian number. There are many ways to calculate the values of these numbers; the following theorem gives one recursive method which follows immediately from what we already know about \(a\)-shuffles.
Let \(a\) and \(n\) be positive integers. Then
\[a^n = \sum_{r = 1}^a {n + a - r \choose{n} } A(n, r). \]
Thus,
\[A(n, a) = a^n - \sum_{r = 1}^{a-1} { n + a - r \choose{n} }A(n, r) \]
In addition,
\[A(n, 1) = 1\]
Proof: The second equation can be used to calculate the values of the Eulerian numbers, and follows immediately from the Equation [eq 3.6]. The last equation is a consequence of the fact that the only ordering of \(\{1, 2, \ldots, n\}\) with one rising sequence is the identity ordering. Thus, it remains to prove Equation [eq 3.6]. We will count the set of \(a\)-shuffles of a deck with \(n\) cards in two ways. First, we know that there are \(a^n\) such shuffles (this was noted in the proof of Theorem . But there are \(A(n, r)\) orderings of \(\{1, 2, \ldots, n\}\) with \(r\) rising sequences, and Theorem states that for each such ordering, there are exactly
\[{ n+a-r \choose n}\]
cut-interleaving pairs that lead to the ordering. Therefore, the right-hand side of Equation [eq 3.6] counts the set of \(a\)-shuffles of an \(n\)-card deck. This completes theproof.
Random Orderings and Random Processes
We now turn to the second question that was asked at the beginning of this section: What do we mean by a “random" ordering? It is somewhat misleading to think about a given ordering as being random or not random. If we want to choose a random ordering from the set of all orderings of \(\{1, 2, \ldots, n\}\), we mean that we want every ordering to be chosen with the same probability, i.e., any ordering is as “random" as any other.
The word “random" should really be used to describe a process. We will say that a process that produces an object from a (finite) set of objects is a random process if each object in the set is produced with the same probability by the process. In the present situation, the objects are the orderings, and the process which produces these objects is the shuffling process. It is easy to see that no \(a\)-shuffle is really a random process, since if \(T_1\) and \(T_2\) are two orderings with a different number of rising sequences, then they are produced by an \(a\)-shuffle, applied to the identity ordering, with different probabilities.
Variation Distance
Instead of requiring that a sequence of shuffles yield a process which is random, we will define a measure that describes how far away a given process is from a random process. Let \(X\) be any process which produces an ordering of \(\{1, 2, \ldots, n\}\). Define \(f_X(\pi)\) be the probability that \(X\) produces the ordering \(\pi\). (Thus, \(X\) can be thought of as a random variable with distribution function \(f\).) Let \(\Omega_n\) be the set of all orderings of \(\{1, 2, \ldots, n\}\). Finally, let \(u(\pi) = 1/|\Omega_n|\) for all \(\pi \in \Omega_n\). The function \(u\) is the distribution function of a process which produces orderings and which is random. For each ordering \(\pi \in \Omega_n\), the quantity \[|f_X(\pi) - u(\pi)|\] is the difference between the actual and desired probabilities that \(X\) produces \(\pi\). If we sum this over all orderings \(\pi\) and call this sum \(S\), we see that \(S = 0\) if and only if \(X\) is random, and otherwise \(S\) is positive. It is easy to show that the maximum value of \(S\) is 2, so we will multiply the sum by \(1/2\) so that the value falls in the interval \([0, 1]\). Thus, we obtain the following sum as the formula for the between the two processes: \[\parallel f_X - u \parallel = {1\over 2}\sum_{\pi \in \Omega_n} |f_X(\pi) - u(\pi)| .\]
Now we apply this idea to the case of shuffling. We let \(X\) be the process of \(s\) successive riffle shuffles applied to the identity ordering. We know that it is also possible to think of \(X\) as one \(2^s\)-shuffle. We also know that \(f_X\) is constant on the set of all orderings with \(r\) rising sequences, where \(r\) is any positive integer. Finally, we know the value of \(f_X\) on an ordering with \(r\) rising sequences, and we know how many such orderings there are. Thus, in this specific case, we have
\[\parallel f_X - u \parallel = {1\over 2}\sum_{r=1}^n A(n, r) \biggl| {2^s + n - r\choose{n}}/2^{ns} - {1\over{n!}}\biggr| \]
Since this sum has only \(n\) summands, it is easy to compute this for moderate sized values of \(n\). For \(n = 52\), we obtain the list of values given in Table .
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 0.9999995334 |
| 5 | 0.9237329294 |
| 6 | 0.6135495966 |
| 7 | 0.3340609995 |
| 8 | 0.1671586419 |
| 9 | 0.0854201934 |
| 10 | 0.0429455489 |
| 11 | 0.0215023760 |
| 12 | 0.0107548935 |
| 13 | 0.0053779101 |
| 14 | 0.0026890130 |
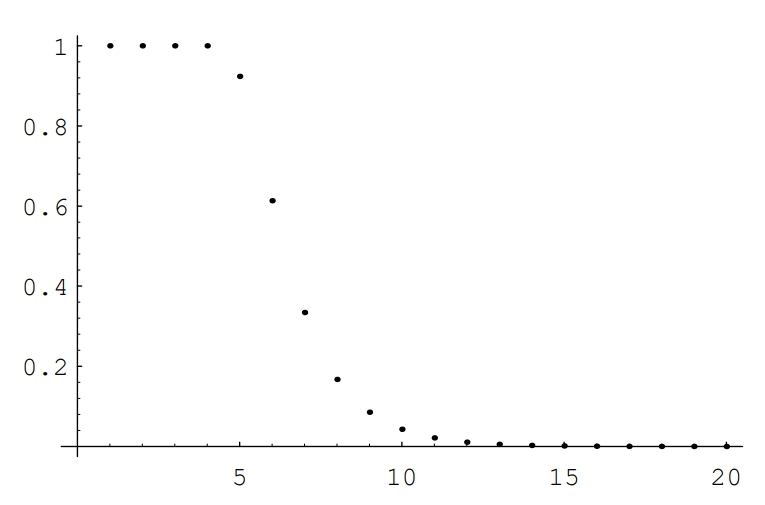
To help in understanding these data, they are shown in graphical form in Figure \(\PageIndex{1}\). The program VariationList produces the data shown in both Table \(\PageIndex{1}\) and Figure \(\PageIndex{1}\) One sees that until 5 shuffles have occurred, the output of \(X\) is very far from random. After 5 shuffles, the distance from the random process is essentially halved each time a shuffle occurs.
Given the distribution functions \(f_X(\pi)\) and \(u(\pi)\) as above, there is another way to view the variation distance \(\parallel f_X - u\parallel\). Given any event \(T\) (which is a subset of \(S_n\)), we can calculate its probability under the process \(X\) and under the uniform process. For example, we can imagine that \(T\) represents the set of all permutations in which the first player in a 7-player poker game is dealt a straight flush (five consecutive cards in the same suit). It is interesting to consider how much the probability of this event after a certain number of shuffles differs from the probability of this event if all permutations are equally likely. This difference can be thought of as describing how close the process \(X\) is to the random process with respect to the event \(T\).
Now consider the event \(T\) such that the absolute value of the difference between these two probabilities is as large as possible. It can be shown that this absolute value is the variation distance between the process \(X\) and the uniform process. (The reader is asked to prove this fact in Exercise .)
We have just seen that, for a deck of 52 cards, the variation distance between the 7-riffle shuffle process and the random process is about \(.334\). It is of interest to find an event \(T\) such that the difference between the probabilities that the two processes produce \(T\) is close to \(.334\). An event with this property can be described in terms of the game called New-Age Solitaire.
New-Age Solitaire
This game was invented by Peter Doyle. It is played with a standard 52-card deck. We deal the cards face up, one at a time, onto a discard pile. If an ace is encountered, say the ace of Hearts, we use it to start a Heart pile. Each suit pile must be built up in order, from ace to king, using only subsequently dealt cards. Once we have dealt all of the cards, we pick up the discard pile and continue. We define the Yin suits to be Hearts and Clubs, and the Yang suits to be Diamonds and Spades. The game ends when either both Yin suit piles have been completed, or both Yang suit piles have been completed. It is clear that if the ordering of the deck is produced by the random process, then the probability that the Yin suit piles are completed first is exactly 1/2.
Now suppose that we buy a new deck of cards, break the seal on the package, and riffle shuffle the deck 7 times. If one tries this, one finds that the Yin suits win about 75% of the time. This is 25% more than we would get if the deck were in truly random order. This deviation is reasonably close to the theoretical maximum of \(33.4\)% obtained above.
Why do the Yin suits win so often? In a brand new deck of cards, the suits are in the following order, from top to bottom: ace through king of Hearts, ace through king of Clubs, king through ace of Diamonds, and king through ace of Spades. Note that if the cards were not shuffled at all, then the Yin suit piles would be completed on the first pass, before any Yang suit cards are even seen. If we were to continue playing the game until the Yang suit piles are completed, it would take 13 passes through the deck to do this. Thus, one can see that in a new deck, the Yin suits are in the most advantageous order and the Yang suits are in the least advantageous order. Under 7 riffle shuffles, the relative advantage of the Yin suits over the Yang suits is preserved to a certain extent.
Exercises
Given any ordering \(\sigma\) of \(\{1, 2, \ldots, n\}\), we can define \(\sigma^{-1}\), the inverse ordering of \(\sigma\), to be the ordering in which the \(i\)th element is the position occupied by \(i\) in \(\sigma\). For example, if \(\sigma = (1, 3, 5, 2, 4, 7, 6)\), then \(\sigma^{-1} = (1, 4, 2, 5, 3, 7, 6)\). (If one thinks of these orderings as permutations, then \(\sigma^{-1}\) is the inverse of \(\sigma\).)
A occurs between two positions in an ordering if the left position is occupied by a larger number than the right position. It will be convenient to say that every ordering has a fall after the last position. In the above example, \(\sigma^{-1}\) has four falls. They occur after the second, fourth, sixth, and seventh positions. Prove that the number of rising sequences in an ordering \(\sigma\) equals the number of falls in \(\sigma^{-1}\).
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
Show that if we start with the identity ordering of \(\{1, 2, \ldots, n\}\), then the probability that an \(a\)-shuffle leads to an ordering with exactly \(r\) rising sequences equals
\[\dfrac{\left(\begin{array}{c}n+a-r \\ n\end{array}\right)}{a^n} A(n, r)\],
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
Let \(D\) be a deck of \(n\) cards. We have seen that there are \(a^n\) \(a\)-shuffles of \(D\). A coding of the set of \(a\)-unshuffles was given in the proof of Theorem [thm 3.3.1]. We will now give a coding of the \(a\)-shuffles which corresponds to the coding of the \(a\)-unshuffles. Let \(S\) be the set of all \(n\)-tuples of integers, each between 0 and \(a-1\). Let \(M = (m_1, m_2, \ldots, m_n)\) be any element of \(S\). Let \(n_i\) be the number of \(i\)’s in \(M\), for \(0 \le i \le a-1\). Suppose that we start with the deck in increasing order (i.e., the cards are numbered from 1 to \(n\)). We label the first \(n_0\) cards with a 0, the next \(n_1\) cards with a 1, etc. Then the \(a\)-shuffle corresponding to \(M\) is the shuffle which results in the ordering in which the cards labelled \(i\) are placed in the positions in \(M\) containing the label \(i\). The cards with the same label are placed in these positions in increasing order of their numbers. For example, if \(n = 6\) and \(a = 3\), let \(M = (1, 0, 2, 2, 0, 2)\). Then \(n_0 = 2,\ n_1 = 1,\) and \(n_2 = 3\). So we label cards 1 and 2 with a 0, card 3 with a 1, and cards 4, 5, and 6 with a 2. Then cards 1 and 2 are placed in positions 2 and 5, card 3 is placed in position 1, and cards 4, 5, and 6 are placed in positions 3, 4, and 6, resulting in the ordering \((3, 1, 4, 5, 2, 6)\).
- Using this coding, show that the probability that in an \(a\)-shuffle, the first card (i.e., card number 1) moves to the \(i\)th position, is given by the following expression: \[\frac{(a-1)^{i-1} a^{n-i}+(a-2)^{i-1}(a-1)^{n-i}+\cdots+1^{i-1} 2^{n-i}}{a^n}\].
- Give an accurate estimate for the probability that in three riffle shuffles of a 52-card deck, the first card ends up in one of the first 26 positions. Using a computer, accurately estimate the probability of the same event after seven riffle shuffles.
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
Let \(X\) denote a particular process that produces elements of \(S_n\), and let \(U\) denote the uniform process. Let the distribution functions of these processes be denoted by \(f_X\) and \(u\), respectively. Show that the variation distance \(\parallel f_X - u\parallel\) is equal to \[\max_{T \subset S_n} \sum_{\pi \in T} \Bigl(f_X(\pi) - u(\pi)\Bigr).\]
: Write the permutations in \(S_n\) in decreasing order of the difference \(f_X(\pi) - u(\pi)\).
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.
Consider the process described in the text in which an \(n\)-card deck is repeatedly labelled and 2-unshuffled, in the manner described in the proof of Theorem ]. (See Figures ] and .) The process continues until the labels are all different. Show that the process never terminates until at least \(\lceil \log_2(n) \rceil\) unshuffles have been done.
- Answer
-
Add answer text here and it will automatically be hidden if you have a "AutoNum" template active on the page.


