20.8: Appendix-

Last updated
Save as PDF

Page ID: 8824

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

20.8.1 Rejection sampling

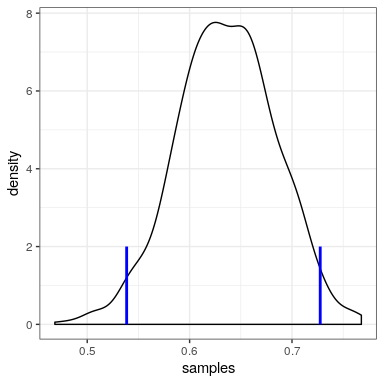
We will generate samples from our posterior distribution using a simple algorithm known as rejection sampling. The idea is that we choose a random value of x (in this case $p_{r e s p o n d} 20.6 shows an example of a histogram of samples using rejection sampling, along with the 95% credible intervals obtained using this method.$

# Compute credible intervals for example

nsamples <- 100000

# create random uniform variates for x and y
x <- runif(nsamples)
y <- runif(nsamples)

# create f(x)
fx <- dbinom(x = nResponders, size = 100, prob = x)

# accept samples where y < f(x)
accept <- which(y < fx)
accepted_samples <- x[accept]

credible_interval <- quantile(x = accepted_samples, 
                              probs = c(0.025, 0.975))
kable(credible_interval)

	x
2.5%	0.54
98%	0.73

Figure 20.6: Rejection sampling example.The black line shows the density of all possible values of p(respond); the blue lines show the 2.5th and 97.5th percentiles of the distribution, which represent the 95 percent credible interval for the estimate of p(respond).