1.8: Considering Categorical Data
- Page ID
- 305
Like numerical data, categorical data can also be organized and analyzed. In this section, we will introduce tables and other basic tools for categorical data that are used throughout this book. The email50 data set represents a sample from a larger email data set called email. This larger data set contains information on 3,921 emails. In this section we will examine whether the presence of numbers, small or large, in an email provides any useful value in classifying email as spam or not spam.
Contingency Tables and Bar Plots
Table 1.32 summarizes two variables: spam and number. Recall that number is a categorical variable that describes whether an email contains no numbers, only small numbers (values under 1 million), or at least one big number (a value of 1 million or more). A table that summarizes data for two categorical variables in this way is called a contingency table. Each value in the table represents the number of times a particular combination of variable outcomes occurred. For example, the value 149 corresponds to the number of emails in the data set that are spam and had no number listed in the email. Row and column totals are also included. The row totals provide the total counts across each row (e.g. 149 + 168 + 50 = 367), and column totals are total counts down each column.
| number | ||||
|---|---|---|---|---|
| none | small | big | Total | |
| spam | 149 | 168 | 50 | 367 |
| not spam | 400 | 2659 | 495 | 3554 |
| Total | 549 | 2827 | 545 | 3921 |
A table for a single variable is called a frequency table. Table 1.33 is a frequency table for the number variable. If we replaced the counts with percentages or proportions, the table would be called a relative frequency table.
| none | small | big | Total |
|---|---|---|---|
| 549 | 2827 | 545 | 3921 |
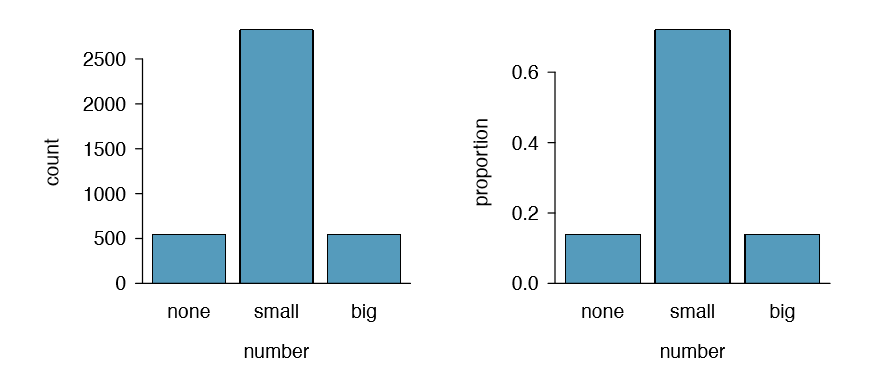
A bar plot is a common way to display a single categorical variable. The left panel of Figure 1.34 shows a bar plot for the number variable. In the right panel, the counts are converted into proportions (e.g. 549/3921 = 0.140 for none), showing the proportion of observations that are in each level (i.e. in each category).
41Note: answers will vary. There is a very strong correspondence between high earning and metropolitan areas. You might look for large cities you are familiar with and try to spot them on the map as dark spots.
Row and Column Proportions
Table 1.35 shows the row proportions for Table 1.32. The row proportions are computed as the counts divided by their row totals. The value 149 at the intersection of spam and none is replaced by 149/367 = 0.406, i.e. 149 divided by its row total, 367. So what does 0.406 represent? It corresponds to the proportion of spam emails in the sample that do not have any numbers.
| none | small | big | Total | |
|---|---|---|---|---|
| spam | 149/367 = 0.406 | 168/367 = 0.458 | 50/367 = 0.136 | 1.000 |
| not spam | 400/3554 = 0.113 | 2657/3554 = 0.748 | 495/3554 = 0.139 | 1.000 |
| Total | 549/3921 = 0.140 | 2827/3921 = 0.721 | 545/3921 = 0.139 | 1.000 |
A contingency table of the column proportions is computed in a similar way, where each column proportion is computed as the count divided by the corresponding column total. Table 1.36 shows such a table, and here the value 0.271 indicates that 27.1% of emails with no numbers were spam. This rate of spam is much higher compared to emails with only small numbers (5.9%) or big numbers (9.2%). Because these spam rates vary between the three levels of number (none, small, big), this provides evidence that the spam and number variables are associated.
| none | small | big | Total | |
|---|---|---|---|---|
| spam | 149/549 = 0.271 | 168/2827 = 0.059 | 50/545 = 0.092 | 367/3921 = 0.094 |
| not spam | 400/549 = 0.729 | 2659/2827 = 0.941 | 495/545 = 0.908 | 3684/3921 = 0.906 |
| Total | 1.000 | 1.000 | 1.000 | 1.000 |
We could also have checked for an association between spam and number in Table 1.35 using row proportions. When comparing these row proportions, we would look down columns to see if the fraction of emails with no numbers, small numbers, and big numbers varied from spam to not spam.
Exercise \(\PageIndex{1}\)
What does 0.458 represent in Table 1.35? What does 0.059 represent in Table 1.36?
Solution
0.458 represents the proportion of spam emails that had a small number. 0.058 represents the fraction of emails with small numbers that are spam.
Exercise \(\PageIndex{2}\)
What does 0.139 at the intersection of not spam and big represent in Table 1.35? What does 0.908 represent in the Table 1.36?
Solution
0.139 represents the fraction of non-spam email that had a big number. 0.908 represents the fraction of emails with big numbers that are non-spam emails.
Example \(\PageIndex{1}\)
Data scientists use statistics to filter spam from incoming email messages. By noting specific characteristics of an email, a data scientist may be able to classify some emails as spam or not spam with high accuracy. One of those characteristics is whether the email contains no numbers, small numbers, or big numbers. Another characteristic is whether or not an email has any HTML content. A contingency table for the spam and format variables from the email data set are shown in Table 1.37. Recall that an HTML email is an email with the capacity for special formatting, e.g. bold text. In Table 1.37, which would be more helpful to someone hoping to classify email as spam or regular email: row or column proportions?
Such a person would be interested in how the proportion of spam changes within each email format. This corresponds to column proportions: the proportion of spam in plain text emails and the proportion of spam in HTML emails.
If we generate the column proportions, we can see that a higher fraction of plain text emails are spam (209/1195 = 17.5%) than compared to HTML emails (158/2726 = 5.8%). This information on its own is insufficient to classify an email as spam or not spam, as over 80% of plain text emails are not spam. Yet, when we carefully combine this information with many other characteristics, such as number and other variables, we stand a reasonable chance of being able to classify some email as spam or not spam. This is a topic we will return to in Chapter 8.
| text | HTML | Total | |
|---|---|---|---|
| spam | 209 | 158 | 367 |
| not spam | 986 | 2568 | 3554 |
| Total | 1195 | 2726 | 3921 |
Example \(\PageIndex{1}\) points out that row and column proportions are not equivalent. Before settling on one form for a table, it is important to consider each to ensure that the most useful table is constructed.
Exercise \(\PageIndex{3}\)
Look back to Tables 1.35 and 1.36. Which would be more useful to someone hoping to identify spam emails using the number variable?
Solution
The column proportions in Table 1.36 will probably be most useful, which makes it easier to see that emails with small numbers are spam about 5.9% of the time (relatively rare). We would also see that about 27.1% of emails with no numbers are spam, and 9.2% of emails with big numbers are spam.
Segmented Bar and Mosaic Plots
Contingency tables using row or column proportions are especially useful for examining how two categorical variables are related. Segmented bar and mosaic plots provide a way to visualize the information in these tables.
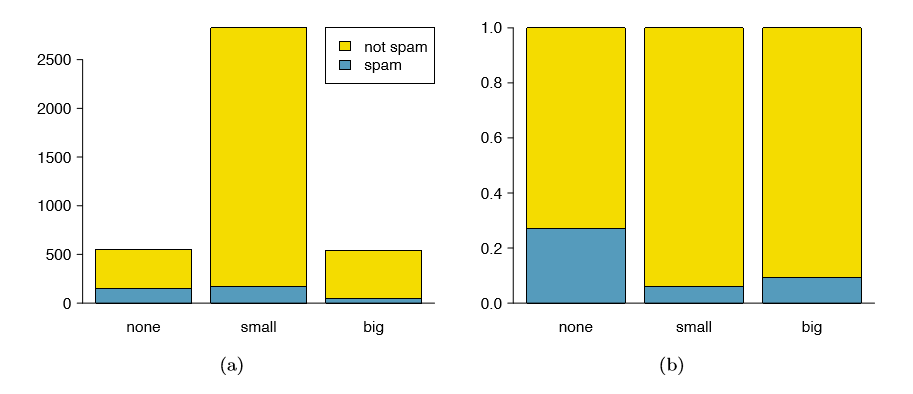
A segmented bar plot is a graphical display of contingency table information. For example, a segmented bar plot representing Table 1.36 is shown in Figure 1.38(a), where we have first created a bar plot using the number variable and then divided each group by the levels of spam. The column proportions of Table 1.36 have been translated into a standardized segmented bar plot in Figure 1.38(b), which is a helpful visualization of the fraction of spam emails in each level of number.
Example \(\PageIndex{2}\)
Examine both of the segmented bar plots. Which is more useful?
Solution
Figure 1.38(a) contains more information, but Figure 1.38(b) presents the information more clearly. This second plot makes it clear that emails with no number have a relatively high rate of spam email - about 27%! On the other hand, less than 10% of email with small or big numbers are spam.
Since the proportion of spam changes across the groups in Figure 1.38(b), we can conclude the variables are dependent, which is something we were also able to discern using table proportions. Because both the none and big groups have relatively few observations compared to the small group, the association is more difficult to see in Figure 1.38(a).
In some other cases, a segmented bar plot that is not standardized will be more useful in communicating important information. Before settling on a particular segmented bar plot, create standardized and non-standardized forms and decide which is more effective at communicating features of the data.
A mosaic plot is a graphical display of contingency table information that is similar to a bar plot for one variable or a segmented bar plot when using two variables. Figure 1.39(a) shows a mosaic plot for the number variable. Each column represents a level of number, and the column widths correspond to the proportion of emails of each number type. For instance, there are fewer emails with no numbers than emails with only small numbers, so
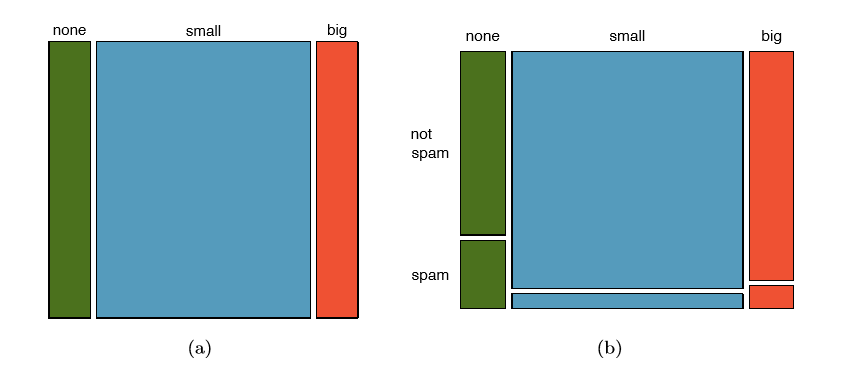
the no number email column is slimmer. In general, mosaic plots use box areas to represent the number of observations that box represents.
This one-variable mosaic plot is further divided into pieces in Figure 1.39(b) using the spam variable. Each column is split proportionally according to the fraction of emails that were spam in each number category. For example, the second column, representing emails with only small numbers, was divided into emails that were spam (lower) and not spam (upper). As another example, the bottom of the third column represents spam emails that had big numbers, and the upper part of the third column represents regular emails that had big numbers. We can again use this plot to see that the spam and number variables are associated since some columns are divided in different vertical locations than others, which was the same technique used for checking an association in the standardized version of the segmented bar plot.
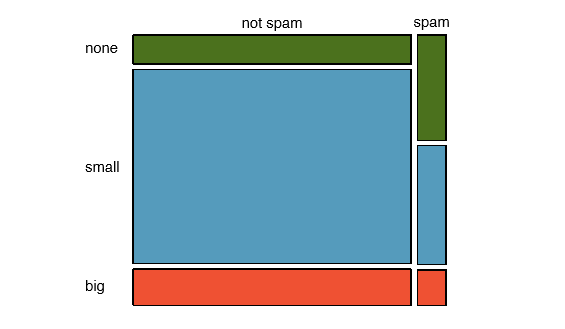
In a similar way, a mosaic plot representing row proportions of Table 1.32 could be constructed, as shown in Figure 1.40. However, because it is more insightful for this application to consider the fraction of spam in each category of the number variable, we prefer Figure 1.39(b).
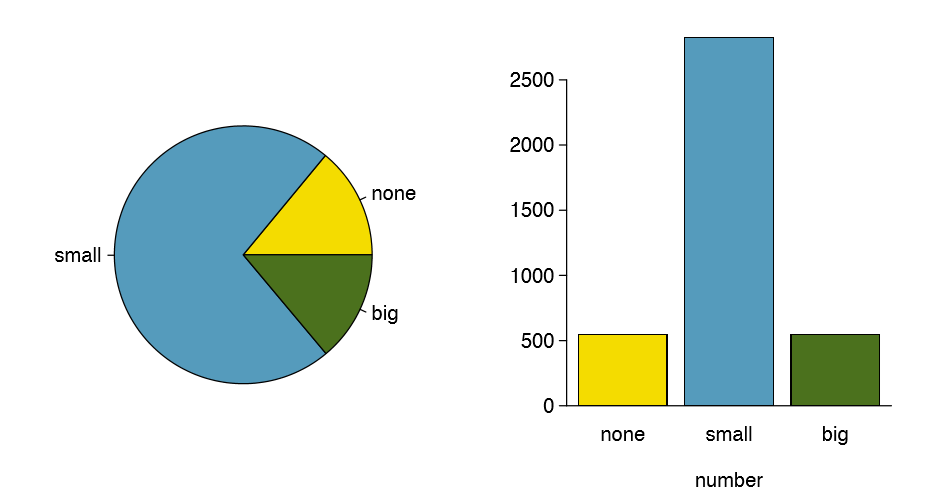
The only pie chart you will see in this book
While pie charts are well known, they are not typically as useful as other charts in a data analysis. A pie chart is shown in Figure 1.41 alongside a bar plot. It is generally more difficult to compare group sizes in a pie chart than in a bar plot, especially when categories have nearly identical counts or proportions. In the case of the none and big categories, the difference is so slight you may be unable to distinguish any difference in group sizes for either plot!
Comparing numerical data across groups
Some of the more interesting investigations can be considered by examining numerical data across groups. The methods required here aren't really new. All that is required is to make a numerical plot for each group. Here two convenient methods are introduced: side-by-side box plots and hollow histograms.
We will take a look again at the county data set and compare the median household income for counties that gained population from 2000 to 2010 versus counties that had no gain. While we might like to make a causal connection here, remember that these are observational data and so such an interpretation would be unjustified.
There were 2,041 counties where the population increased from 2000 to 2010, and there were 1,099 counties with no gain (all but one were a loss). A random sample of 100 counties from the first group and 50 from the second group are shown in Table 1.42 to give a better sense of some of the raw data.
| population gain |
no gain |
|---|---|
|
41.2 33.1 30.4 37.3 79.1 34.5 22.9 39.9 31.4 45.1 50.6 59.4 47.9 36.4 42.2 43.2 31.8 36.9 50.1 27.3 37.5 53.5 26.1 57.2 57.4 42.6 40.6 48.8 28.1 29.4 43.8 26 33.8 35.7 38.5 42.3 41.3 40.5 68.3 31 46.7 30.5 68.3 48.3 38.7 62 37.6 32.2 42.6 53.6 50.7 35.1 30.6 56.8 66.4 41.4 34.3 38.9 37.3 41.7 51.9 83.3 46.3 48.4 40.8 42.6 44.5 34 48.7 45.2 34.7 32.2 39.4 38.6 40 57.3 45.2 33.1 43.8 71.7 45.1 32.2 63.3 54.7 71.3 36.3 36.4 41 37 66.7 50.2 45.8 45.7 60.2 53.1 35.8 40.4 51.5 66.4 36.1 |
40.3 33.5 34.8 29.5 31.8 41.3 28 39.1 42.8 38.1 39.5 22.3 43.3 37.5 47.1 43.7 36.7 36 35.8 38.7 39.8 46 42.3 48.2 38.6 31.9 31.1 37.6 29.3 30.1 57.5 32.6 31.1 46.2 26.5 40.1 38.4 46.7 25.9 36.4 41.5 45.7 39.7 37 37.7 21.4 29.3 50.1 43.6 39.8 |
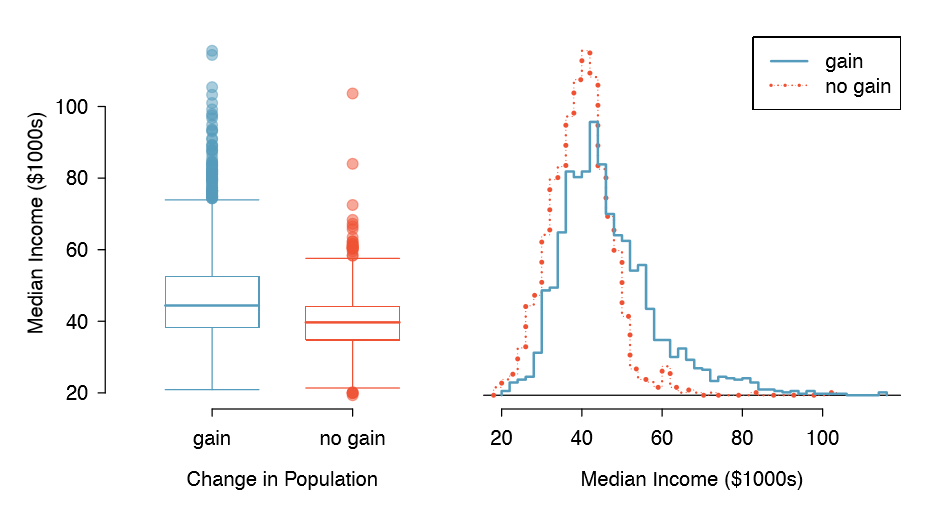
The side-by-side box plot is a traditional tool for comparing across groups. An example is shown in the left panel of Figure 1.43, where there are two box plots, one for each group, placed into one plotting window and drawn on the same scale.
Another useful plotting method uses hollow histograms to compare numerical data across groups. These are just the outlines of histograms of each group put on the same plot, as shown in the right panel of Figure 1.43.
Exercise \(\PageIndex{1}\)
Use the plots in Figure 1.43 to compare the incomes for counties across the two groups. What do you notice about the approximate center of each group? What do you notice about the variability between groups? Is the shape relatively consistent between groups? How many prominent modes are there for each group?
Solution
Answers may vary a little. The counties with population gains tend to have higher income (median of about $45,000) versus counties without a gain (median of about $40,000). The variability is also slightly larger for the population gain group. This is evident in the IQR, which is about 50% bigger in the gain group. Both distributions show slight to moderate right skew and are unimodal. There is a secondary small bump at about $60,000 for the no gain group, visible in the hollow histogram plot, that seems out of place. (Looking into the data set, we would nd that 8 of these 15 counties are in Alaska and Texas.) The box plots indicate there are many observations far above the median in each group, though we should anticipate that many observations will fall beyond the whiskers when using such a large data set.
Exercise \(\PageIndex{1}\)
What components of each plot in Figure 1.43 do you nd most useful?
Solution


