7.3: Areas Under Normal Distributions
- Page ID
- 2119
Learning Objectives
- State the proportion of a normal distribution within \(1\) and within \(2\) standard deviations of the mean
- Use the calculator "Calculate Area for a given \(X\)"
- Use the calculator "Calculate \(X\) for a given Area"
Areas under portions of a normal distribution can be computed by using calculus. Since this is a non-mathematical treatment of statistics, we will rely on computer programs and tables to determine these areas. Figure \(\PageIndex{1}\) shows a normal distribution with a mean of \(50\) and a standard deviation of \(10\). The shaded area between \(40\) and \(60\) contains \(68\%\) of the distribution.
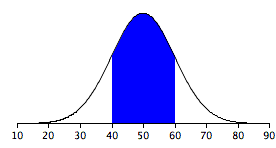
\(68\%\) of the area is within one standard deviation (\(10\)) of the mean (\(50\))
Figure \(\PageIndex{2}\) shows a normal distribution with a mean of \(100\) and a standard deviation of \(20\). As in Figure \(\PageIndex{1}\), \(68\%\) of the distribution is within one standard deviation of the mean.
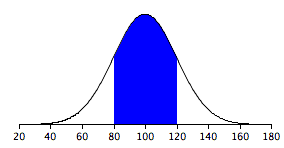
\(68\%\) of the area is within one standard deviation (\(20\)) of the mean (\(100\)).
The normal distributions shown in Figures \(\PageIndex{1}\) and \(\PageIndex{2}\) are specific examples of the general rule that \(68\%\) of the area of any normal distribution is within one standard deviation of the mean.
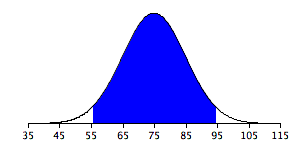
Figure \(\PageIndex{3}\) shows a normal distribution with a mean of \(75\) and a standard deviation of \(10\). The shaded area contains \(95\%\) of the area and extends from \(55.4\) to \(94.6\). For all normal distributions, \(95\%\) of the area is within \(1.96\) standard deviations of the mean. For quick approximations, it is sometimes useful to round off and use \(2\) rather than \(1.96\) as the number of standard deviations you need to extend from the mean so as to include \(95\%\) of the area.
The normal calculator can be used to calculate areas under the normal distribution. For example, you can use it to find the proportion of a normal distribution with a mean of \(90\) and a standard deviation of \(12\) that is above \(110\). Set the mean to \(90\) and the standard deviation to \(12\). Then enter "\(110\)" in the box to the right of the radio button "Above." At the bottom of the display you will see that the shaded area is \(0.0478\). See if you can use the calculator to find that the area between \(115\) and \(120\) is \(0.0124\).
Say you wanted to find the score corresponding to the \(75^{th}\) percentile of a normal distribution with a mean of \(90\) and a standard deviation of \(12\). Using the inverse normal calculator, you enter the parameters as shown in Figure \(\PageIndex{5}\) and find that the area below \(98.09\) is \(0.75\).
Normal and Inverse Normal Calculator


