2.5: Frequency Polygons
- Page ID
- 2086
Learning Objectives
- Create and interpret frequency polygons
- Create and interpret cumulative frequency polygons
- Create and interpret overlaid frequency polygons
Frequency polygons are a graphical device for understanding the shapes of distributions. They serve the same purpose as histograms, but are especially helpful for comparing sets of data. Frequency polygons are also a good choice for displaying cumulative frequency distributions.
To create a frequency polygon, start just as for histograms, by choosing a class interval. Then draw an \(X\)-axis representing the values of the scores in your data. Mark the middle of each class interval with a tick mark, and label it with the middle value represented by the class. Draw the \(Y\)-axis to indicate the frequency of each class. Place a point in the middle of each class interval at the height corresponding to its frequency. Finally, connect the points. You should include one class interval below the lowest value in your data and one above the highest value. The graph will then touch the \(X\)-axis on both sides.
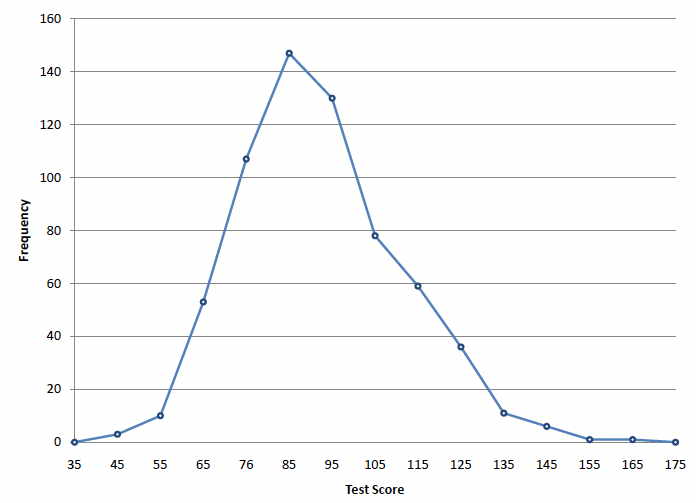
A frequency polygon for \(642\) psychology test scores shown in Figure \(\PageIndex{1}\) was constructed from the frequency table shown in Table \(\PageIndex{1}\).
| Lower Limit | Upper Limit | Count | Cumulative Count |
|---|---|---|---|
| 29.5 | 39.5 | 0 | 0 |
| 39.5 | 49.5 | 3 | 3 |
| 49.5 | 59.5 | 10 | 13 |
| 59.5 | 69.5 | 53 | 66 |
| 69.5 | 79.5 | 107 | 173 |
| 79.5 | 89.5 | 147 | 320 |
| 89.5 | 99.5 | 130 | 450 |
| 99.5 | 109.5 | 78 | 528 |
| 109.5 | 119.5 | 59 | 587 |
| 119.5 | 129.5 | 36 | 623 |
| 129.5 | 139.5 | 11 | 634 |
| 139.5 | 149.5 | 6 | 640 |
| 149.5 | 159.5 | 1 | 641 |
| 159.5 | 169.5 | 1 | 642 |
| 169.5 | 179.5 | 0 | 642 |
The first label on the \(X\)-axis is \(35\). This represents an interval extending from \(29.5\) to \(39.5\). Since the lowest test score is \(46\), this interval has a frequency of \(0\). The point labeled \(45\) represents the interval from \(39.5\) to \(49.5\). There are three scores in this interval. There are \(147\) scores in the interval that surrounds \(85\).
You can easily discern the shape of the distribution from Figure \(\PageIndex{1}\). Most of the scores are between \(65\) and \(115\). It is clear that the distribution is not symmetric inasmuch as good scores (to the right) trail off more gradually than poor scores (to the left). In the terminology of Chapter 3 (where we will study shapes of distributions more systematically), the distribution is skewed.
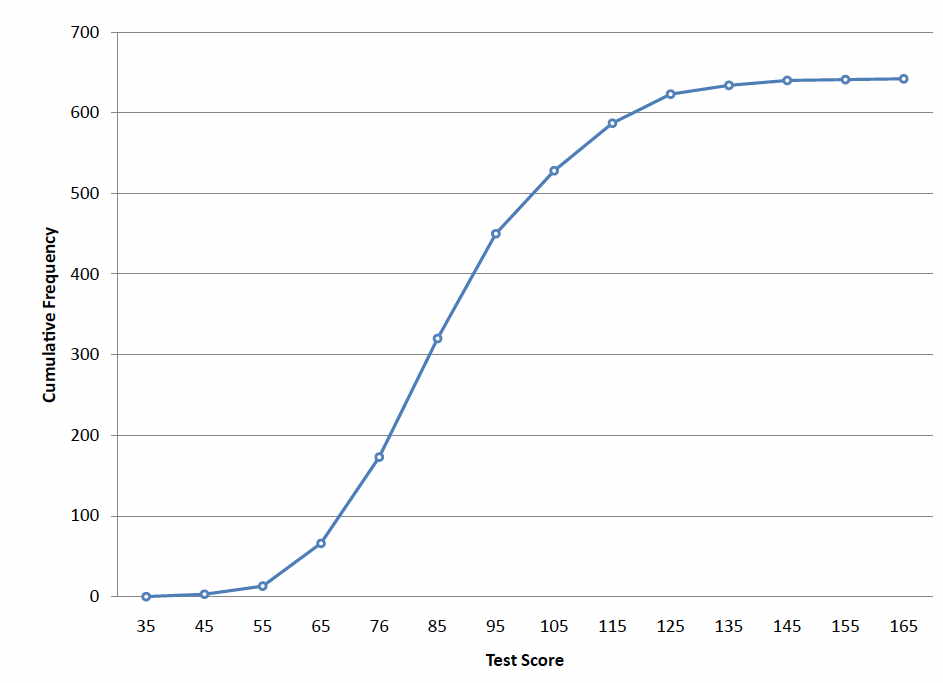
A cumulative frequency polygon for the same test scores is shown in Figure \(\PageIndex{2}\). The graph is the same as before except that the \(Y\) value for each point is the number of students in the corresponding class interval plus all numbers in lower intervals. For example, there are no scores in the interval labeled \(35\), three in the interval \(45\), and \(10\) in the interval \(55\). Therefore, the \(Y\) value corresponding to "\(55\)" is \(13\). Since \(642\) students took the test, the cumulative frequency for the last interval is \(642\).
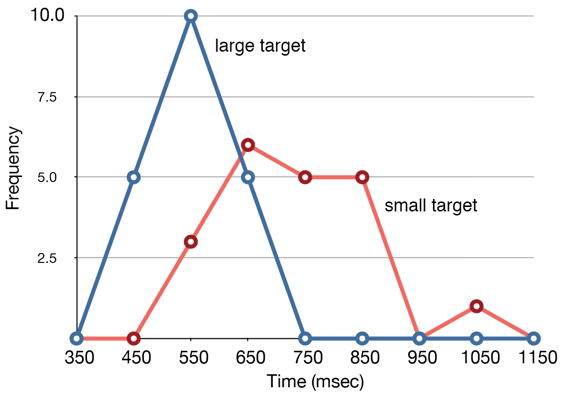
Frequency polygons are useful for comparing distributions. This is achieved by overlaying the frequency polygons drawn for different data sets. Figure \(\PageIndex{3}\) provides an example. The data come from a task in which the goal is to move a computer cursor to a target on the screen as fast as possible. On \(20\) of the trials, the target was a small rectangle; on the other \(20\), the target was a large rectangle. Time to reach the target was recorded on each trial. The two distributions (one for each target) are plotted together in Figure \(\PageIndex{3}\). The figure shows that, although there is some overlap in times, it generally took longer to move the cursor to the small target than to the large one.
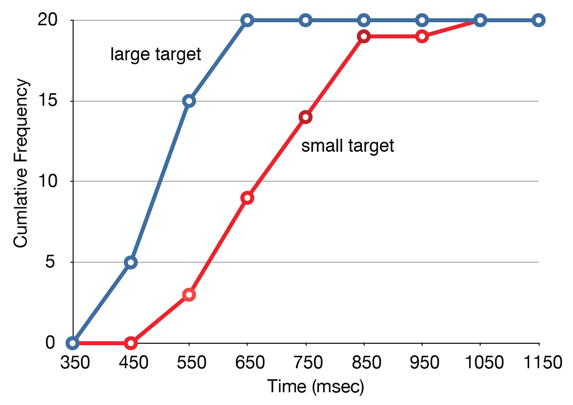
It is also possible to plot two cumulative frequency distributions in the same graph. This is illustrated in Figure \(\PageIndex{4}\) using the same data from the cursor task. The difference in distributions for the two targets is again evident.


