7.5: Standard Normal Distribution
- Page ID
- 2121
Learning Objectives
- State the mean and standard deviation of the standard normal distribution
- Use a \(Z\) table
- Use the normal calculator
- Transform raw data to \(Z\) scores
As discussed in the introductory section, normal distributions do not necessarily have the same means and standard deviations. A normal distribution with a mean of \(0\) and a standard deviation of \(1\) is called a standard normal distribution.
Areas of the normal distribution are often represented by tables of the standard normal distribution. A portion of a table of the standard normal distribution is shown in Table \(\PageIndex{1}\).
| Z | Area below |
|---|---|
| -2.5 | 0.0062 |
| -2.49 | 0.0064 |
| -2.48 | 0.0066 |
| -2.47 | 0.0068 |
| -2.46 | 0.0069 |
| -2.45 | 0.0071 |
| -2.44 | 0.0073 |
| -2.43 | 0.0075 |
| -2.42 | 0.0078 |
| -2.41 | 0.008 |
| -2.4 | 0.0082 |
| -2.39 | 0.0084 |
| -2.38 | 0.0087 |
| -2.37 | 0.0089 |
| -2.36 | 0.0091 |
| -2.35 | 0.0094 |
| -2.34 | 0.0096 |
| -2.33 | 0.0099 |
| -2.32 | 0.0102 |
The first column titled "\(Z\)" contains values of the standard normal distribution; the second column contains the area below \(Z\). Since the distribution has a mean of \(0\) and a standard deviation of \(1\), the \(Z\) column is equal to the number of standard deviations below (or above) the mean. For example, a \(Z\) of \(-2.5\) represents a value \(2.5\) standard deviations below the mean. The area below \(Z\) is \(0.0062\).
The same information can be obtained using the following Java applet. Figure \(\PageIndex{1}\) shows how it can be used to compute the area below a value of \(-2.5\) on the standard normal distribution. Note that the mean is set to \(0\) and the standard deviation is set to \(1\).
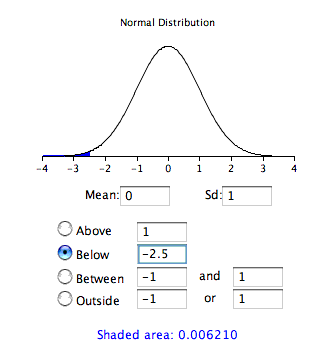
Calculate Areas
A value from any normal distribution can be transformed into its corresponding value on a standard normal distribution using the following formula:
\[Z=\frac{X-\mu }{\sigma }\]
where \(Z\) is the value on the standard normal distribution, \(X\) is the value on the original distribution, \(\mu\) is the mean of the original distribution, and \(\sigma\) is the standard deviation of the original distribution.
Example \(\PageIndex{1}\)
As a simple application, what portion of a normal distribution with a mean of \(50\) and a standard deviation of \(10\) is below \(26\)?
Solution
Applying the formula, we obtain
\[Z = \frac{26 - 50}{10} = -2.4\]
From Table \(\PageIndex{1}\), we can see that \(0.0082\) of the distribution is below \(-2.4\). There is no need to transform to \(Z\) if you use the applet as shown in Figure \(\PageIndex{2}\).
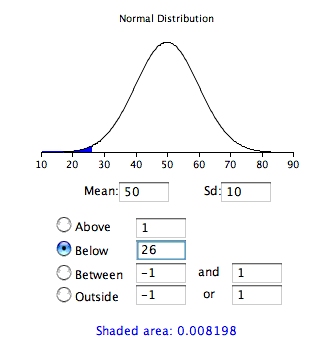
If all the values in a distribution are transformed to \(Z\) scores, then the distribution will have a mean of \(0\) and a standard deviation of \(1\). This process of transforming a distribution to one with a mean of \(0\) and a standard deviation of \(1\) is called standardizing the distribution.


