5.10: Changing the Conditionality and Bayesian Statistics

A trucking company is concerned that some of their drivers may be using amphetamine drugs to stay awake, exposing the company to lawsuits. They hire a testing agency to randomly test drivers. The marketing material for this testing agency claims that 99% of drivers who are using amphetamines will have a positive test result, so the company can be assured that any driver who tests positive will almost certainly be using the amphetamines.

This marketing material presented by the testing agency represents faulty reasoning. The 99% represents the probability that a driver tests positive given the driver is using amphetamines, while the claim was that the probability would be near‐certain that a driver was using amphetamines given the test was positive. The conditionality has been incorrectly switched because in general: \(P(A \mid B) \neq P(B \mid A)\).

To switch the conditionality requires several pieces of information and is often explained in statistics books by using Bayes' Theorem:

If the sample space is the union of mutually events \(\mathrm{A}_{1}, \mathrm{~A}_{2}, \ldots, \mathrm{A}_{n}\), then

\[P\left(A_{i} \mid B\right)=\frac{P\left(A_{i}\right) \times P\left(B \mid A_{i}\right)}{P\left(A_{1}\right) \times P\left(B \mid A_{1}\right)+P\left(A_{2}\right) \times P\left(B \mid A_{2}\right)+\cdots+P\left(A_{n}\right) \times P\left(B \mid A_{n}\right)} \nonumber \]

A more straightforward approach to solving this type of problem is to use techniques that have already been covered in this section:

• First construct a tree diagram.
• Second, create a Contingency Table using a convenient radix (sample size).  
• From the Contingency table it is easy to calculate all conditional probabilities.

Example: Diagnostic testing

10% of prisoners in a Canadian prison are HIV positive. (This is also known in medical research as the incidence rate or prevalence). A test will correctly detect HIV 95% of the time, but will incorrectly “detect” HIV in non‐infected prisoners 15% of the time (false positive). If a randomly selected prisoner tests positive, find the probability the prisoner is HIV+.

Solution

Let A be the event that a prisoner is HIV positive and B the event that a prisoner tests positive. Then A' would be the event that a prisoner is HIV negative and B' would be the event that the prisoner tests negative.

There are four possible outcomes in this probability model:

• True Positive (also known as in medical research as sensitivity) ‐ The prisoner correctly tests positive and is actually HIV positive.
• False Negative ‐ The prisoner incorrectly tests negative and is actually HIV positive.
• False Positive ‐ The prisoner incorrectly tests positive and is actually HIV negative.
• True Negative (also known as in medical research as specificity)  ‐  The prisoner correctly tests negative and is actually is HIV negative.

From the information given, first construct a tree diagram.  

\(P(A) = 0.10 P(A')\) = 1 ‐ 0.10 = 0.90

\(P(B|A)\) = 0.95     \(P(B|A')\) = 0.15     \(P(B'|A)\) = 1 ‐ 0.95 = 0.05     \(P(B'|A')\) = 1 ‐ 0.15 = 0.85

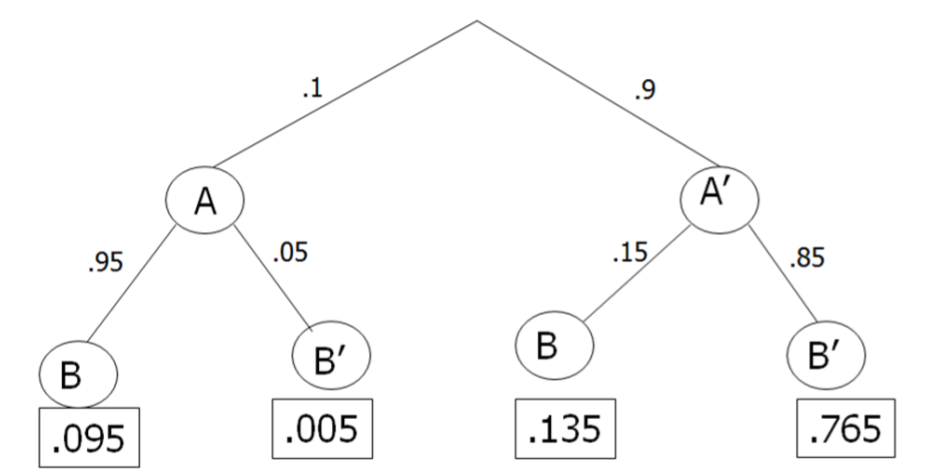
Next, construct a contingency table. It is helpful to choose a convenient radix (sample size) such as 10000 and multiply by each joint probability from the tree diagram:

• Samples in A and B = (.095)(10000) = 950
• Samples in A and B' = (.005)(10000) = 50
• Samples in A' and B = (.135)(10000) = 1350
• Samples in A' and B' = (.765)(10000) = 7650

	HIV+ A	HIV- A'	Total
Test+ B	950	1350	2300
Test- B'	50	7650	7700
Total	1000	9000	10000

To find the probability that a prisoner who tests positive really is HIV positive, find \(P(A|B)\):

\[P(A \mid B)=\dfrac{950}{2300}=0.413 \nonumber \]

So the probability that a prisoner who tests positive really is HIV positive is only 41.3%. This result may seem unusual, but when the incidence rate is lower than the false positive rate, it is more likely that a positive result on a test will be incorrect.

This problem could have also been answered directly, but much less straightforward by using Bayes' Theorem:

\[\begin{aligned}
P(B \mid A) &=\dfrac{P(A) \times P(B \mid A)}{P(A) \times P(B \mid A)+P\left(A^{\prime}\right) \times P\left(B \mid A^{\prime}\right)} \\
&=\dfrac{(0.10)(0.95)}{(0.10)(0.95)+(0.90)(0.85)}\\ &=0.413
\end{aligned} \nonumber \]