5.8: Multiplicative Rule and Tree Diagrams

Last updated
Save as PDF

Page ID: 20884

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Earlier, we learned about the additive rule for finding the joint probability of the Union of two events. There is a corresponding multiplicative rule to find the probability of the Intersection of two events. Using algebra, this rule can calculated directly from the Rule for Conditional Probability.

Multiplicative Rule of Probability

\[P(A \text { and } B)=P(A) \times P(B \mid A) \nonumber \]

\[P(A \text { and } B)=P(B) \times P(A \mid B) \nonumber \]

One useful way to express the Multiplicative Rule is by creating a tree diagram, a simple way to express all possible outcomes in a sequence of events.

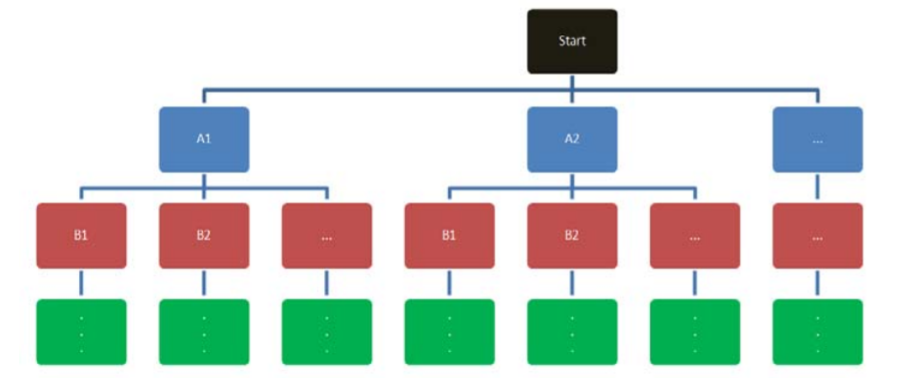
The first level of branches connecting to the start are marginal probabilities, and all lower levels of branches are conditional probabilities. To find the probability of getting to the end of any last branch, multiply the probabilities of all branches that connect back to Start.

Example: Red and green balls

A box contains 4 green balls and 3 red balls. Two balls are drawn, one at a time, without replacement. Make a tree diagram and find the probability of choosing two red balls.

Solution

Let A be the event red on the first Draw and B be the event R]red on second draw. Then in this example A' would be the event green (not red) on the first and B' would be the event green on the second draw.

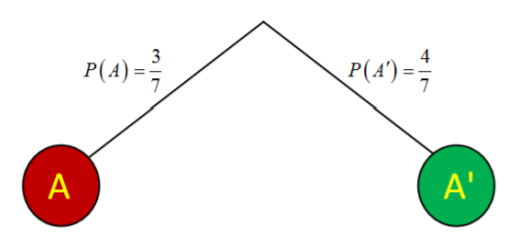
First, make a tree of the first draw and assign probabilities based on the number of balls in the box; 3 out of 7 are red and 4 out of 7 are green.

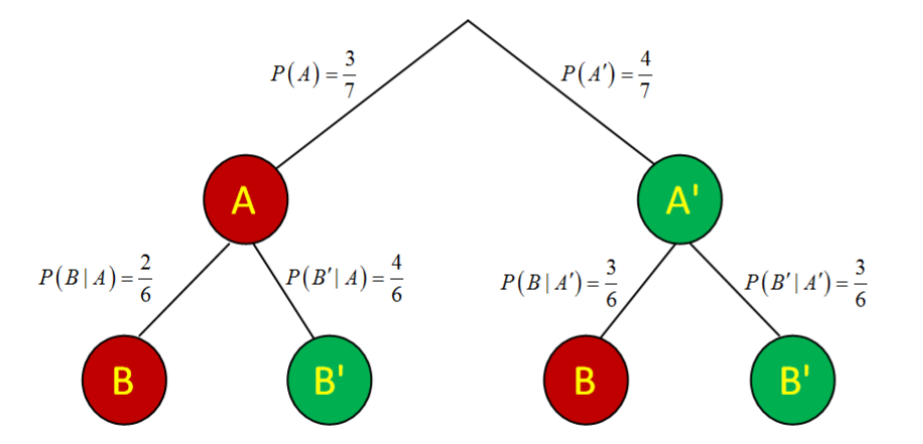
Next, conduct the second draw, assuming the ball chosen on the first draw is gone. For example, if the first draw was red, the chance of getting another red is 2 out of 6, since there are 2 remaining reds and 4 remaining greens. However, if the first draw was green, the chance of getting red is 3 out of 6.

Finally, use the multiplicative rule and multiply down the branch to get all joint probabilities. If you have constructed the tree diagram correctly, all of these probabilities must add to 1.

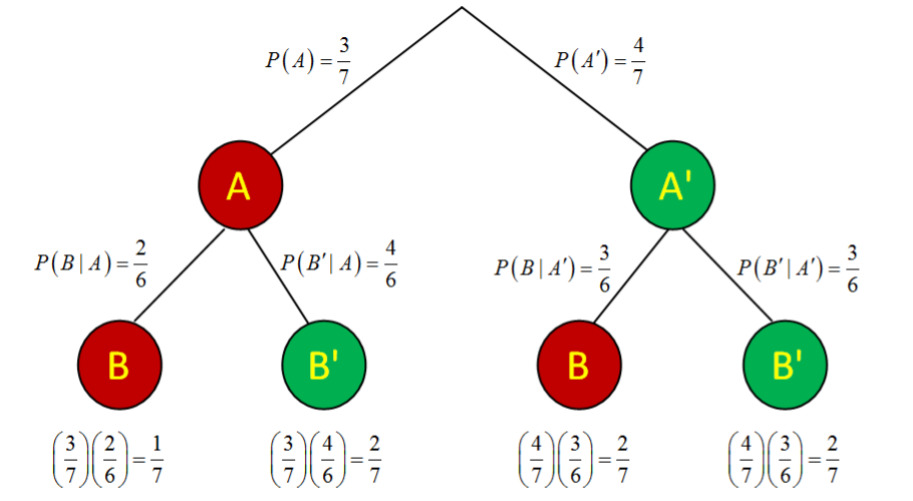
The probability of getting 2 red balls is 1/7 or approximately 0.143

Example: Circuit switches

A Circuit has three linear switches. If at least two of the switches function, the Circuit will succeed. Each switch has a 10% failure rate if all are operating, and a 20% failure rate if one switch has already failed. Construct a tree diagram and find the probability that the circuit will succeed.

Solution

Event A = first switch succeeds Event A' = first switch fails

Event B = second switch succeeds Event B' = second switch fails

Event C = third switch succeeds Event C' = third switch fails

P(2 or more successes) = 0.81 + 0.072 + 0.064 = 0.946

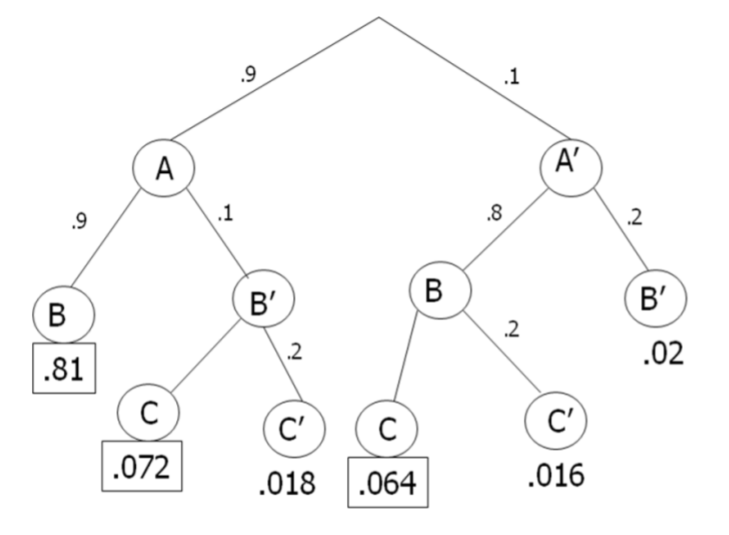
The switch has a 94.6% chance of succeeding. Notice that we did not need a tie‐breaking third branch for the cases of the first 2 switches succeeding, or the first 2 switches failing.