5.6: Conditional Probability

Last updated
Save as PDF

Page ID: 20882

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Conditional Probability means the probability of an event A occurring given that another event B has already occurred. This probability is written as \(P(A|B)\) which is read as \(P(A \text{ given } B)\).

Example: 2016 presidential election

In the 2016 United States presidential election, Donald Trump received 46% of the total vote, Hillary Clinton received 48%, and other candidates received 6%. (Note: although Clinton received about 3 million more votes than Trump, the Electoral College determined the actual winner to be Trump).

CNN conducted exit polls to determine how people voted based on demographic statistics, such as gender.⁶⁴ These exit polls showed that 53% of the voters were female and 47% of the voters were male. These two values are examples of marginal probabilities.

The polls also showed that Donald Trump received 41% of the female vote and 52% of the male vote. These two values are examples of conditional probability, in which the condition is knowing the gender of the voter.

Solution

Events	Marginal Probabilities	Conditional Probabilities
T = Voter chooses Trump	\(P(T)=0.46\)	\(P(T\|F) = 0.41\)
F = Voter is Female	\(P(F) = 0.53\)	\(P(T\|M) = 0.52\)
M = Voter is Male	\(P(M) = 0.47\)

In calculating the probability of A given B, we only need to consider the elements of Event B instead of the entire sample space.

Example: Student courses

Let us revisit the example of students taking Math and History. Suppose we wanted to calculate the probability that a student who is taking math is also taking history.

Solution

In this case we only need to consider the 40 students taking math as the sample space and the 10 students taking both math and history as the conditional event occurring.

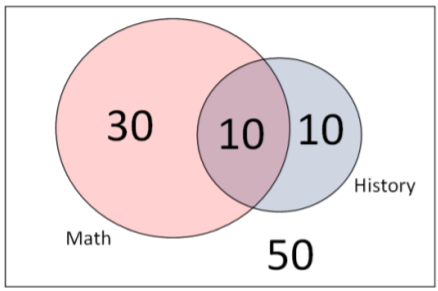
\(P(\text { History })=20 / 100=0.20\)

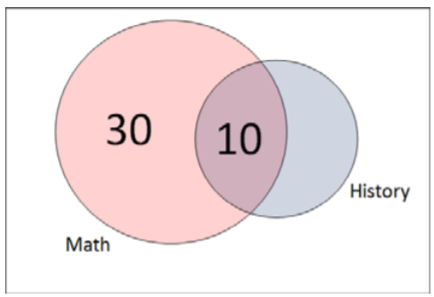
\(P(\text { History } \mid \text { Math })=10 / 40=0.25\)

In this example, we used classical counting probability rules, but conditional probability can be calculated directly using known marginal and conditional probabilities.

Rules for Conditional Probability

\[P(A \mid B)=\dfrac{P(A \text { and } B)}{P(B)} \nonumber \]

\[P(B \mid A)=\dfrac{P(A \text { and } B)}{P(A)} \nonumber \]

Example: Cell phone carrier

Of all cell phone users in the US, 15% have a smart phone with AT&T. 25% of all cell phone users use AT&T. Given a selected cell phone user has AT&T, find the probability the user also has a smart phone.

Solution

Let A = AT&T subscriber. Let B = Smart Phone User

\(P(A)=0.25 \quad P(A \text { and } B)=0.15\)

\(P(A \mid B)=\dfrac{0.15}{0.25}=0.60\)

This means 60% of all AT&T subscribers have smart phones.