1.2: Probability Distribution
- Page ID
- 2870
Once we have organized and summarized your sample data, the next step is to identify the underlying distribution of our random variable. Computing probabilities for continuous random variables are complicated by the fact that there are an infinite number of possible values that our random variable can take on, so the probability of observing a particular value for a random variable is zero. Therefore, to find the probabilities associated with a continuous random variable, we use a probability density function (PDF).
A PDF is an equation used to find probabilities for continuous random variables. The PDF must satisfy the following two rules:
- The area under the curve must equal one (over all possible values of the random variable).
- The probabilities must be equal to or greater than zero for all possible values of the random variable.
The area under the curve of the probability density function over some interval represents the probability of observing those values of the random variable in that interval.
The Normal Distribution
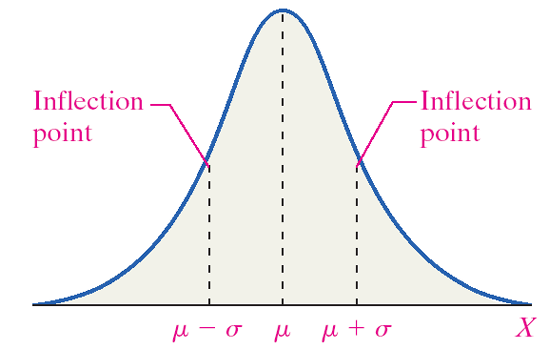
Many continuous random variables have a bell-shaped or somewhat symmetric distribution. This is a normal distribution. In other words, the probability distribution of its relative frequency histogram follows a normal curve. The curve is bell-shaped, symmetric about the mean, and defined by µ and σ (the mean and standard deviation).
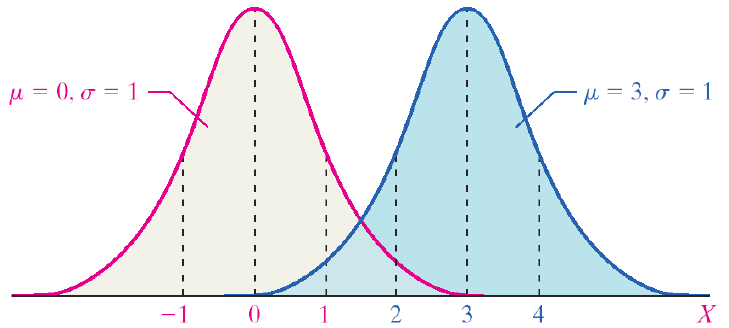
There are normal curves for every combination of µ and σ. The mean (µ) shifts the curve to the left or right. The standard deviation (σ) alters the spread of the curve. The first pair of curves have different means but the same standard deviation. The second pair of curves share the same mean (µ) but have different standard deviations. The pink curve has a smaller standard deviation. It is narrower and taller, and the probability is spread over a smaller range of values. The blue curve has a larger standard deviation. The curve is flatter and the tails are thicker. The probability is spread over a larger range of values.

Properties of the normal curve:
- The mean is the center of this distribution and the highest point.
- The curve is symmetric about the mean. (The area to the left of the mean equals the area to the right of the mean.)
- The total area under the curve is equal to one.
- As x increases and decreases, the curve goes to zero but never touches.
- The PDF of a normal curve is \[ y= \frac {1}{\sqrt {2\pi} \sigma} e^{\frac {-(x-\mu)^2}{2\sigma^2}}\]
- A normal curve can be used to estimate probabilities.
- A normal curve can be used to estimate proportions of a population that have certain x-values.
The Standard Normal Distribution
There are millions of possible combinations of means and standard deviations for continuous random variables. Finding probabilities associated with these variables would require us to integrate the PDF over the range of values we are interested in. To avoid this, we can rely on the standard normal distribution. The standard normal distribution is a special normal distribution with a µ = 0 and σ = 1. We can use the Z-score to standardize any normal random variable, converting the x-values to Z-scores, thus allowing us to use probabilities from the standard normal table. So how do we find area under the curve associated with a Z-score?
Standard Normal Table
- The standard normal table gives probabilities associated with specific Z-scores.
- The table we use is cumulative from the left.
- The negative side is for all Z-scores less than zero (all values less than the mean).
- The positive side is for all Z-scores greater than zero (all values greater than the mean).
- Not all standard normal tables work the same way.
What is the area associated with the Z-score 1.62?
|
|
.00 |
.01 |
.02 |
.03 |
.04 |
.05 |
.06 |
.07 |
.08 |
.09 |
|
0.0 |
0.5000 |
0.5040 |
0.5080 |
0.5120 |
0.5160 |
0.5199 |
0.5239 |
0.5279 |
0.5319 |
0.5359 |
|
0.1 |
0.5398 |
0.5438 |
0.5478 |
0.5517 |
0.5557 |
0.5596 |
0.5636 |
0.5675 |
0.5714 |
0.5753 |
|
0.2 |
0.5793 |
0.5832 |
0.5871 |
0.5910 |
0.5948 |
0.5987 |
0.6026 |
0.6064 |
0.6103 |
0.6141 |
|
1.5 |
0.9332 |
0.9345 |
0.9357 |
0.9370 |
0.9382 |
0.9394 |
0.9406 |
0.9418 |
0.9429 |
0.9441 |
|
1.6 |
0.9452 |
0.9463 |
0.9474 |
0.9484 |
0.9495 |
0.9595 |
0.9515 |
0.9525 |
0.9535 |
0.9545 |
|
1.7 |
0.9554 |
0.9564 |
0.9573 |
0.9582 |
0.9591 |
0.9599 |
0.9608 |
0.9616 |
0.9625 |
0.9633 |

Answer
The area is 0.9474.
Reading the Standard Normal Table
- Read down the Z-column to get the first part of the Z-score (1.6).
- Read across the top row to get the second decimal place in the Z-score (0.02).
- The intersection of this row and column gives the area under the curve to the left of the Z-score.
Finding Z-scores for a Given Area
- What if we have an area and we want to find the Z-score associated with that area?
- Instead of Z-score → area, we want area → Z-score.
- We can use the standard normal table to find the area in the body of values and read backwards to find the associated Z-score.
- Using the table, search the probabilities to find an area that is closest to the probability you are interested in.
To find a Z-score for which the area to the right is 5%:
Since the table is cumulative from the left, you must use the complement of 5%.
\[1.000 – 0.05 = 0.9500 \nonumber \]

- Find the Z-score for the area of 0.9500.
- Look at the probabilities and find a value as close to 0.9500 as possible.
The standard normal table
-
 z
z.00
.01
.02
.03
.04
.05
.06
.07
.08
.09
0.0
0.5000
0.5040
0.5080
0.5120
0.5160
0.5199
0.5239
0.5279
0.5319
0.5359
0.1
0.5398
0.5438
0.5478
0.5517
0.5557
0.5596
0.5636
0.5675
0.5714
0.5753
0.2
0.5793
0.5832
0.5871
0.5910
0.5948
0.5987
0.6026
0.6064
0.6103
0.6141
1.5
0.9332
0.9345
0.9357
0.9370
0.9382
0.9394
0.9406
0.9418
0.9429
0.9441
1.6
0.9452
0.9463
0.9474
0.9484
0.9495
0.9595
0.9515
0.9525
0.9535
0.9545
1.7
0.9554
0.9564
0.9573
0.9582
0.9591
0.9599
0.9608
0.9616
0.9625
0.9633
Answer
The Z-score for the 95th percentile is 1.64.
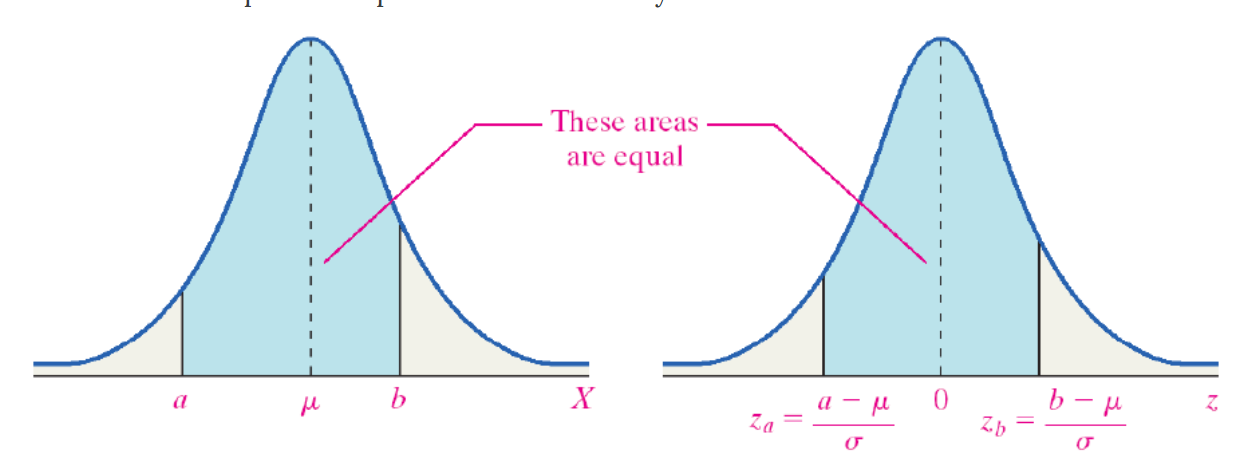
Area in between Two Z-scores
To find Z-scores that limit the middle 95%:
- The middle 95% has 2.5% on the right and 2.5% on the left.
- Use the symmetry of the curve.

Solution
- Look at your standard normal table. Since the table is cumulative from the left, it is easier to find the area to the left first.
- Find the area of 0.025 on the negative side of the table.
- The Z-score for the area to the left is -1.96.
- Since the curve is symmetric, the Z-score for the area to the right is 1.96.
Common Z-scores
There are many commonly used Z-scores:
- \(Z_{.05}\) = 1.645 and the area between -1.645 and 1.645 is 90%
- \(Z_{.025}\) = 1.96 and the area between -1.96 and 1.96 is 95%
- \(Z_{.005}\) = 2.575 and the area between -2.575 and 2.575 is 99%
Applications of the Normal Distribution
Typically, our normally distributed data do not have μ = 0 and σ = 1, but we can relate any normal distribution to the standard normal distributions using the Z-score. We can transform values of x to values of z.
\[z=\frac {x-\mu}{\sigma}\]
For example, if a normally distributed random variable has a μ = 6 and σ = 2, then a value of x = 7 corresponds to a Z-score of 0.5.
\[Z=\frac{7-6}{2}=0.5\]
This tells you that 7 is one-half a standard deviation above its mean. We can use this relationship to find probabilities for any normal random variable.
To find the area for values of X, a normal random variable, draw a picture of the area of interest, convert the x-values to Z-scores using the Z-score and then use the standard normal table to find areas to the left, to the right, or in between.
\[z=\frac {x-\mu}{\sigma}\]
Adult deer population weights are normally distributed with µ = 110 lb. and σ = 29.7 lb. As a biologist you determine that a weight less than 82 lb. is unhealthy and you want to know what proportion of your population is unhealthy.
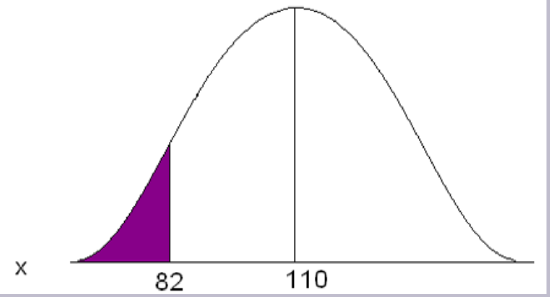
Convert 82 to a Z-score
\[z=\frac{82-110}{29.7} = -0.94 \nonumber \]
The x value of 82 is 0.94 standard deviations below the mean.
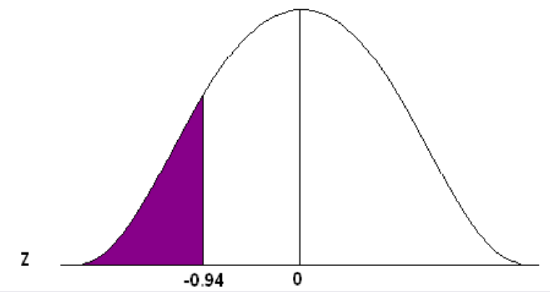
Go to the standard normal table (negative side) and find the area associated with a Z-score of -0.94.
This is an “area to the left” problem so you can read directly from the table to get the probability.
\[P(x<82) = 0.1736 \nonumber \]
Approximately 17.36% of the population of adult deer is underweight, OR one deer chosen at random will have a 17.36% chance of weighing less than 82 lb.
Statistics from the Midwest Regional Climate Center indicate that Jones City, which has a large wildlife refuge, gets an average of 36.7 in. of rain each year with a standard deviation of 5.1 in. The amount of rain is normally distributed. During what percent of the years does Jones City get more than 40 in. of rain?
\[P(x > 40) \nonumber \]
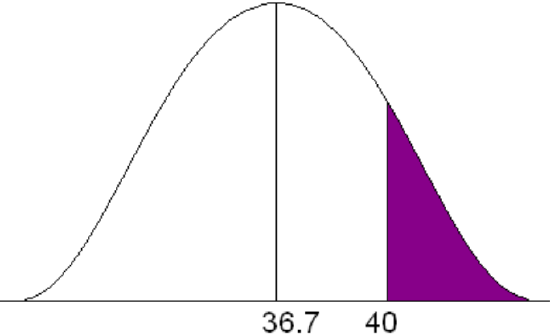
Solution
\[z=\frac {40-36.7}{5.1}=0.65 \nonumber \]
\[ P(x>40) = (1-0.7422) = 0.2578 \nonumber \]
For approximately 25.78% of the years, Jones City will get more than 40 in. of rain.
Assessing Normality
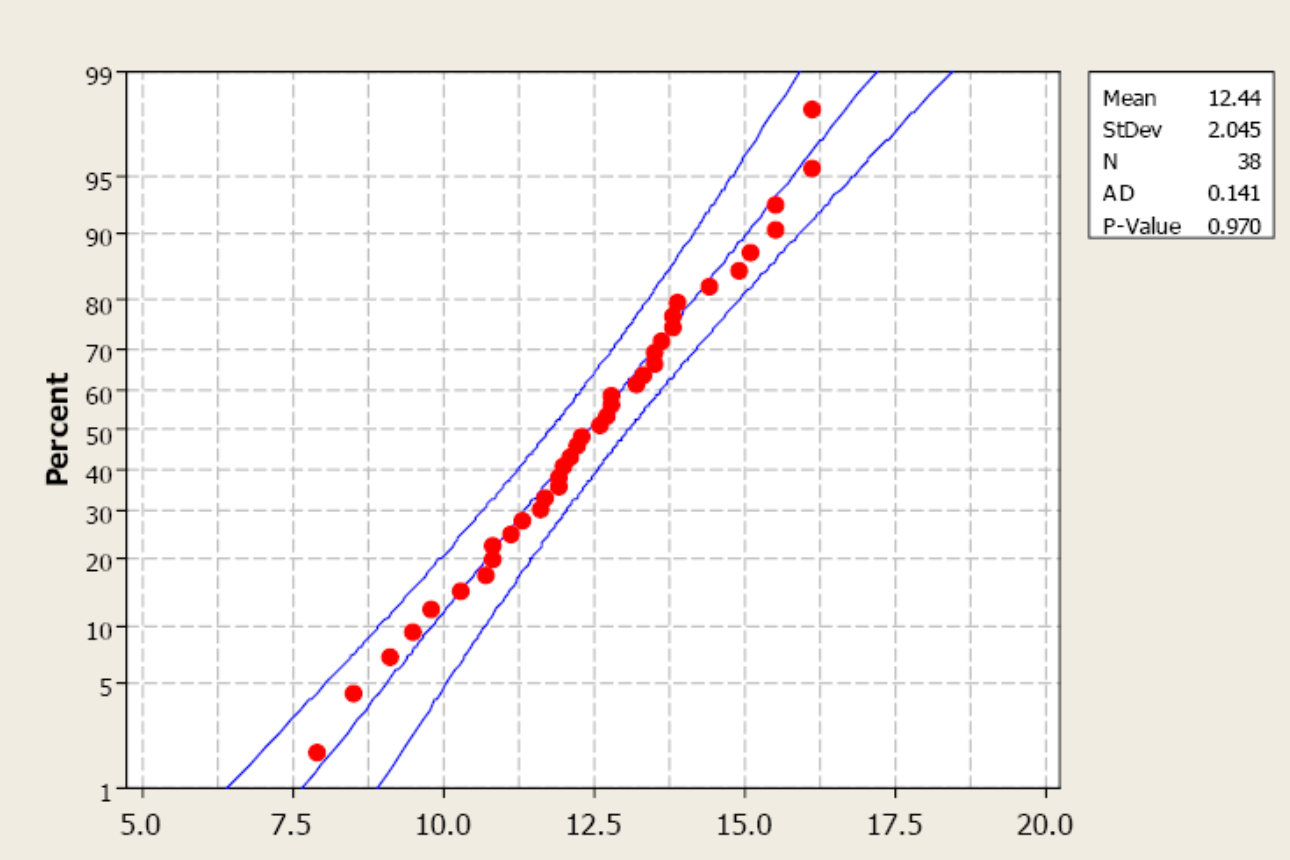
If the distribution is unknown and the sample size is not greater than 30 (Central Limit Theorem), we have to assess the assumption of normality. Our primary method is the normal probability plot. This plot graphs the observed data, ranked in ascending order, against the “expected” Z-score of that rank. If the sample data were taken from a normally distributed random variable, then the plot would be approximately linear.
Examine the following probability plot. The center line is the relationship we would expect to see if the data were drawn from a perfectly normal distribution. Notice how the observed data (red dots) loosely follow this linear relationship. Minitab also computes an Anderson-Darling test to assess normality. The null hypothesis for this test is that the sample data have been drawn from a normally distributed population. A p-value greater than 0.05 supports the assumption of normality.
Compare the histogram and the normal probability plot in this next example. The histogram indicates a skewed right distribution.
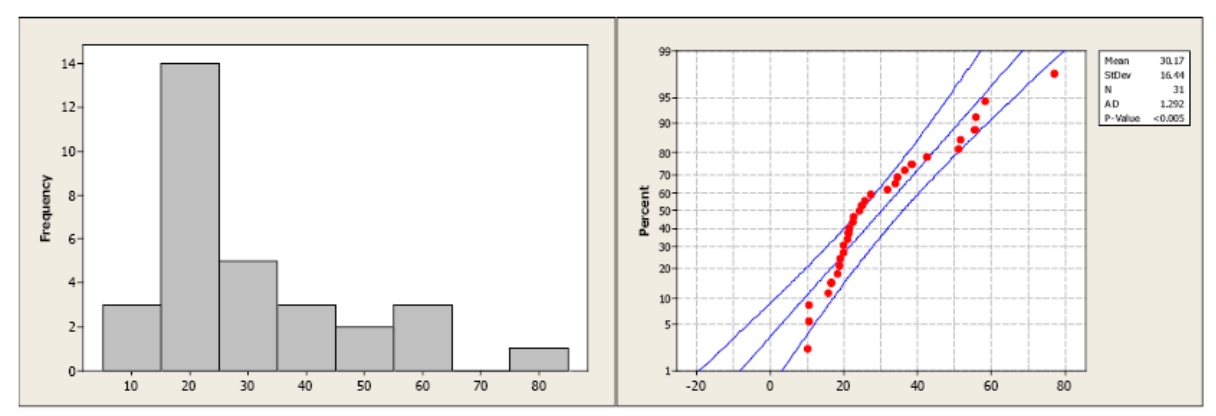
The observed data do not follow a linear pattern and the p-value for the A-D test is less than 0.005 indicating a non-normal population distribution.
Normality cannot be assumed. You must always verify this assumption. Remember, the probabilities we are finding come from the standard NORMAL table. If our data are NOT normally distributed, then these probabilities DO NOT APPLY.
- Do you know if the population is normally distributed?
- Do you have a large enough sample size (n≥30)? Remember the Central Limit Theorem?
- Did you construct a normal probability plot?


