14.7: Rcmdr Multiway ANOVA

Introduction

We have been talking about the two-way randomized, balanced, replicated design. Here, we take you step by step through use of R to conduct the multiway ANOVA.

R code: Multiway ANOVA

Rcmdr: Statistics → Means → Multiway ANOVA… we will review this as Option 1

or

Rcmdr: Statistics → Fit Models → Linear model… we will review this as Option 2

In either case, as a reminder, your data set must be a stacked worksheet, like the data in this table.

Table \(\PageIndex{1}\). Data set, example.14.7^†

Diet	Population	Response
A	1	4
A	1	6
A	1	5
A	2	5
A	2	8
A	2	9
B	1	12
B	1	15
B	1	11
B	2	5
B	2	7
B	2	8

Option 1

Your first option is to use the ANOVA menus via “Means.” This is a perfectly good way to handle a standard two-way, fully-crossed, fixed effects model. However, other designs will not run with this command and R will return a report of errors for ANOVA models that do not conform to the replicated, balanced, crossed design.

Rcmdr: Statistics → Means → Multiway Analysis of variance …

Factors: highlight “Diet” AND “Population”

Response variable: pick one (in this window, all we see is “Response”)

Figure \(\PageIndex{1}\): Multi-Way Analysis of Variance popup in R Commander.

^†Note:

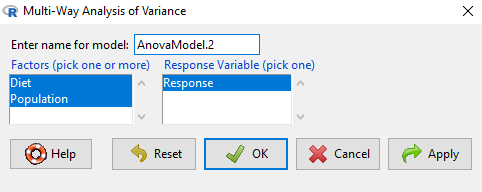
Don’t forget to convert numeric Population to factor

Interpret the output

AnovaModel.2 <- (lm(Response ~ Diet*Population, data=example.14.7))

Anova(AnovaModel.2)
 
Anova Table (Type II tests)
Response: Response
                  Sum Sq    Df    F value      Pr(>F) 
Diet              36.750     1    12.2500    0.008079 **
Population        10.083     1     3.3611    0.104104 
Diet:Population   52.083     1    17.3611    0.003136 **
Residuals         24.000     8
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
tapply(example.14.7 Response, list(Diet=example.14.7 Diet, 
+ Population=example.14.7 Population), mean, na.rm=TRUE) # means
Population
Diet 1 2
A 5.00000 7.333333
B 12.66667 6.666667

tapply(example.14.7 Response, list(Diet=example.14.7 Diet, 
+ Population=example.14.7 Population), sd, na.rm=TRUE) # std. deviations
Population
Diet 1 2
A 1.000000 2.081666
B 2.081666 1.527525

tapply(example.14.7 Response, list(Diet=example.14.71 Diet, 
+ Population=example.14.7 Population), function(x) sum(!is.na(x))) # counts
Population
Diet 1 2
A 3 3
B 3 3

End R output

Summary of multi-way ANOVA command

The multi-way ANOVA command returns our ANOVA table plus the adjusted means, along with standard deviations and number of observations (counts). The adjusted means would then be good to put into a chart to present group comparisons following adjustments from the effects of levels within groups.

Rcmdr: Models → Graphs → Predictor effect plots …

Here’s the chart (hint: \(\pm SEM = \frac{SD}{\sqrt{count}}\))

Figure \(\PageIndex{2}\): Plots of the predictor effects of each factor.

Option 2

A more general approach is to use the General linear model. This approach can handle the standard 2-way fixed effects ANOVA (above), but any other model as well. The model is Response ~ Diet*Population.

Rcmdr: Statistics → Fit Models → Linear model…

Figure \(\PageIndex{3}\): Linear Model screenshot in R Commander with model formula input.

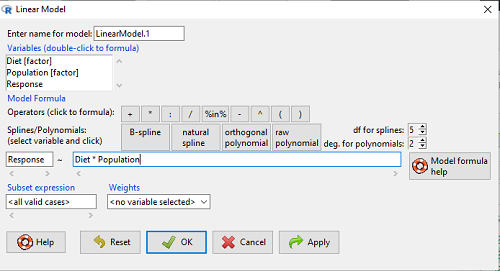
Interpret the output

LinearModel.1 <- lm(Response ~ Diet * Population, data=example.14.7)

summary(LinearModel.1)

Call:
lm(formula = Response ~ Diet * Population, data = example.14.7)

Residuals:
Min 1Q Median 3Q Max 
-2.3333 -1.1667 0.1667 1.0833 2.3333 

Coefficients:
                        Estimate    Std. Error ..t value .  Pr(>|t|) 
(Intercept) .              5.000         1.000 .   5.000    .0.00105 ** 
Diet[T.B] .                7.667       ..1.414 .   5.421    .0.00063 ***
Population[T.2]           .2.333       ..1.414 .   1.650    .0.13757 
Diet[T.B]:Population[T.2] -8.333       ..2.000    -4.167    .0.00314 ** 
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

Residual standard error: 1.732 on 8 degrees of freedom
Multiple R-squared: 0.8047, Adjusted R-squared: 0.7315 
F-statistic: 10.99 on 3 and 8 DF, p-value: 0.003285 

End R output

Lots to sort through, so let’s begin with what is in common between the two approaches in Rcmdr, the Multi-way ANOVA command versus the linear model command.

Compare the two outputs

As a direct output, the linear model option does not provide an ANOVA summary table. Instead of our ANOVA table, the linear model returns estimates of coefficients along with \(t\)-test results for each coefficient of the model from the lm() command output

Recall that we can get ANOVA tables through the following R commands via Rcmdr.

Rcmdr: Models → Hypothesis tests → ANOVA Table.

Let’s do so for this linear model (accept the default for type of tests = “Type II”).

And the output is

Anova(LinearModel.1, type="II")
Anova Table (Type II tests)

Response: Response
                Sum Sq Df F value   Pr(>F)   
Diet            36.750  1 12.2500 0.008079 **
Population      10.083  1  3.3611 0.104104   
Diet:Population 52.083  1 17.3611 0.003136 **
Residuals       24.000  8                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

End R output

Now we’re in business, and, using the lm() function, we have the estimates for each model coefficient plus our ANOVA table.

Both methods give the same answer! Of course. Which to choose, Option 1 or Option 2? Use the lm() option: it is more flexible and covers more designs than the multiway ANOVA, which is strictly for the crossed fully replicated design.

---

Questions

1. Write out the two-way model described for the data in Table \(\PageIndex{1}\).
2. Write the null hypotheses and provide a summary of the statistical significance of the model.