6.8: Moments
- Page ID
- 45071
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Moments are used to describe the shape of a distribution. For those of you who remember your calculus, moments were discussed as a method to find the center of mass, or balancing point (Herman and Strang 2018). For distributions, the center and shape moments follow from the expected value of the probability function.
Expected value of a statistic is calculated by multiplying the likelihood of each possible outcome in a sample space by that outcome, then adding up all of those product values. From probability theory it is the weighted average of the outcomes of a random variable. A simpler way to think of the expected value is that if one were to guess the height of a person, the expected value is the average height of the population from which the person would be selected.
Four moments apply for describing the shape of a distribution. The 1st moment describes the middle, the 2nd describes the spread from the middle, the 3rd describes symmetry about the middle, and the 4th describes the shape, whether peaked and sharp, or leptokurtic, or broad and flattened, or platykurtic.
Equations for the moments
Over the years, several equations have been proposed to estimate skewness and kurtosis. The above formulas are just one example from the list (Joanes and Gill 1998).
Pearson’s standardized moments: \[\frac{\mu_{n}}{\sigma^{n}} \equiv \frac{E[X - \mu]^{n}}{\sigma^{2}} \nonumber\]
where \(E\) is the expected value of the random variable. The expected value concept follows from rules of probability — basically, the average of a large number, \(n\), of \(X\).
Four moments can be used to describe the shape of a distribution.
1st moment, \(μ\) (mean): population mean, 3.2 – Measures of Central Tendency
2nd moment, \(\sigma^{2}\) (variance): population variance, 3.3 – Measures of dispersion
3rd moment, \(\bar{\mu}_{3}\) (skew): \[\frac{\mu_{3}}{\sigma^{3}} = \frac{\sqrt{n(n-1)}}{n-2} \left[\frac{\dfrac{1}{n} \displaystyle\sum (X-\mu)^{3}}{\left( \dfrac{1}{n} \displaystyle\sum (X-\mu)^{2} \right)^{\frac{3}{2}}}\right] \nonumber\]
4th moment, \(\bar{\mu}_{4}\) (kurtosis): \[\frac{\mu_{4}}{\sigma^{4}} = 3 \sigma^{4} = \frac{\mu_{4}}{\sigma_{2}^{2}} - 3 \nonumber\]
Estimating moments in R and R Commander
In R Commander, we select Statistics → Summaries → Numerical summaries…, which brings up a popup menu. First, select the variable, in this case Minutes, from the Data tab (not shown). Next, click on Statistics tab to choose options (Fig. \(\PageIndex{2}\)).

For estimates of the moments, check Mean, Standard Deviation, Skewness, and Kurtosis. Note that Rcmdr gives you the choice among three different Types of skewness and kurtosis. Type 1 include the equations provided on this page, corresponding to definitions dating back to the 1940s. Type 2 is the default and corresponds to equations used by other professional statistics package (SAS, SPSS). For large sample size, the different types will tend to agree. Caution applies to smaller data sets — the different types may disagree (Joanes and Gill 1998).
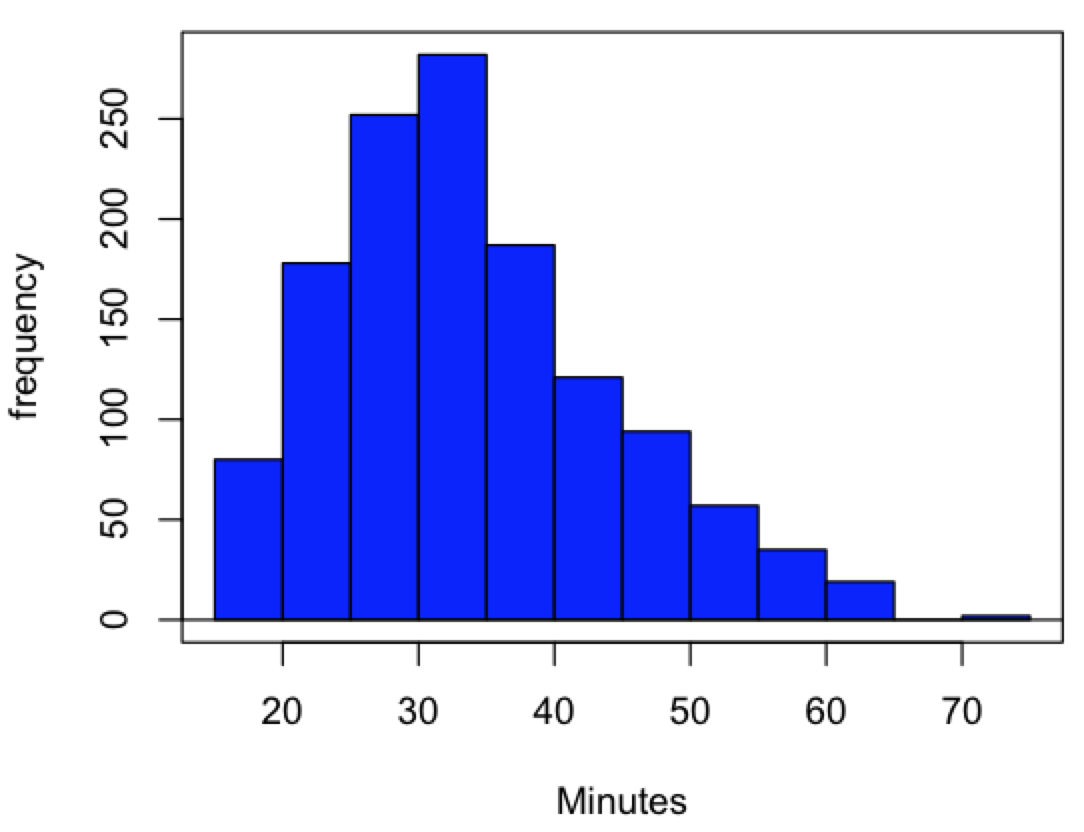
Large sample size, n = 1307
Type 1
mean sd skewness kurtosis n 34.42999 10.31437 0.6159258 -0.01593882 1307
Type 2
mean sd skewness kurtosis n 34.42999 10.31437 0.6166337 -0.01139521 1307
Type 3
mean sd skewness kurtosis n 34.42999 10.31437 0.615219 -0.02050335 1307
Small sample size
To test the claim about sample size and the moment statistics, draw a random sample of 30 from the larger data set. Sample without replacement:
sample.banana <- data.frame(sample(banana5K$Minutes, 30, replace = FALSE))
I forgot to specify a new variable name, so R used the whole command as the variable name. I could go back and fix my function call, or simply rename the variable as follows:
names(sample.banana)[c(1)] <- c("Minutes")
The random sample yielded a distribution (Fig. \(\PageIndex{3}\)).

Repeat Numerical summaries on small data set, n = 30
Type 1:
mean sd skewness kurtosis n 33.16667 10.00373 0.5538637 0.5024438 30
Type 2:
mean sd skewness kurtosis n 33.16667 10.00373 0.5834511 0.8276415 30
Type 3:
mean sd skewness kurtosis n 33.16667 10.00373 0.5264025 0.2728392 30
Conclusion: We can compare consistency of the estimators by calculating coefficient of variation. The three types of skewness estimators differed by only 1% and 5% for large and small sample size, respectively. In contrast, the three types of kurtosis estimators differed by 29% and 52% for large and small sample size, respectively.
Questions
1. Explore the consistency of skewness and kurtosis estimates by calculating and comparing coefficient of variation estimates. R Commander provide a nice way to draw randomly from various defined distributions. Draw two data sets of 15 (small) and 1000 (large), from the chi-square distribution (1 degree of freedom) and a minimum of one other continuous distribution.
Example, draw random sample of 1000 from chi-square distribution. Rcmdr: Distributions → Continuous distributions → Chi-squared distribution → Sample from chi-squared distribution…
Enter name for the variable, enter degrees of freedom (e.g., 1), number of samples (e.g., 1000), and number of observations (variables, columns). Leave Sample means checked under data sets.

This results in a new data set. Get “moments” from Numerical summaries and calculate coefficient of variations. Which moments have the most consistency regardless of the kind of distribution.
2. Make histograms for each of your created data sets. Describe what you see about the shape of the plotted distributions.


