6.6: Continuous distributions

Law of Large Numbers and Central Limit Theorem

Imagine we’ve collected (sampled) data from a population and now want to summarize the data sample. How do we proceed? A good starting point is to plot the data in a histogram and note the shape of the sample distribution. Not to get too far ahead of ourselves here, but much of the classical inferential statistics demands that we are able to assume that the sampled values come from a certain kind of distribution called the normal, or Gaussian distribution.

Consider a random sample drawn from a normally distributed population of the following series of graphs, Figures \(\PageIndex{1 – 4}\):

Figure \(\PageIndex{1}\): Sample size = 20, drawn from population with known \(\mu = 0\) and \(\sigma = 1\).

Figure \(\PageIndex{2}\): Sample size = 100, also drawn from population with known \(\mu = 0\) and \(\sigma = 1\).

Figure \(\PageIndex{3}\): Sample size = 1000, once again drawn from population with known \(\mu = 0\) and \(\sigma = 1\).

Figure \(\PageIndex{4}\): And lastly, sample size = 1 million also drawn from population with known \(\mu = 0\) and \(\sigma = 1\).

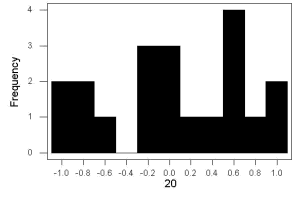
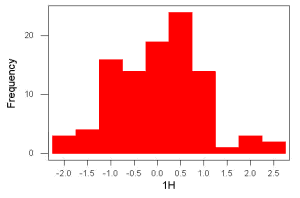
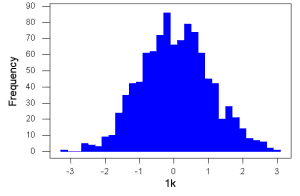
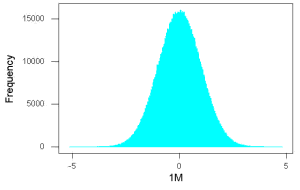
These graphs illustrate a fundamental point in statistics: for many kinds of measurements in biology, the more data you sample, the more likely the data will approach a normal distribution. This series of simulations was a quick and dirty “proof” of the Central Limit Theorem, which is one of the two fundamental theorems of probability, the other being that of Law of Large Numbers (i.e., large-sample statistics). Basically the CLT says that for a large number of random samples, the sample mean will approach the population mean, \(\mu\), and the sample variance will approach the population variance \(\sigma^{2}\); the distribution of the large sample will converge on the normal distribution.

As the sample size gets bigger and bigger, the resulting sample means and standard deviations get closer and closer to the true value (remember — I TOLD the program to grab numbers from the Z distribution with a mean of zero and standard deviation of zero), obeying the Law of Large Numbers.

Simulation

I used the computer to generate sample data from a population. This process is called a simulation. R can make new data sets by sampling from known populations with specified distribution properties that we determine in advance — a very powerful tool — a technique used for many kinds of statistics (e.g., Monte Carlo methods, bootstrapping, etc., see Chapter 19).

Note:

How I got the data. All of these data are from a simulation where I asked told R, “grab random numbers from an infinitely large population, with mean = 0 and standard deviation = 1.”

1. The first graph is for a sample of 20 points;
2. the second for 100;
3. the third for 1,000;
4. and lastly, 1 million points.

To generate a sample from a normal population, in Rcmdr call the menu by selecting:

Rcmdr: Distributions → Continuous distributions → Normal distribution → Sample from normal distribution…

Figure \(\PageIndex{5}\): Screenshot of the Rcmdr menu to sample from a normal distribution.

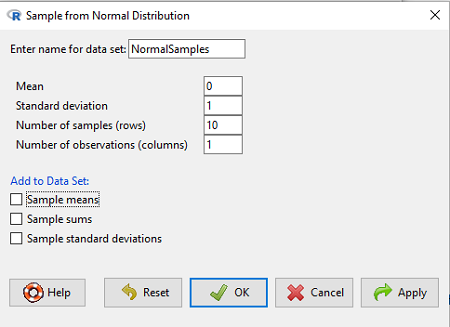
The menu pops up. I entered Mean \((\mu) = 0\) and Standard deviation \((\sigma) = 1\), number of samples = 10, and unchecked all boxes under the “add to data set.” I left the object name as “NormalSamples” but you can, of course, change it as needed. R code derived from these requests were

normalityTest(~obs, test="shapiro.test", data=NormalSamples)
NormalSamples <- as.data.frame(matrix(rnorm(10*1, mean=0, sd=1), ncol=1))
rownames(NormalSamples) <- paste("sample", 1:10, sep="")
colnames(NormalSamples) <- "obs"

This results in a new data.frame called NormalSamples with a single variable called obs.

Note:

About pseudorandom number generators, PRNG. An algorithm is used for creating a sequence of numbers that are like random numbers. We say “like” or “pseudo” random numbers because the algorithm requires a starting number called the seed, rather than a truly random process, i.e., a source of entropy outside of the computer. The default PRNG algorithm in base R is Mersenne Twister (Wikipedia), though there are many others included in base R (bring up the help menu by typing ?RNGkind at the prompt), as well as other packages, like random, which can be used to generate truly random numbers (source of entropy is “atmospheric noise,” per citation in the package, see also random.org).

rnorm() was the function used to sample from a normal distribution. If you run the function over and over again (e.g., use a for loop), each time you will get different samples. For example, results from three runs

for (i in 1:3){
print(rnorm(5))
}
[1] -0.4221672 -1.4317800 -1.8310352 0.4181184 -1.1596058
[1] -0.2034944 1.1809083 1.5925296 -2.0763677 1.6982357
[1] -1.0967218 -0.3205041 -1.7513838 -0.3335311 -1.8808454

However, if you set the seed to the same number before calling rnorm, you’ll get the same sampled numbers.

for (i in 1:3){
set.seed(1) 
print(rnorm(5))
}
[1] -0.6264538 0.1836433 -0.8356286 1.5952808 0.3295078
[1] -0.6264538 0.1836433 -0.8356286 1.5952808 0.3295078
[1] -0.6264538 0.1836433 -0.8356286 1.5952808 0.3295078

The seed number can be any number; it does not have to equal 1.

After creating a sample of numbers drawn from the normal distribution, make a histogram, Rcmdr: Graphs → Histogram… (see Chapter 4.2).

The normal distribution

More on the importance of normal curves in a moment. Sometimes people call these “bell-shaped” curves. You may also see such distributions referred to as Gaussian Distributions, but the normal curve is but one of many Gaussian-type distributions. Moreover, not all “bell-shaped” curves are NORMAL. For a distribution to be “normally distributed” it must follow a specific formula. \[Y_{i} = \frac{1}{\sigma \sqrt{2 \pi}} \cdot e^{\frac{-\left(X_{i} - \mu\right)^{2}}{2 \sigma^{2}}} \nonumber\]

This formula has a lot of parts, but once we break down the parts, we’ll see that there are just two things to know. First, let’s identify the parts of the equation:

\(Y_{i}\) is the height of the curve (normal density)
\(\pi\) (pi) is a constant = 3.14159… (R, use pi)
\(\mu\) is the population mean
\(\sigma^{2}\) is the population variance
\(\sigma\) is the square-root of the variance or the population standard deviation
\(e\) is the natural logarithm (R, use exp())
\(X_{i}\) is the individual’s value

Why the Normal distribution is so important in classical statistics

With these distinctions out of the way, the first important message about the normal curve is that it permits us to say how likely (i.e., how probable) a particular value is if the observation comes from a population with mean \(\mu\) and standard deviation \(\sigma\), and the population from which the sample was drawn came from a normal distribution.

The second message: all we need to know to recreate the normal distribution for a set of data is the mean and the variance (or the standard deviation) for the population!! With just these two parameters, we can then determine the expected proportion of observations expected for each value of \(X\). Note — we generally do not know these two because they are population parameters: we must estimate them from samples, using our sample statistics, and that’s where the first big assumption in conducting statistical analyses comes into play!!

Here is an example for calculating the normal distribution when knowing the mean and variance: \(\mu = 5\), \(\sigma^{2} = 10\); thus, the standard deviation is \(\sigma = 3.16\).

The formula becomes \[Y_{i} = \frac{0.398947}{3.16} \cdot e^{\frac{-\left(X_{i} - 5\right)^{2}}{2 \cdot 10}} \nonumber\]

Now, plug in different values of \(X\) (for example, what’s the probability that a value of \(X\) could be 0, 1, 2, …, 10 if we really do have a normal curve with mean = 5, and variance = 10?)

The normal equation returns the proportion of observations in a normal population for each \(X\) value:

When \(i = 5\), \(Y_{5} = 0.12616\). This is the proportion of all data points that have an \(X = 5\) value. When \(i = 1\), \(Y_{1} = 0.019995\). This is the proportion of all data points that have an \(X = 1\) value.

We can keep going, getting the proportion expected for each value of \(X\), then make the plot.

Figure \(\PageIndex{6}\): Frequency expected for a few points \((X=0\) through \(X = 10)\) drawn from a normal distribution, calculated using the formula and example values.

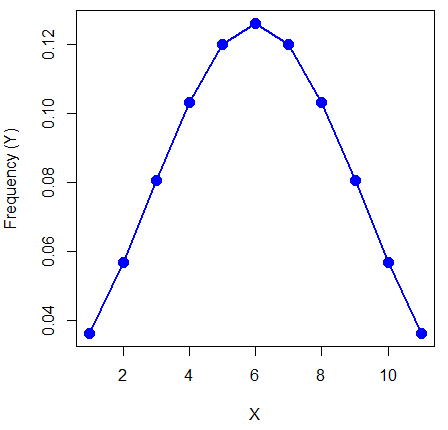
Here’s the R code for the plot

X = seq(0,10, by=1)
Y = (0.398947/3.16)*exp((-1*(X-5)^2)/20)
plot(Y~X, ylab="Frequency (Y)", cex=1.5, pch=19,col="blue")
lines(X,Y, col="blue", lwd=2)

Next up is more about the normal distribution, Chapter 6.7.

---

Questions

1. For a mean of 0 and standard deviation of 1, apply the equation for the normal curve for X = (-4, -3.5, -3, -2.5, -2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4). Plot your results.
2. Sample from a normal distribution with different sample size, means, and standard deviations. Each time, make a histogram and compare the shape of the histograms.