15.9: Model Checking
- Page ID
- 8290
The main focus of this section is regression diagnostics, a term that refers to the art of checking that the assumptions of your regression model have been met, figuring out how to fix the model if the assumptions are violated, and generally to check that nothing “funny” is going on. I refer to this as the “art” of model checking with good reason: it’s not easy, and while there are a lot of fairly standardised tools that you can use to diagnose and maybe even cure the problems that ail your model (if there are any, that is!), you really do need to exercise a certain amount of judgment when doing this. It’s easy to get lost in all the details of checking this thing or that thing, and it’s quite exhausting to try to remember what all the different things are. This has the very nasty side effect that a lot of people get frustrated when trying to learn all the tools, so instead they decide not to do any model checking. This is a bit of a worry!
In this section, I describe several different things you can do to check that your regression model is doing what it’s supposed to. It doesn’t cover the full space of things you could do, but it’s still much more detailed than what I see a lot of people doing in practice; and I don’t usually cover all of this in my intro stats class myself. However, I do think it’s important that you get a sense of what tools are at your disposal, so I’ll try to introduce a bunch of them here. Finally, I should note that this section draws quite heavily from the Fox and Weisberg (2011) text, the book associated with the car package. The car package is notable for providing some excellent tools for regression diagnostics, and the book itself talks about them in an admirably clear fashion. I don’t want to sound too gushy about it, but I do think that Fox and Weisberg (2011) is well worth reading.
Three kinds of residuals
The majority of regression diagnostics revolve around looking at the residuals, and by now you’ve probably formed a sufficiently pessimistic theory of statistics to be able to guess that – precisely because of the fact that we care a lot about the residuals – there are several different kinds of residual that we might consider. In particular, the following three kinds of residual are referred to in this section: “ordinary residuals”, “standardised residuals”, and “Studentised residuals”. There is a fourth kind that you’ll see referred to in some of the Figures, and that’s the “Pearson residual”: however, for the models that we’re talking about in this chapter, the Pearson residual is identical to the ordinary residual.
The first and simplest kind of residuals that we care about are ordinary residuals. These are the actual, raw residuals that I’ve been talking about throughout this chapter. The ordinary residual is just the difference between the fitted value \(\ \hat{Y_i}\) and the observed value Yi. I’ve been using the notation ϵi to refer to the i-th ordinary residual, and by gum I’m going to stick to it. With this in mind, we have the very simple equation
\(\ \epsilon_i = Y_i - \hat{Y_i}\)
This is of course what we saw earlier, and unless I specifically refer to some other kind of residual, this is the one I’m talking about. So there’s nothing new here: I just wanted to repeat myself. In any case, you can get R to output a vector of ordinary residuals, you can use a command like this:
residuals( object = regression.2 )## 1 2 3 4 5 6
## -2.1403095 4.7081942 1.9553640 -2.0602806 0.7194888 -0.4066133
## 7 8 9 10 11 12
## 0.2269987 -1.7003077 0.2025039 3.8524589 3.9986291 -4.9120150
## 13 14 15 16 17 18
## 1.2060134 0.4946578 -2.6579276 -0.3966805 3.3538613 1.7261225
## 19 20 21 22 23 24
## -0.4922551 -5.6405941 -0.4660764 2.7238389 9.3653697 0.2841513
## 25 26 27 28 29 30
## -0.5037668 -1.4941146 8.1328623 1.9787316 -1.5126726 3.5171148
## 31 32 33 34 35 36
## -8.9256951 -2.8282946 6.1030349 -7.5460717 4.5572128 -10.6510836
## 37 38 39 40 41 42
## -5.6931846 6.3096506 -2.1082466 -0.5044253 0.1875576 4.8094841
## 43 44 45 46 47 48
## -5.4135163 -6.2292842 -4.5725232 -5.3354601 3.9950111 2.1718745
## 49 50 51 52 53 54
## -3.4766440 0.4834367 6.2839790 2.0109396 -1.5846631 -2.2166613
## 55 56 57 58 59 60
## 2.2033140 1.9328736 -1.8301204 -1.5401430 2.5298509 -3.3705782
## 61 62 63 64 65 66
## -2.9380806 0.6590736 -0.5917559 -8.6131971 5.9781035 5.9332979
## 67 68 69 70 71 72
## -1.2341956 3.0047669 -1.0802468 6.5174672 -3.0155469 2.1176720
## 73 74 75 76 77 78
## 0.6058757 -2.7237421 -2.2291472 -1.4053822 4.7461491 11.7495569
## 79 80 81 82 83 84
## 4.7634141 2.6620908 -11.0345292 -0.7588667 1.4558227 -0.4745727
## 85 86 87 88 89 90
## 8.9091201 -1.1409777 0.7555223 -0.4107130 0.8797237 -1.4095586
## 91 92 93 94 95 96
## 3.1571385 -3.4205757 -5.7228699 -2.2033958 -3.8647891 0.4982711
## 97 98 99 100
## -5.5249495 4.1134221 -8.2038533 5.6800859One drawback to using ordinary residuals is that they’re always on a different scale, depending on what the outcome variable is and how good the regression model is. That is, Unless you’ve decided to run a regression model without an intercept term, the ordinary residuals will have mean 0; but the variance is different for every regression. In a lot of contexts, especially where you’re only interested in the pattern of the residuals and not their actual values, it’s convenient to estimate the standardised residuals, which are normalised in such a way as to have standard deviation 1. The way we calculate these is to divide the ordinary residual by an estimate of the (population) standard deviation of these residuals. For technical reasons, mumble mumble, the formula for this is:
\(\epsilon_{i}^{\prime}=\dfrac{\epsilon_{i}}{\hat{\sigma} \sqrt{1-h_{i}}}\)
where \(\ \hat{\sigma}\) in this context is the estimated population standard deviation of the ordinary residuals, and hi is the “hat value” of the ith observation. I haven’t explained hat values to you yet (but have no fear,220 it’s coming shortly), so this won’t make a lot of sense. For now, it’s enough to interpret the standardised residuals as if we’d converted the ordinary residuals to z-scores. In fact, that is more or less the truth, it’s just that we’re being a bit fancier. To get the standardised residuals, the command you want is this:
rstandard( model = regression.2 )## 1 2 3 4 5 6
## -0.49675845 1.10430571 0.46361264 -0.47725357 0.16756281 -0.09488969
## 7 8 9 10 11 12
## 0.05286626 -0.39260381 0.04739691 0.89033990 0.95851248 -1.13898701
## 13 14 15 16 17 18
## 0.28047841 0.11519184 -0.61657092 -0.09191865 0.77692937 0.40403495
## 19 20 21 22 23 24
## -0.11552373 -1.31540412 -0.10819238 0.62951824 2.17129803 0.06586227
## 25 26 27 28 29 30
## -0.11980449 -0.34704024 1.91121833 0.45686516 -0.34986350 0.81233165
## 31 32 33 34 35 36
## -2.08659993 -0.66317843 1.42930082 -1.77763064 1.07452436 -2.47385780
## 37 38 39 40 41 42
## -1.32715114 1.49419658 -0.49115639 -0.11674947 0.04401233 1.11881912
## 43 44 45 46 47 48
## -1.27081641 -1.46422595 -1.06943700 -1.24659673 0.94152881 0.51069809
## 49 50 51 52 53 54
## -0.81373349 0.11412178 1.47938594 0.46437962 -0.37157009 -0.51609949
## 55 56 57 58 59 60
## 0.51800753 0.44813204 -0.42662358 -0.35575611 0.58403297 -0.78022677
## 61 62 63 64 65 66
## -0.67833325 0.15484699 -0.13760574 -2.05662232 1.40238029 1.37505125
## 67 68 69 70 71 72
## -0.28964989 0.69497632 -0.24945316 1.50709623 -0.69864682 0.49071427
## 73 74 75 76 77 78
## 0.14267297 -0.63246560 -0.51972828 -0.32509811 1.10842574 2.72171671
## 79 80 81 82 83 84
## 1.09975101 0.62057080 -2.55172097 -0.17584803 0.34340064 -0.11158952
## 85 86 87 88 89 90
## 2.10863391 -0.26386516 0.17624445 -0.09504416 0.20450884 -0.32730740
## 91 92 93 94 95 96
## 0.73475640 -0.79400855 -1.32768248 -0.51940736 -0.91512580 0.11661226
## 97 98 99 100
## -1.28069115 0.96332849 -1.90290258 1.31368144Note that this function uses a different name for the input argument, but it’s still just a linear regression object that the function wants to take as its input here.
The third kind of residuals are Studentised residuals (also called “jackknifed residuals”) and they’re even fancier than standardised residuals. Again, the idea is to take the ordinary residual and divide it by some quantity in order to estimate some standardised notion of the residual, but the formula for doing the calculations this time is subtly different:
\(\epsilon_{i}^{*}=\dfrac{\epsilon_{i}}{\hat{\sigma}_{(-i)} \sqrt{1-h_{i}}}\)
Notice that our estimate of the standard deviation here is written \(\ \hat{\sigma_{-i}}\). What this corresponds to is the estimate of the residual standard deviation that you would have obtained, if you just deleted the ith observation from the data set. This sounds like the sort of thing that would be a nightmare to calculate, since it seems to be saying that you have to run N new regression models (even a modern computer might grumble a bit at that, especially if you’ve got a large data set). Fortunately, some terribly clever person has shown that this standard deviation estimate is actually given by the following equation:
\(\hat{\sigma}_{(-i)}=\hat{\sigma} \sqrt{\dfrac{N-K-1-\epsilon_{i}^{\prime 2}}{N-K-2}}\)
Isn’t that a pip? Anyway, the command that you would use if you wanted to pull out the Studentised residuals for our regression model is
rstudent( model = regression.2 )## 1 2 3 4 5 6
## -0.49482102 1.10557030 0.46172854 -0.47534555 0.16672097 -0.09440368
## 7 8 9 10 11 12
## 0.05259381 -0.39088553 0.04715251 0.88938019 0.95810710 -1.14075472
## 13 14 15 16 17 18
## 0.27914212 0.11460437 -0.61459001 -0.09144760 0.77533036 0.40228555
## 19 20 21 22 23 24
## -0.11493461 -1.32043609 -0.10763974 0.62754813 2.21456485 0.06552336
## 25 26 27 28 29 30
## -0.11919416 -0.34546127 1.93818473 0.45499388 -0.34827522 0.81089646
## 31 32 33 34 35 36
## -2.12403286 -0.66125192 1.43712830 -1.79797263 1.07539064 -2.54258876
## 37 38 39 40 41 42
## -1.33244515 1.50388257 -0.48922682 -0.11615428 0.04378531 1.12028904
## 43 44 45 46 47 48
## -1.27490649 -1.47302872 -1.07023828 -1.25020935 0.94097261 0.50874322
## 49 50 51 52 53 54
## -0.81230544 0.11353962 1.48863006 0.46249410 -0.36991317 -0.51413868
## 55 56 57 58 59 60
## 0.51604474 0.44627831 -0.42481754 -0.35414868 0.58203894 -0.77864171
## 61 62 63 64 65 66
## -0.67643392 0.15406579 -0.13690795 -2.09211556 1.40949469 1.38147541
## 67 68 69 70 71 72
## -0.28827768 0.69311245 -0.24824363 1.51717578 -0.69679156 0.48878534
## 73 74 75 76 77 78
## 0.14195054 -0.63049841 -0.51776374 -0.32359434 1.10974786 2.81736616
## 79 80 81 82 83 84
## 1.10095270 0.61859288 -2.62827967 -0.17496714 0.34183379 -0.11101996
## 85 86 87 88 89 90
## 2.14753375 -0.26259576 0.17536170 -0.09455738 0.20349582 -0.32579584
## 91 92 93 94 95 96
## 0.73300184 -0.79248469 -1.33298848 -0.51744314 -0.91435205 0.11601774
## 97 98 99 100
## -1.28498273 0.96296745 -1.92942389 1.31867548Before moving on, I should point out that you don’t often need to manually extract these residuals yourself, even though they are at the heart of almost all regression diagnostics. That is, the residuals(), rstandard() and rstudent() functions are all useful to know about, but most of the time the various functions that run the diagnostics will take care of these calculations for you. Even so, it’s always nice to know how to actually get hold of these things yourself in case you ever need to do something non-standard.
Three kinds of anomalous data
One danger that you can run into with linear regression models is that your analysis might be disproportionately sensitive to a smallish number of “unusual” or “anomalous” observations. I discussed this idea previously in Section 6.5.2 in the context of discussing the outliers that get automatically identified by the boxplot() function, but this time we need to be much more precise. In the context of linear regression, there are three conceptually distinct ways in which an observation might be called “anomalous”. All three are interesting, but they have rather different implications for your analysis.
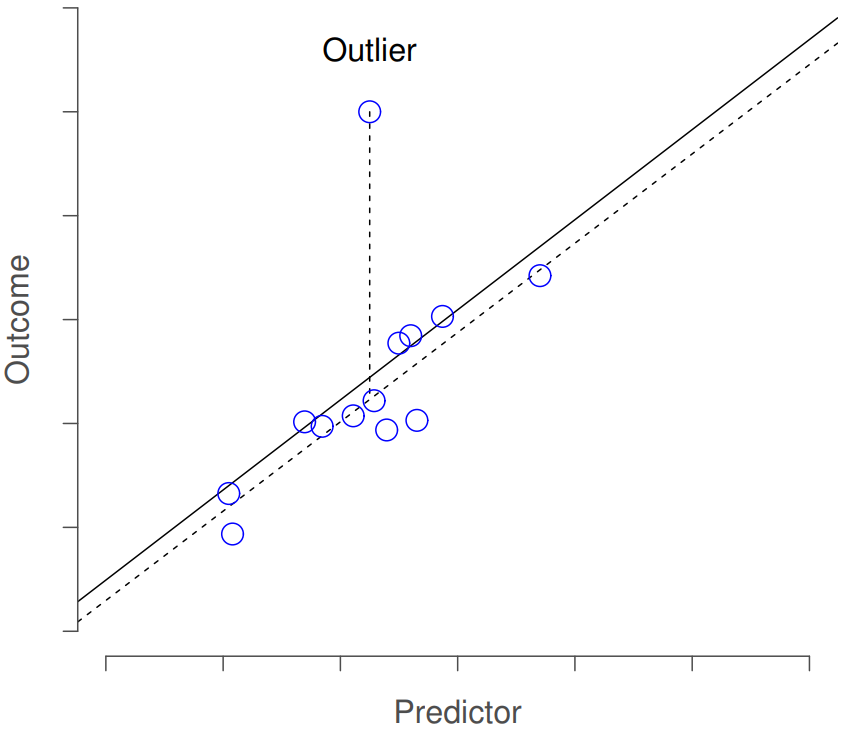
The first kind of unusual observation is an outlier. The definition of an outlier (in this context) is an observation that is very different from what the regression model predicts. An example is shown in Figure 15.7. In practice, we operationalise this concept by saying that an outlier is an observation that has a very large Studentised residual, \(\ {\epsilon_i}^*\). Outliers are interesting: a big outlier might correspond to junk data – e.g., the variables might have been entered incorrectly, or some other defect may be detectable. Note that you shouldn’t throw an observation away just because it’s an outlier. But the fact that it’s an outlier is often a cue to look more closely at that case, and try to find out why it’s so different.
The second way in which an observation can be unusual is if it has high leverage: this happens when the observation is very different from all the other observations. This doesn’t necessarily have to correspond to a large residual: if the observation happens to be unusual on all variables in precisely the same way, it can actually lie very close to the regression line. An example of this is shown in Figure 15.8. The leverage of an observation is operationalised in terms of its hat value, usually written hi. The formula for the hat value is rather complicated221 but its interpretation is not: hi is a measure of the extent to which the i-th observation is “in control” of where the regression line ends up going. You can extract the hat values using the following command:
hatvalues( model = regression.2 )## 1 2 3 4 5 6
## 0.02067452 0.04105320 0.06155445 0.01685226 0.02734865 0.03129943
## 7 8 9 10 11 12
## 0.02735579 0.01051224 0.03698976 0.01229155 0.08189763 0.01882551
## 13 14 15 16 17 18
## 0.02462902 0.02718388 0.01964210 0.01748592 0.01691392 0.03712530
## 19 20 21 22 23 24
## 0.04213891 0.02994643 0.02099435 0.01233280 0.01853370 0.01804801
## 25 26 27 28 29 30
## 0.06722392 0.02214927 0.04472007 0.01039447 0.01381812 0.01105817
## 31 32 33 34 35 36
## 0.03468260 0.04048248 0.03814670 0.04934440 0.05107803 0.02208177
## 37 38 39 40 41 42
## 0.02919013 0.05928178 0.02799695 0.01519967 0.04195751 0.02514137
## 43 44 45 46 47 48
## 0.04267879 0.04517340 0.03558080 0.03360160 0.05019778 0.04587468
## 49 50 51 52 53 54
## 0.03701290 0.05331282 0.04814477 0.01072699 0.04047386 0.02681315
## 55 56 57 58 59 60
## 0.04556787 0.01856997 0.02919045 0.01126069 0.01012683 0.01546412
## 61 62 63 64 65 66
## 0.01029534 0.04428870 0.02438944 0.07469673 0.04135090 0.01775697
## 67 68 69 70 71 72
## 0.04217616 0.01384321 0.01069005 0.01340216 0.01716361 0.01751844
## 73 74 75 76 77 78
## 0.04863314 0.02158623 0.02951418 0.01411915 0.03276064 0.01684599
## 79 80 81 82 83 84
## 0.01028001 0.02920514 0.01348051 0.01752758 0.05184527 0.04583604
## 85 86 87 88 89 90
## 0.05825858 0.01359644 0.03054414 0.01487724 0.02381348 0.02159418
## 91 92 93 94 95 96
## 0.02598661 0.02093288 0.01982480 0.05063492 0.05907629 0.03682026
## 97 98 99 100
## 0.01817919 0.03811718 0.01945603 0.01373394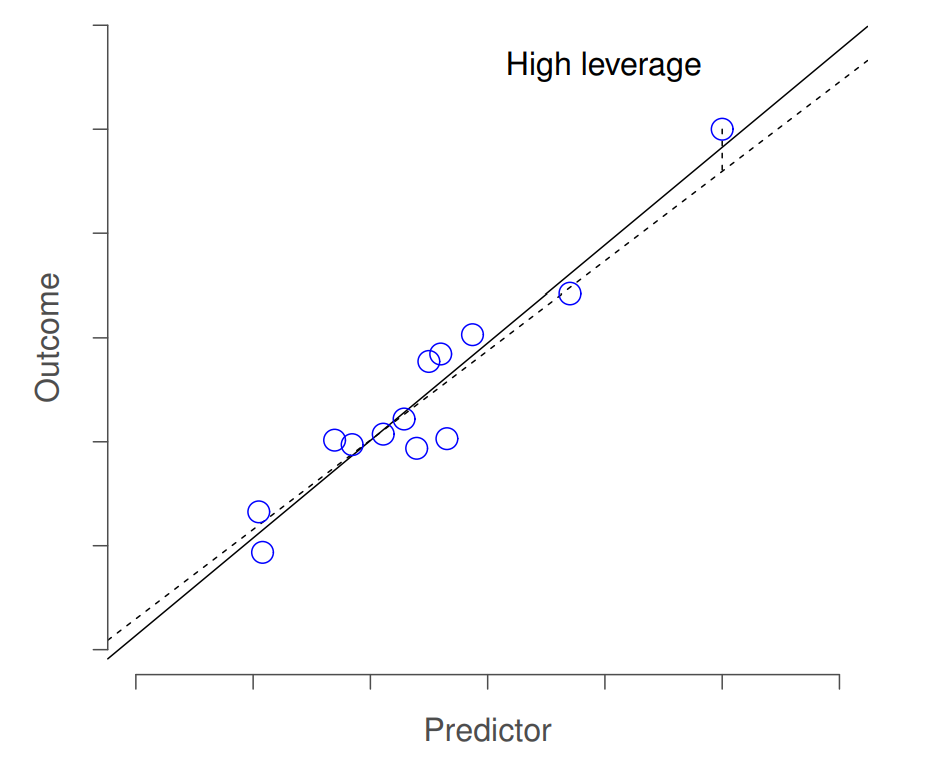
In general, if an observation lies far away from the other ones in terms of the predictor variables, it will have a large hat value (as a rough guide, high leverage is when the hat value is more than 2-3 times the average; and note that the sum of the hat values is constrained to be equal to K+1). High leverage points are also worth looking at in more detail, but they’re much less likely to be a cause for concern unless they are also outliers. % guide from Venables and Ripley.
This brings us to our third measure of unusualness, the influence of an observation. A high influence observation is an outlier that has high leverage. That is, it is an observation that is very different to all the other ones in some respect, and also lies a long way from the regression line. This is illustrated in Figure 15.9. Notice the contrast to the previous two figures: outliers don’t move the regression line much, and neither do high leverage points. But something that is an outlier and has high leverage… that has a big effect on the regression line.
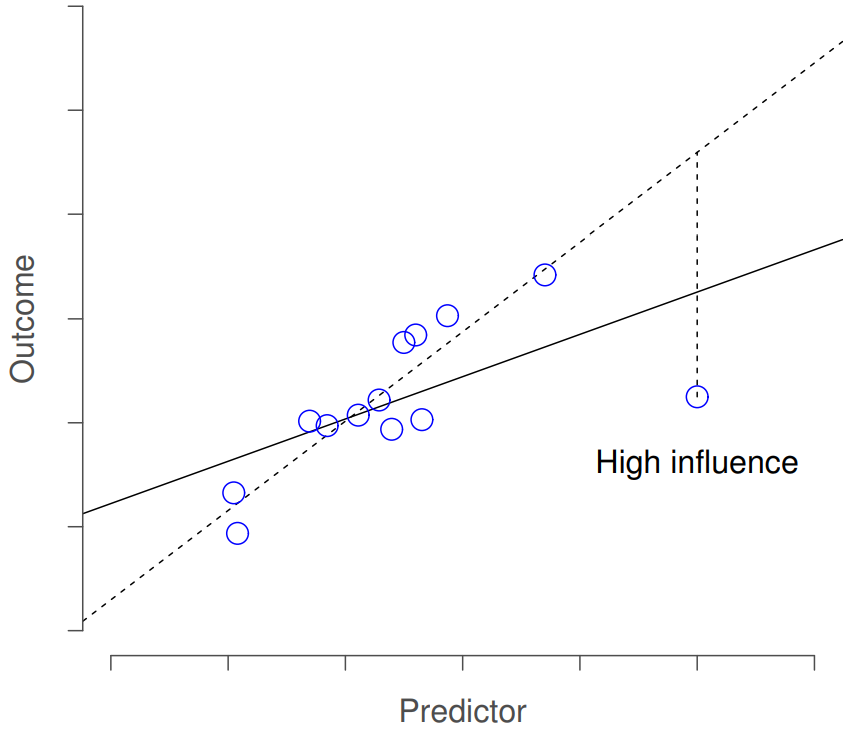
That’s why we call these points high influence; and it’s why they’re the biggest worry. We operationalise influence in terms of a measure known as Cook’s distance,
\(D_{i}=\dfrac{\epsilon_{i}^{* 2}}{K+1} \times \dfrac{h_{i}}{1-h_{i}}\)
Notice that this is a multiplication of something that measures the outlier-ness of the observation (the bit on the left), and something that measures the leverage of the observation (the bit on the right). In other words, in order to have a large Cook’s distance, an observation must be a fairly substantial outlier and have high leverage. In a stunning turn of events, you can obtain these values using the following command:
cooks.distance( model = regression.2 )## 1 2 3 4 5
## 1.736512e-03 1.740243e-02 4.699370e-03 1.301417e-03 2.631557e-04
## 6 7 8 9 10
## 9.697585e-05 2.620181e-05 5.458491e-04 2.876269e-05 3.288277e-03
## 11 12 13 14 15
## 2.731835e-02 8.296919e-03 6.621479e-04 1.235956e-04 2.538915e-03
## 16 17 18 19 20
## 5.012283e-05 3.461742e-03 2.098055e-03 1.957050e-04 1.780519e-02
## 21 22 23 24 25
## 8.367377e-05 1.649478e-03 2.967594e-02 2.657610e-05 3.448032e-04
## 26 27 28 29 30
## 9.093379e-04 5.699951e-02 7.307943e-04 5.716998e-04 2.459564e-03
## 31 32 33 34 35
## 5.214331e-02 6.185200e-03 2.700686e-02 5.467345e-02 2.071643e-02
## 36 37 38 39 40
## 4.606378e-02 1.765312e-02 4.689817e-02 2.316122e-03 7.012530e-05
## 41 42 43 44 45
## 2.827824e-05 1.076083e-02 2.399931e-02 3.381062e-02 1.406498e-02
## 46 47 48 49 50
## 1.801086e-02 1.561699e-02 4.179986e-03 8.483514e-03 2.444787e-04
## 51 52 53 54 55
## 3.689946e-02 7.794472e-04 1.941235e-03 2.446230e-03 4.270361e-03
## 56 57 58 59 60
## 1.266609e-03 1.824212e-03 4.804705e-04 1.163181e-03 3.187235e-03
## 61 62 63 64 65
## 1.595512e-03 3.703826e-04 1.577892e-04 1.138165e-01 2.827715e-02
## 66 67 68 69 70
## 1.139374e-02 1.231422e-03 2.260006e-03 2.241322e-04 1.028479e-02
## 71 72 73 74 75
## 2.841329e-03 1.431223e-03 3.468538e-04 2.941757e-03 2.738249e-03
## 76 77 78 79 80
## 5.045357e-04 1.387108e-02 4.230966e-02 4.187440e-03 3.861831e-03
## 81 82 83 84 85
## 2.965826e-02 1.838888e-04 2.149369e-03 1.993929e-04 9.168733e-02
## 86 87 88 89 90
## 3.198994e-04 3.262192e-04 4.547383e-05 3.400893e-04 7.881487e-04
## 91 92 93 94 95
## 4.801204e-03 4.493095e-03 1.188427e-02 4.796360e-03 1.752666e-02
## 96 97 98 99 100
## 1.732793e-04 1.012302e-02 1.225818e-02 2.394964e-02 8.010508e-03As a rough guide, Cook’s distance greater than 1 is often considered large (that’s what I typically use as a quick and dirty rule), though a quick scan of the internet and a few papers suggests that 4/N has also been suggested as a possible rule of thumb.
As hinted above, you don’t usually need to make use of these functions, since you can have R automatically draw the critical plots.222 For the regression.2 model, these are the plots showing Cook’s distance (Figure 15.10) and the more detailed breakdown showing the scatter plot of the Studentised residual against leverage (Figure 15.11). To draw these, we can use the plot() function. When the main argument x to this function is a linear model object, it will draw one of six different plots, each of which is quite useful for doing regression diagnostics. You specify which one you want using the which argument (a number between 1 and 6). If you don’t do this then R will draw all six. The two plots of interest to us in this context are generated using the following commands:
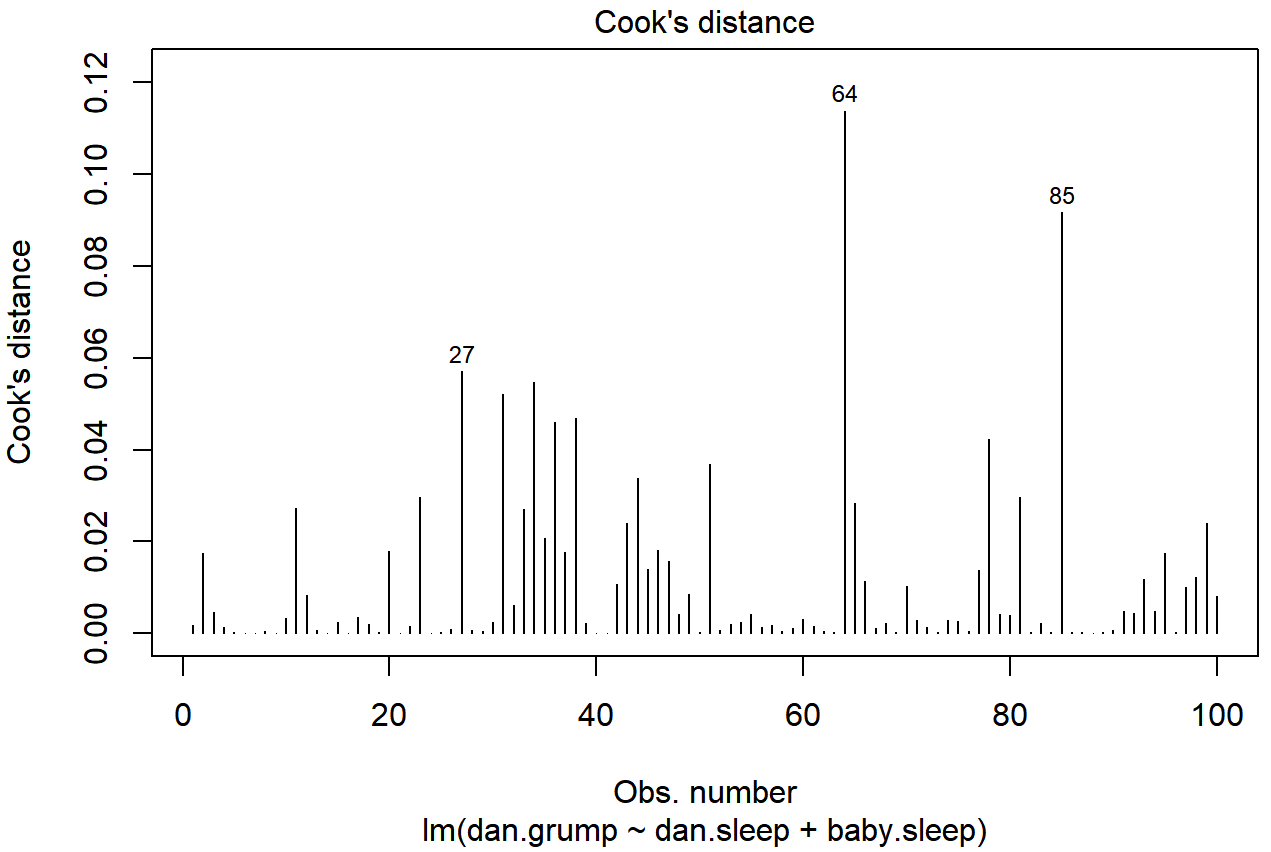
plot() function when the input is a linear regression object. It is obtained by setting which=4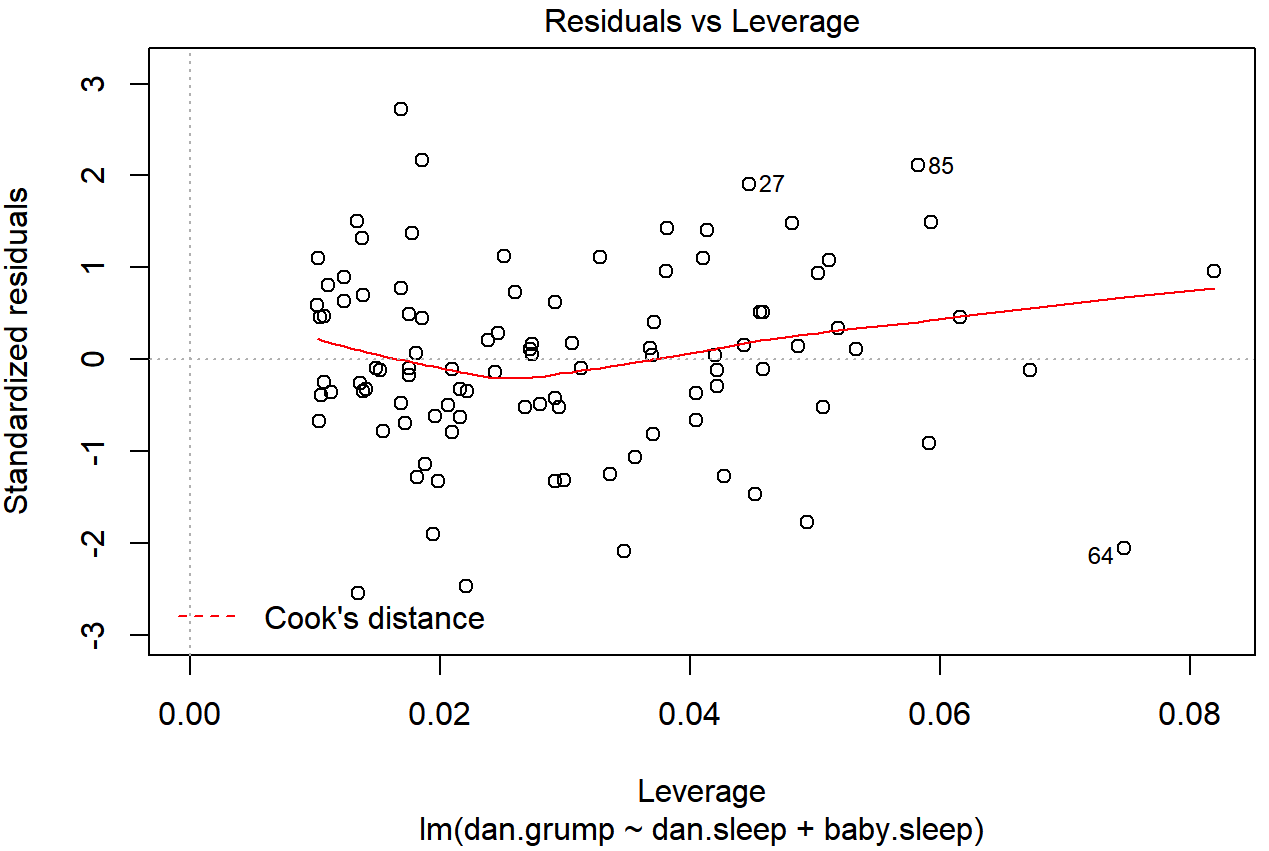
plot() function when the input is a linear regression object. It is obtained by setting which=5.An obvious question to ask next is, if you do have large values of Cook’s distance, what should you do? As always, there’s no hard and fast rules. Probably the first thing to do is to try running the regression with that point excluded and see what happens to the model performance and to the regression coefficients. If they really are substantially different, it’s time to start digging into your data set and your notes that you no doubt were scribbling as your ran your study; try to figure out why the point is so different. If you start to become convinced that this one data point is badly distorting your results, you might consider excluding it, but that’s less than ideal unless you have a solid explanation for why this particular case is qualitatively different from the others and therefore deserves to be handled separately.223 To give an example, let’s delete the observation from day 64, the observation with the largest Cook’s distance for the regression.2 model. We can do this using the subset argument:
lm( formula = dan.grump ~ dan.sleep + baby.sleep, # same formula
data = parenthood, # same data frame...
subset = -64 # ...but observation 64 is deleted
)##
## Call:
## lm(formula = dan.grump ~ dan.sleep + baby.sleep, data = parenthood,
## subset = -64)
##
## Coefficients:
## (Intercept) dan.sleep baby.sleep
## 126.3553 -8.8283 -0.1319As you can see, those regression coefficients have barely changed in comparison to the values we got earlier. In other words, we really don’t have any problem as far as anomalous data are concerned.
Checking the normality of the residuals
Like many of the statistical tools we’ve discussed in this book, regression models rely on a normality assumption. In this case, we assume that the residuals are normally distributed. The tools for testing this aren’t fundamentally different to those that we discussed earlier in Section 13.9. Firstly, I firmly believe that it never hurts to draw an old fashioned histogram. The command I use might be something like this:
hist( x = residuals( regression.2 ), # data are the residuals
xlab = "Value of residual", # x-axis label
main = "", # no title
breaks = 20 # lots of breaks
)The resulting plot is shown in Figure 15.12, and as you can see the plot looks pretty damn close to normal, almost unnaturally so.
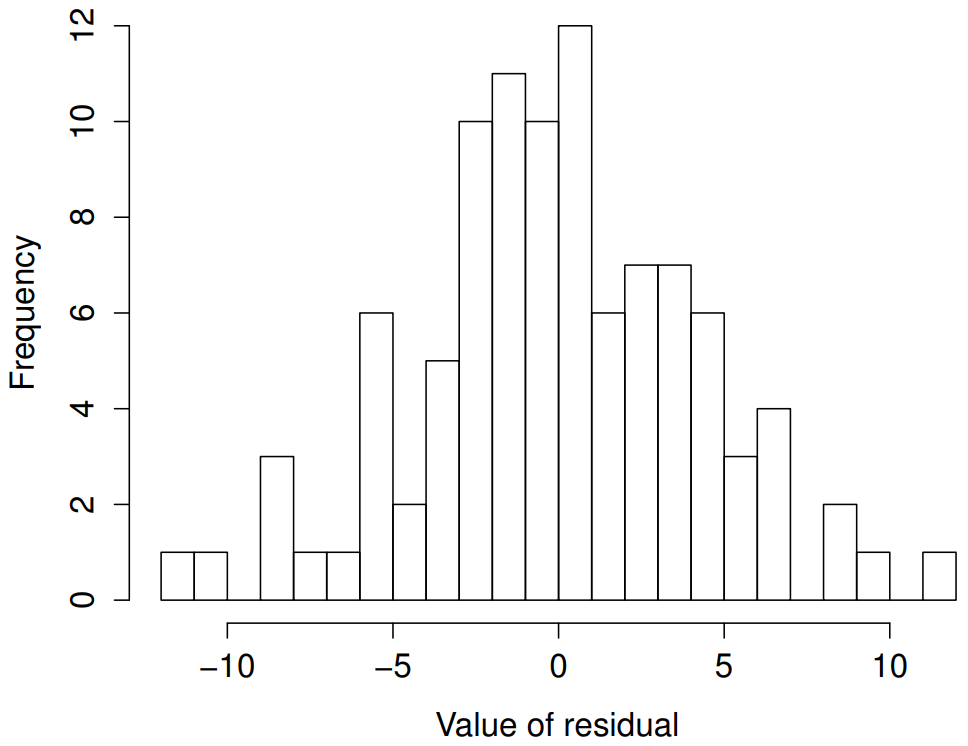
regression.2 model. These residuals look very close to being normally distributed, much moreso than is typically seen with real data. This shouldn’t surprise you… they aren’t real data, and they aren’t real residuals!I could also run a Shapiro-Wilk test to check, using the shapiro.test() function; the W value of .99, at this sample size, is non-significant (p=.84), again suggesting that the normality assumption isn’t in any danger here. As a third measure, we might also want to draw a QQ-plot using the qqnorm() function. The QQ plot is an excellent one to draw, and so you might not be surprised to discover that it’s one of the regression plots that we can produce using the plot() function:
plot( x = regression.2, which = 2 ) # Figure @ref{fig:regressionplot2}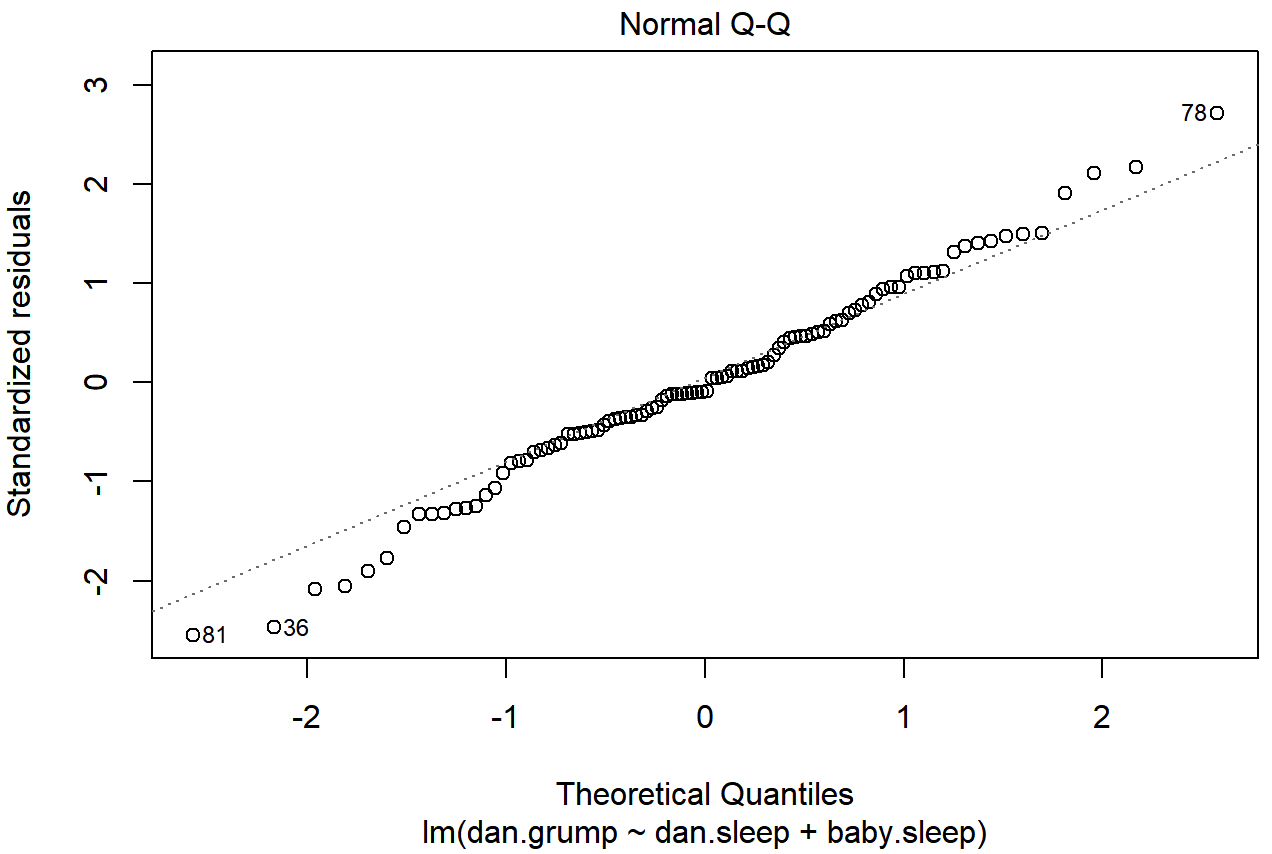
plot() function when the input is a linear regression object. It is obtained by setting which=2.The output is shown in Figure 15.13, showing the standardised residuals plotted as a function of their theoretical quantiles according to the regression model. The fact that the output appends the model specification to the picture is nice.
Checking the linearity of the relationship
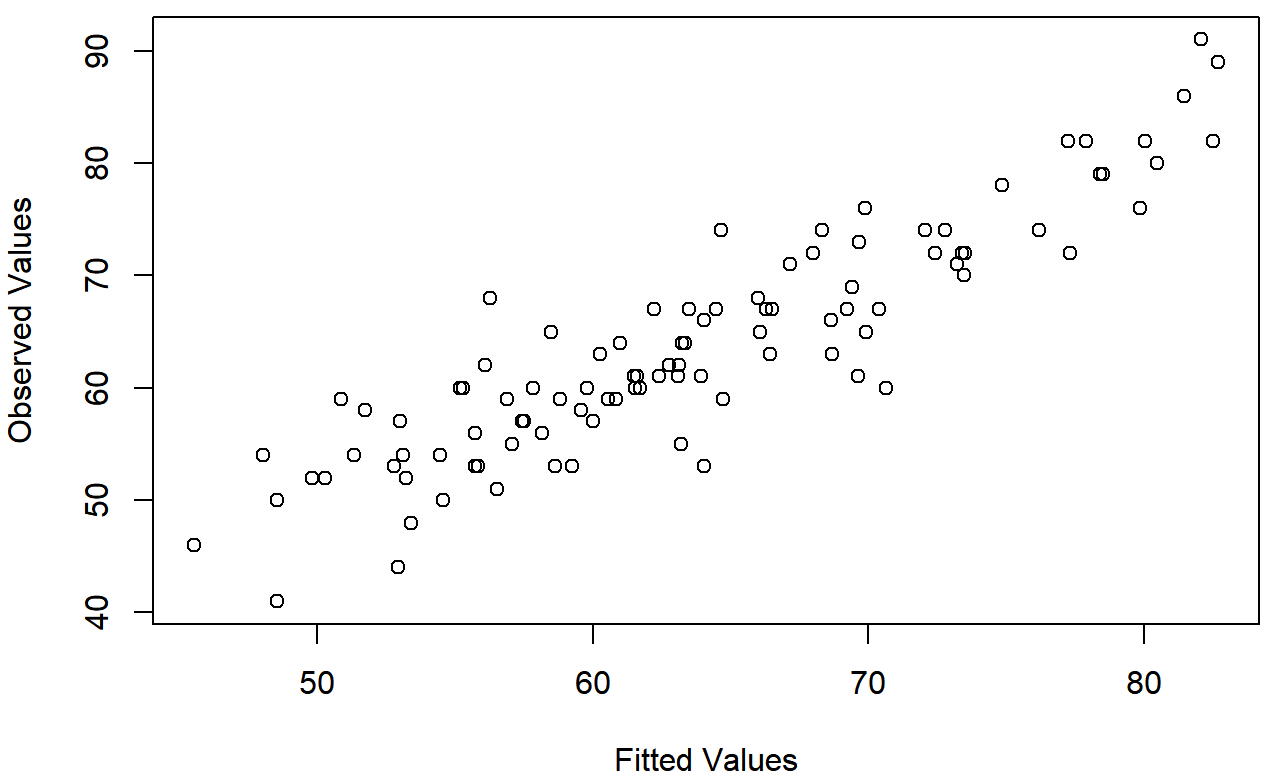
The third thing we might want to test is the linearity of the relationships between the predictors and the outcomes. There’s a few different things that you might want to do in order to check this. Firstly, it never hurts to just plot the relationship between the fitted values \(\ \hat{Y_i}\) and the observed values Yi for the outcome variable, as illustrated in Figure 15.14. To draw this we could use the fitted.values() function to extract the \(\ \hat{Y_i}\) values in much the same way that we used the residuals() function to extract the ϵi values. So the commands to draw this figure might look like this:
yhat.2 <- fitted.values( object = regression.2 )
plot( x = yhat.2,
y = parenthood$dan.grump,
xlab = "Fitted Values",
ylab = "Observed Values"
)One of the reasons I like to draw these plots is that they give you a kind of “big picture view”. If this plot looks approximately linear, then we’re probably not doing too badly (though that’s not to say that there aren’t problems). However, if you can see big departures from linearity here, then it strongly suggests that you need to make some changes.
In any case, in order to get a more detailed picture it’s often more informative to look at the relationship between the fitted values and the residuals themselves. Again, we could draw this plot using low level commands, but there’s an easier way. Just plot() the regression model, and select which = 1:
plot(x = regression.2, which = 1)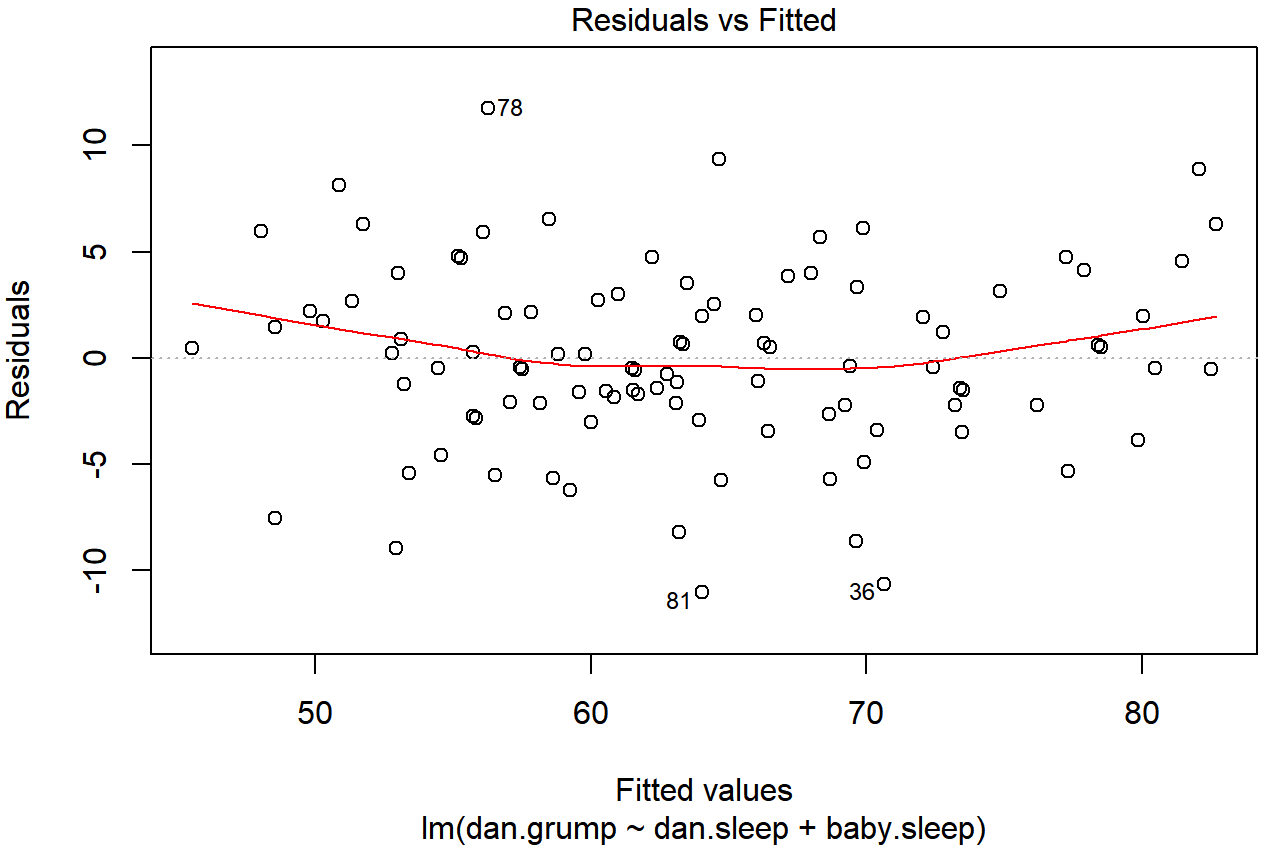
regression.2, with a line showing the relationship between the two. If this is horizontal and straight, then we can feel reasonably confident that the “average residual” for all “fitted values” is more or less the same. This is one of the standard regression plots produced by the plot() function when the input is a linear regression object. It is obtained by setting which=1.The output is shown in Figure 15.15. As you can see, not only does it draw the scatterplot showing the fitted value against the residuals, it also plots a line through the data that shows the relationship between the two. Ideally, this should be a straight, perfectly horizontal line. There’s some hint of curvature here, but it’s not clear whether or not we be concerned.
A somewhat more advanced version of the same plot is produced by the residualPlots() function in the car package. This function not only draws plots comparing the fitted values to the residuals, it does so for each individual predictor. The command is and the resulting plots are shown in Figure 15.16.
residualPlots( model = regression.2 ) ## Loading required package: carData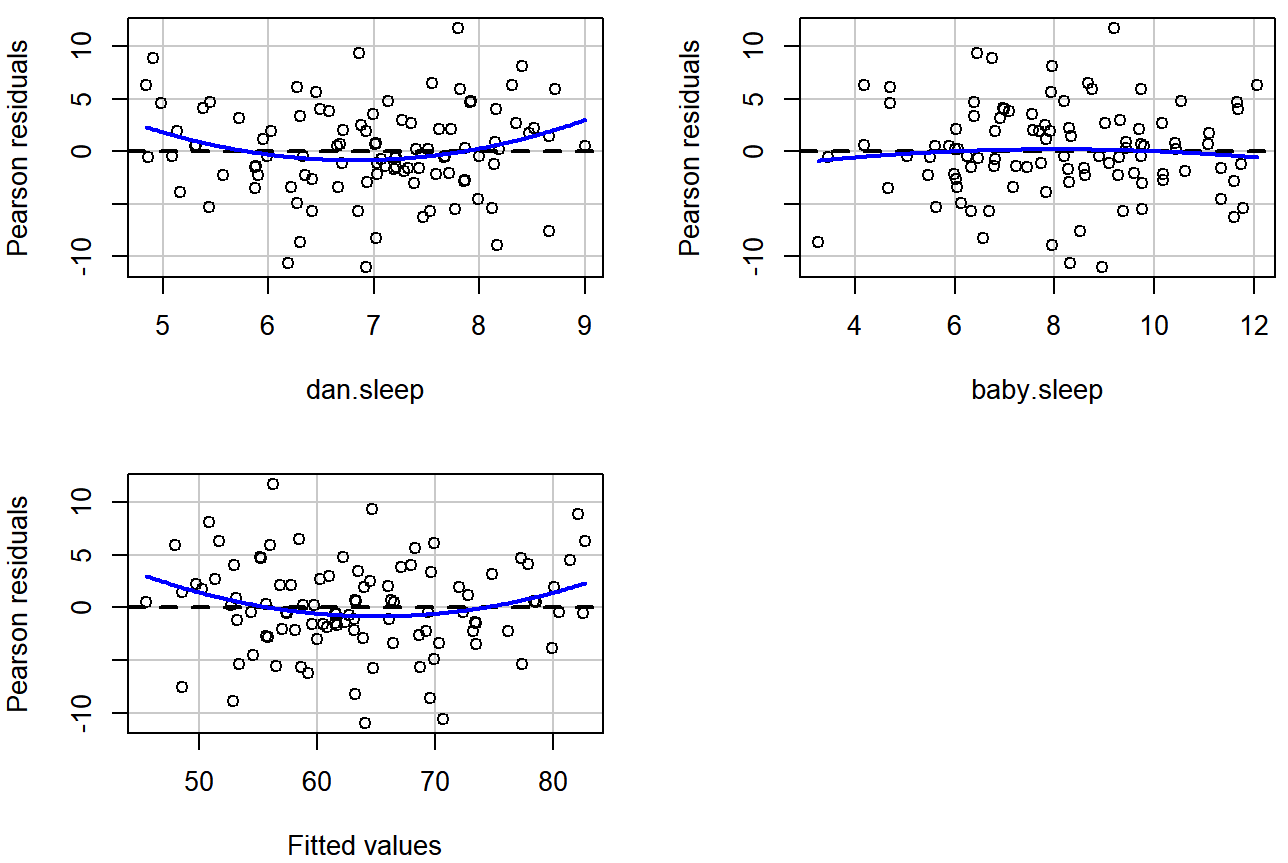
regression.2, along with similar plots for the two predictors individually. This plot is produced by the residualPlots() function in the car package. Note that it refers to the residuals as “Pearson residuals”, but in this context these are the same as ordinary residuals.## Test stat Pr(>|Test stat|)
## dan.sleep 2.1604 0.03323 *
## baby.sleep -0.5445 0.58733
## Tukey test 2.1615 0.03066 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Note that this function also reports the results of a bunch of curvature tests. For a predictor variable X in some regression model, this test is equivalent to adding a new predictor to the model corresponding to X2, and running the t-test on the b coefficient associated with this new predictor. If it comes up significant, it implies that there is some nonlinear relationship between the variable and the residuals.
The third line here is the Tukey test, which is basically the same test, except that instead of squaring one of the predictors and adding it to the model, you square the fitted-value. In any case, the fact that the curvature tests have come up significant is hinting that the curvature that we can see in Figures 15.15 and 15.16 is genuine;224 although it still bears remembering that the pattern in Figure 15.14 is pretty damn straight: in other words the deviations from linearity are pretty small, and probably not worth worrying about.
In a lot of cases, the solution to this problem (and many others) is to transform one or more of the variables. We discussed the basics of variable transformation in Sections 7.2 and (mathfunc), but I do want to make special note of one additional possibility that I didn’t mention earlier: the Box-Cox transform. The Box-Cox function is a fairly simple one, but it’s very widely used
\(f(x, \lambda)=\dfrac{x^{\lambda}-1}{\lambda}\)
for all values of λ except λ=0. When λ=0 we just take the natural logarithm (i.e., ln(x)). You can calculate it using the boxCox() function in the car package. Better yet, if what you’re trying to do is convert a data to normal, or as normal as possible, there’s the powerTransform() function in the car package that can estimate the best value of λ. Variable transformation is another topic that deserves a fairly detailed treatment, but (again) due to deadline constraints, it will have to wait until a future version of this book.
Checking the homogeneity of variance
The regression models that we’ve talked about all make a homogeneity of variance assumption: the variance of the residuals is assumed to be constant. The “default” plot that R provides to help with doing this (which = 3 when using plot()) shows a plot of the square root of the size of the residual \(\ \sqrt{|\epsilon_i|}\), as a function of the fitted value \(\ \hat{Y_i}\). We can produce the plot using the following command,
plot(x = regression.2, which = 3)and the resulting plot is shown in Figure 15.17. Note that this plot actually uses the standardised residuals (i.e., converted to z scores) rather than the raw ones, but it’s immaterial from our point of view. What we’re looking to see here is a straight, horizontal line running through the middle of the plot.
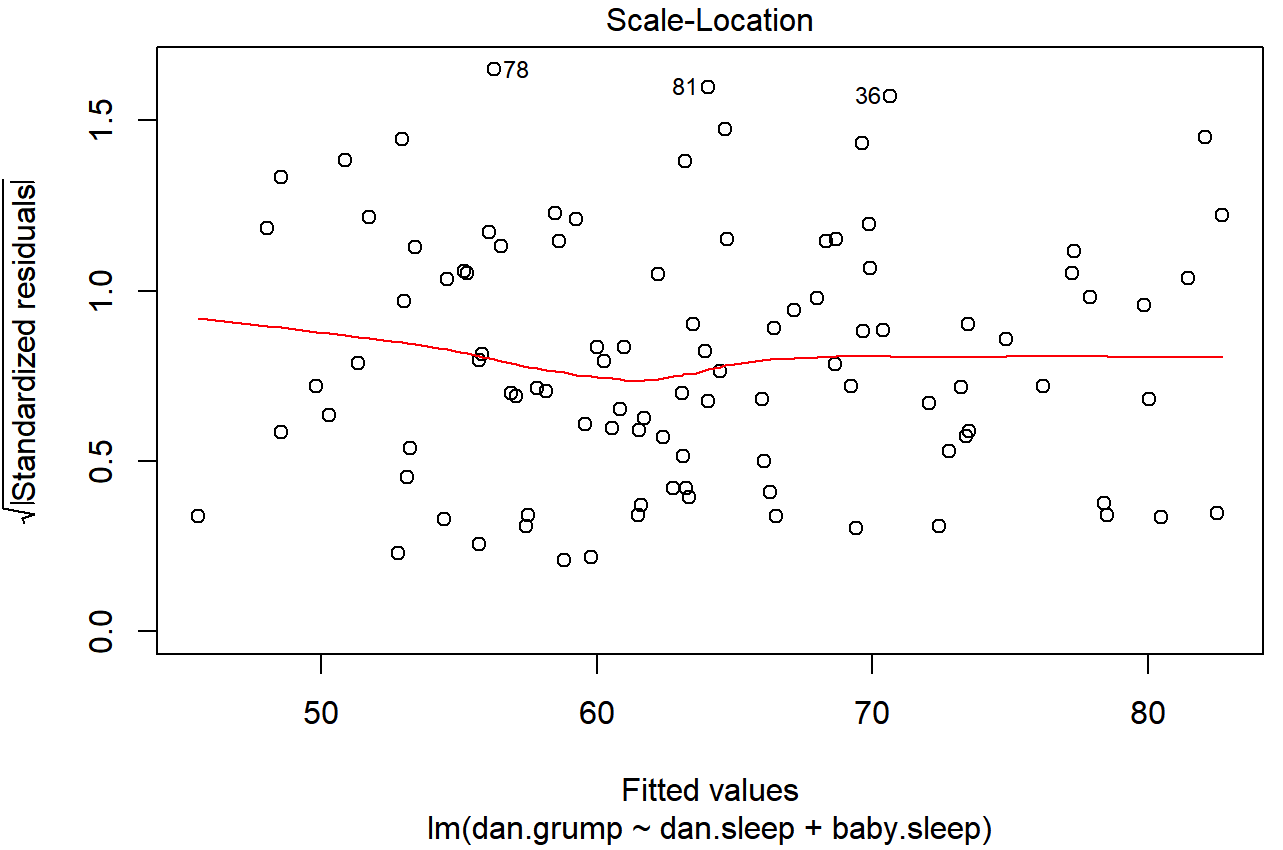
plot() function when the input is a linear regression object. It is obtained by setting which=3.A slightly more formal approach is to run hypothesis tests. The car package provides a function called ncvTest() (non-constant variance test) that can be used for this purpose (Cook and Weisberg 1983). I won’t explain the details of how it works, other than to say that the idea is that what you do is run a regression to see if there is a relationship between the squared residuals ϵi and the fitted values \(\ \hat{Y_i}\), or possibly to run a regression using all of the original predictors instead of just \(\ \hat{Y_i}\).225 Using the default settings, the ncvTest() looks for a relationship between \(\ \hat{Y_i}\) and the variance of the residuals, making it a straightforward analogue of Figure 15.17. So if we run it for our model,
ncvTest( regression.2 )## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 0.09317511, Df = 1, p = 0.76018We see that our original impression was right: there’s no violations of homogeneity of variance in this data.
It’s a bit beyond the scope of this chapter to talk too much about how to deal with violations of homogeneity of variance, but I’ll give you a quick sense of what you need to consider. The main thing to worry about, if homogeneity of variance is violated, is that the standard error estimates associated with the regression coefficients are no longer entirely reliable, and so your t tests for the coefficients aren’t quite right either. A simple fix to the problem is to make use of a “heteroscedasticity corrected covariance matrix” when estimating the standard errors. These are often called sandwich estimators, for reasons that only make sense if you understand the maths at a low level226 have implemented as the default in the hccm() function is a tweak on this, proposed by Long and Ervin (2000). This version uses \(\Sigma=\operatorname{diag}\left(\epsilon_{i}^{2} /\left(1-h_{i}^{2}\right)\right)\), where hi is the ith hat value. Gosh, regression is fun, isn’t it?] You don’t need to understand what this means (not for an introductory class), but it might help to note that there’s a hccm() function in the car() package that does it. Better yet, you don’t even need to use it. You can use the coeftest() function in the lmtest package, but you need the car package loaded:
library(lmtest)
library(car)
coeftest( regression.2, vcov= hccm )##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 125.965566 3.247285 38.7910 <2e-16 ***
## dan.sleep -8.950250 0.615820 -14.5339 <2e-16 ***
## baby.sleep 0.010524 0.291565 0.0361 0.9713
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Not surprisingly, these t tests are pretty much identical to the ones that we saw when we used the summary(regression.2) command earlier; because the homogeneity of variance assumption wasn’t violated. But if it had been, we might have seen some more substantial differences.
Checking for collinearity
The last kind of regression diagnostic that I’m going to discuss in this chapter is the use of variance inflation factors (VIFs), which are useful for determining whether or not the predictors in your regression model are too highly correlated with each other. There is a variance inflation factor associated with each predictor Xk in the model, and the formula for the k-th VIF is:
\(\mathrm{VIF}_{k}=\dfrac{1}{1-R_{(-k)}^{2}}\)
where \(\ {R^2}_{(-k)}\) refers to R-squared value you would get if you ran a regression using Xk as the outcome variable, and all the other X variables as the predictors. The idea here is that \(\ {R^2}_{(-k)}\) is a very good measure of the extent to which Xk is correlated with all the other variables in the model. Better yet, the square root of the VIF is pretty interpretable: it tells you how much wider the confidence interval for the corresponding coefficient bk is, relative to what you would have expected if the predictors are all nice and uncorrelated with one another. If you’ve only got two predictors, the VIF values are always going to be the same, as we can see if we use the vif() function (car package)…
vif( mod = regression.2 )## dan.sleep baby.sleep
## 1.651038 1.651038And since the square root of 1.65 is 1.28, we see that the correlation between our two predictors isn’t causing much of a problem.
To give a sense of how we could end up with a model that has bigger collinearity problems, suppose I were to run a much less interesting regression model, in which I tried to predict the day on which the data were collected, as a function of all the other variables in the data set. To see why this would be a bit of a problem, let’s have a look at the correlation matrix for all four variables:
cor( parenthood )## dan.sleep baby.sleep dan.grump day
## dan.sleep 1.00000000 0.62794934 -0.90338404 -0.09840768
## baby.sleep 0.62794934 1.00000000 -0.56596373 -0.01043394
## dan.grump -0.90338404 -0.56596373 1.00000000 0.07647926
## day -0.09840768 -0.01043394 0.07647926 1.00000000We have some fairly large correlations between some of our predictor variables! When we run the regression model and look at the VIF values, we see that the collinearity is causing a lot of uncertainty about the coefficients. First, run the regression…
regression.3 <- lm( day ~ baby.sleep + dan.sleep + dan.grump, parenthood )and second, look at the VIFs…
vif( regression.3 )## baby.sleep dan.sleep dan.grump
## 1.651064 6.102337 5.437903Yep, that’s some mighty fine collinearity you’ve got there.


