5.1: Important Distributions
- Page ID
- 3140
In this chapter, we describe the discrete probability distributions and the continuous probability densities that occur most often in the analysis of experiments. We will also show how one simulates these distributions and densities on a computer.
Discrete Uniform Distribution
In Chapter 1, we saw that in many cases, we assume that all outcomes of an experiment are equally likely. If \(X\) is a random variable which represents the outcome of an experiment of this type, then we say that \(X\) is uniformly distributed. If the sample space \(S\) is of size \(n\), where \(0 < n < \infty\), then the distribution function \(m(\omega)\) is defined to be \(1/n\) for all \(\omega \in S\). As is the case with all of the discrete probability distributions discussed in this chapter, this experiment can be simulated on a computer using the program GeneralSimulation. However, in this case, a faster algorithm can be used instead. (This algorithm was described in Chapter 1; we repeat the description here for completeness.) The expression \[1 + \lfloor n\,(rnd)\rfloor\] takes on as a value each integer between 1 and \(n\) with probability \(1/n\) (the notation \(\lfloor x \rfloor\) denotes the greatest integer not exceeding \(x\)). Thus, if the possible outcomes of the experiment are labelled \(\omega_1\ \omega_2,\ \ldots,\ \omega_n\), then we use the above expression to represent the subscript of the output of the experiment.
If the sample space is a countably infinite set, such as the set of positive integers, then it is not possible to have an experiment which is uniform on this set (see Exercise 5.1.102). If the sample space is an uncountable set, with positive, finite length, such as the interval \([0, 1]\), then we use continuous density functions (see Section 2).
Binomial Distribution
The binomial distribution with parameters \(n\), \(p\), and \(k\) was defined in Chapter 3. It is the distribution of the random variable which counts the number of heads which occur when a coin is tossed \(n\) times, assuming that on any one toss, the probability that a head occurs is \(p\). The distribution function is given by the formula \[b(n, p, k) = {n \choose k}p^k q^{n-k}\ ,\] where \(q = 1 - p\).
One straightforward way to simulate a binomial random variable \(X\) is to compute the sum of \(n\) independent \(0-1\) random variables, each of which take on the value 1 with probability \(p\).
Geometric Distribution
Consider a Bernoulli trials process continued for an infinite number of trials; for example, a coin tossed an infinite sequence of times. Thus, we can determine the distribution for any random variable \(X\) relating to the experiment provided \(P(X = a)\) can be computed in terms of a finite number of trials. For example, let \(T\) be the number of trials up to and including the first success. Then
\[\begin{aligned} P(T = 1) & = & p\ , \\ P(T = 2) & = & qp\ , \\ P(T = 3) & = & q^2p\ , \\\end{aligned}\]
and in general,
\[P(T = n) = q^{n-1}p\ .\]
To show that this is a distribution, we must show that \[p + qp + q^2p + \cdots = 1\ .\]
The left-hand expression is just a geometric series with first term \(p\) and common ratio \(q\), so its sum is \[{p\over{1-q}}\] which equals 1.
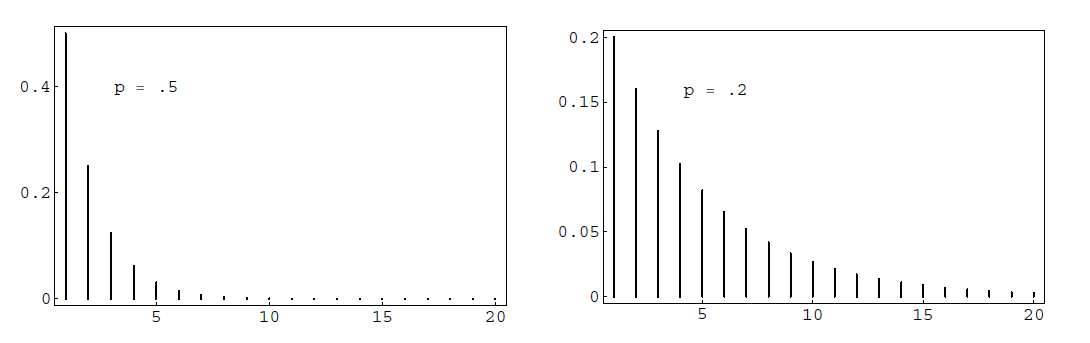
In Figure \(\PageIndex{1}\)we have plotted this distribution using the program GeometricPlot for the cases \(p = .5\) and \(p = .2\). We see that as \(p\) decreases we are more likely to get large values for \(T\), as would be expected. In both cases, the most probable value for \(T\) is 1. This will always be true since \[\frac {P(T = j + 1)}{P(T = j)} = q < 1\ .\]
In general, if \(0 < p < 1\), and \(q = 1 - p\), then we say that the random variable \(T\) has a geometric distribution if \[P(T = j) = q^{j - 1}p\ ,\] for \(j = 1,\ 2,\ 3,\ \ldots\).
To simulate the geometric distribution with parameter \(p\), we can simply compute a sequence of random numbers in \([0, 1)\), stopping when an entry does not exceed \(p\). However, for small values of \(p\), this is time-consuming (taking, on the average, \(1/p\) steps). We now describe a method whose running time does not depend upon the size of \(p\). Define \(Y\) to be the smallest integer satisfying the inequality
\[1 - q^Y \ge rnd\ .\label{eq 5.3}\]
Then we have
\[\begin{aligned} P(Y=j) & =P\left(1-q^j \geq r n d>1-q^{j-1}\right) \\ & =q^{j-1}-q^j \\ & =q^{j-1}(1-q) \\ & =q^{j-1} p .\end{aligned}\]
Thus, \(Y\) is geometrically distributed with parameter \(p\). To generate \(Y\), all we have to do is solve Equation 5.1 for \(Y\). We obtain
\[Y = \Biggl\lceil \frac{\log(1-rnd)}{\log q} \Biggr\rceil\ ,\]
where the notation \(\lceil x \rceil\) means the least integer which is greater than or equal to \(x\). Since \(\log(1-rnd)\) and \(\log(rnd)\) are identically distributed, \(Y\) can also be generated using the equation
\[Y=\left\lceil\frac{\log \; r n d}{\log q}\right\rceil\]
The geometric distribution plays an important role in the theory of queues, or waiting lines. For example, suppose a line of customers waits for service at a counter. It is often assumed that, in each small time unit, either 0 or 1 new customers arrive at the counter. The probability that a customer arrives is \(p\) and that no customer arrives is \(q = 1 - p\). Then the time \(T\) until the next arrival has a geometric distribution. It is natural to ask for the probability that no customer arrives in the next \(k\) time units, that is, for \(P(T > k)\). This is given by
\[\begin{aligned} P(T > k) = \sum_{j = k+1}^\infty q^{j-1}p & = & q^k(p + qp + q^2p + \cdots) \\ & = & q^k\ .\end{aligned}\]
This probability can also be found by noting that we are asking for no successes (i.e., arrivals) in a sequence of \(k\) consecutive time units, where the probability of a success in any one time unit is \(p\). Thus, the probability is just \(q^k\), since arrivals in any two time units are independent events.
It is often assumed that the length of time required to service a customer also has a geometric distribution but with a different value for \(p\). This implies a rather special property of the service time. To see this, let us compute the conditional probability \[P(T > r + s\,|\,T > r) = \frac{P(T > r + s)}{P(T > r)} = \frac {q^{r + s}}{q^r} = q^s\ .\] Thus, the probability that the customer’s service takes \(s\) more time units is independent of the length of time \(r\) that the customer has already been served. Because of this interpretation, this property is called the “memoryless" property, and is also obeyed by the exponential distribution. (Fortunately, not too many service stations have this property.)
Negative Binomial Distribution
Suppose we are given a coin which has probability \(p\) of coming up heads when it is tossed. We fix a positive integer \(k\), and toss the coin until the \(k\)th head appears. We let \(X\) represent the number of tosses. When \(k = 1\), \(X\) is geometrically distributed. For a general \(k\), we say that \(X\) has a negative binomial distribution. We now calculate the probability distribution of \(X\). If \(X = x\), then it must be true that there were exactly \(k-1\) heads thrown in the first \(x-1\) tosses, and a head must have been thrown on the \(x\)th toss. There are
\[\binom{x-1}{k-1}\]
sequences of length \(x\) with these properties, and each of them is assigned the same probability, namely \[p^{k-1}q^{x-k}\ .\] Therefore, if we define \[u(x, k, p) = P(X = x)\ ,\] then
\[u(x, k, p) = \binom{x-1}{k-1}p^kq^{x-k}\ .\]
One can simulate this on a computer by simulating the tossing of a coin. The following algorithm is, in general, much faster. We note that \(X\) can be understood as the sum of \(k\) outcomes of a geometrically distributed experiment with parameter \(p\). Thus, we can use the following sum as a means of generating \(X\):
\[\sum_{j = 1}^k \Biggl\lceil {\frac{\log\ rnd_j}{\log\ q}}\Biggr\rceil \]
A fair coin is tossed until the second time a head turns up. The distribution for the number of tosses is \(u(x, 2, p)\). Thus the probability that \(x\) tosses are needed to obtain two heads is found by letting \(k = 2\) in the above formula. We obtain
\[u(x, 2, 1/2) = {{x-1} \choose 1} \frac 1{2^x}\ ,\] for \(x = 2, 3, \ldots\\).
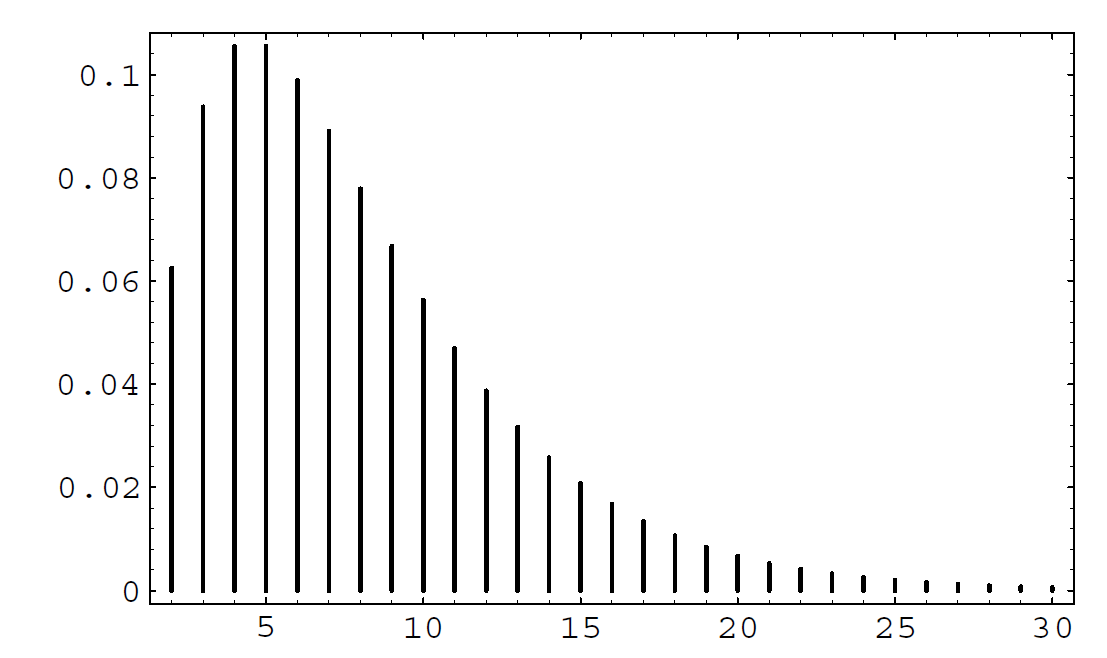
In Figure \(\PageIndex{2}\) we give a graph of the distribution for \(k = 2\) and \(p = .25\). Note that the distribution is quite asymmetric, with a long tail reflecting the fact that large values of \(x\) are possible.
Poisson Distribution
The Poisson distribution arises in many situations. It is safe to say that it is one of the three most important discrete probability distributions (the other two being the uniform and the binomial distributions). The Poisson distribution can be viewed as arising from the binomial distribution or from the exponential density. We shall now explain its connection with the former; its connection with the latter will be explained in the next section.
Suppose that we have a situation in which a certain kind of occurrence happens at random over a period of time. For example, the occurrences that we are interested in might be incoming telephone calls to a police station in a large city. We want to model this situation so that we can consider the probabilities of events such as more than 10 phone calls occurring in a 5-minute time interval. Presumably, in our example, there would be more incoming calls between 6:00 and 7:00 P.M. than between 4:00 and 5:00 A.M., and this fact would certainly affect the above probability. Thus, to have a hope of computing such probabilities, we must assume that the average rate, i.e., the average number of occurrences per minute, is a constant. This rate we will denote by \(\lambda\). (Thus, in a given 5-minute time interval, we would expect about \(5\lambda\) occurrences.) This means that if we were to apply our model to the two time periods given above, we would simply use different rates for the two time periods, thereby obtaining two different probabilities for the given event.
Our next assumption is that the number of occurrences in two non-overlapping time intervals are independent. In our example, this means that the events that there are \(j\) calls between 5:00 and 5:15 P.M. and \(k\) calls between 6:00 and 6:15 P.M. on the same day are independent.
We can use the binomial distribution to model this situation. We imagine that a given time interval is broken up into \(n\) subintervals of equal length. If the subintervals are sufficiently short, we can assume that two or more occurrences happen in one subinterval with a probability which is negligible in comparison with the probability of at most one occurrence. Thus, in each subinterval, we are assuming that there is either 0 or 1 occurrence. This means that the sequence of subintervals can be thought of as a sequence of Bernoulli trials, with a success corresponding to an occurrence in the subinterval.
To decide upon the proper value of \(p\), the probability of an occurrence in a given subinterval, we reason as follows. On the average, there are \(\lambda t\) occurrences in a time interval of length \(t\). If this time interval is divided into \(n\) subintervals, then we would expect, using the Bernoulli trials interpretation, that there should be \(np\) occurrences. Thus, we want \[\lambda t = n p\ ,\] so \[p = {\frac{\lambda t}{n}}\]
We now wish to consider the random variable \(X\), which counts the number of occurrences in a given time interval. We want to calculate the distribution of \(X\). For ease of calculation, we will assume that the time interval is of length 1; for time intervals of arbitrary length \(t\), see Exercise [exer 5.1.26]. We know that \[P(X = 0) = b(n, p, 0) = (1 - p)^n = \Bigl(1 - {\lambda \over n}\Bigr)^n\ .\] For large \(n\), this is approximately \(e^{-\lambda}\). It is easy to calculate that for any fixed \(k\), we have
\[{\frac{b(n, p, k)}{b(n, p, k-1)}} = {\frac{\lambda - (k-1)p}{kq}}\]
which, for large \(n\) (and therefore small \(p\)) is approximately \(\lambda/k\). Thus, we have
\[P(X = 1) \approx \lambda e^{-\lambda},\]
and in general, \[P(X = k) \approx {\frac{\lambda^k}{k!}} e^{-\lambda} \]
The above distribution is the Poisson distribution. We note that it must be checked that the distribution given in Equation 5.1 really is a distribution, i.e., that its values are non-negative and sum to 1. (See Exercise 5.1.27.)
The Poisson distribution is used as an approximation to the binomial distribution when the parameters \(n\) and \(p\) are large and small, respectively (see Examples 5.1.3 and 5.1.5). However, the Poisson distribution also arises in situations where it may not be easy to interpret or measure the parameters \(n\) and \(p\) (see Example 5.5.5.
A typesetter makes, on the average, one mistake per 1000 words. Assume that he is setting a book with 100 words to a page. Let \(S_{100}\) be the number of mistakes that he makes on a single page. Then the exact probability distribution for \(S_{100}\) would be obtained by considering \(S_{100}\) as a result of 100 Bernoulli trials with \(p = 1/1000\). The expected value of \(S_{100}\) is \(\lambda = 100(1/1000) = .1\). The exact probability that \(S_{100} = j\) is \(b(100,1/1000,j)\), and the Poisson approximation is
\[\frac {e^{-.1}(.1)^j}{j!}.\]
In Table \(\PageIndex{1}\) we give, for various values of \(n\) and \(p\), the exact values computed by the binomial distribution and the Poisson approximation.
| Poisson | Binomial | Poisson | Binomial | Poisson | Binomial | |
| \(n = 100\) | \(n = 100\) | \(n = 1000\) | ||||
| \(j\) | \(\lambda = .1\) | \(p = .001\) | \(\lambda = 1\) | \(p = .01\) | \(\lambda = 10\) | \(p = .01\) |
| 0 | .9048 | .9048 | .3679 | .3660 | .0000 | .0000 |
| 1 | .0905 | .0905 | .3679 | .3697 | .0005 | .0004 |
| 2 | .0045 | .0045 | .1839 | .1849 | .0023 | .0022 |
| 3 | .0002 | .0002 | .0613 | .0610 | .0076 | .0074 |
| 4 | .0000 | .0000 | .0153 | .0149 | .0189 | .0186 |
| 5 | .0031 | .0029 | .0378 | .0374 | ||
| 6 | .0005 | .0005 | .0631 | .0627 | ||
| 7 | .0001 | .0001 | .0901 | .0900 | ||
| 8 | .0000 | .0000 | .1126 | .1128 | ||
| 9 | .1251 | .1256 | ||||
| 10 | .1251 | .1257 | ||||
| 11 | .1137 | .1143 | ||||
| 12 | .0948 | .0952 | ||||
| 13 | .0729 | .0731 | ||||
| 14 | .0521 | .0520 | ||||
| 15 | .0347 | .0345 | ||||
| 16 | .0217 | .0215 | ||||
| 17 | .0128 | .0126 | ||||
| 18 | .0071 | .0069 | ||||
| 19 | .0037 | .0036 | ||||
| 20 | .0019 | .0018 | ||||
| 21 | .0009 | .0009 | ||||
| 22 | .0004 | .0004 | ||||
| 23 | .0002 | .0002 | ||||
| 24 | .0001 | .0001 | ||||
| 25 | .0000 | .0000 |
In his book,1 Feller discusses the statistics of flying bomb hits in the south of London during the Second World War.
Assume that you live in a district of size 10 blocks by 10 blocks so that the total district is divided into 100 small squares. How likely is it that the square in which you live will receive no hits if the total area is hit by 400 bombs?
We assume that a particular bomb will hit your square with probability 1/100. Since there are 400 bombs, we can regard the number of hits that your square receives as the number of in a Bernoulli trials process with \(n = 400\) and \(p = 1/100\). Thus we can use the Poisson distribution with \(\lambda = 400 \cdot 1/100 = 4\) to approximate the probability that your square will receive \(j\) hits. This probability is \(p(j) = e^{-4} 4^j/j!\). The expected number of squares that receive exactly \(j\) hits is then \(100 \cdot p(j)\). It is easy to write a program LondonBombs to simulate this situation and compare the expected number of squares with \(j\) hits with the observed number. In Exercise 9.2.15 you are asked to compare the actual observed data with that predicted by the Poisson distribution.

In Figure \(\PageIndex{3}\), we have shown the simulated hits, together with a spike graph showing both the observed and predicted frequencies. The observed frequencies are shown as squares, and the predicted frequencies are shown as dots.
If the reader would rather not consider flying bombs, he is invited to instead consider an analogous situation involving cookies and raisins. We assume that we have made enough cookie dough for 500 cookies. We put 600 raisins in the dough, and mix it thoroughly. One way to look at this situation is that we have 500 cookies, and after placing the cookies in a grid on the table, we throw 600 raisins at the cookies. (See Exercise \(\PageIndex{29}\).)
Suppose that in a certain fixed amount \(A\) of blood, the average human has 40 white blood cells. Let \(X\) be the random variable which gives the number of white blood cells in a random sample of size \(A\) from a random individual. We can think of \(X\) as binomially distributed with each white blood cell in the body representing a trial. If a given white blood cell turns up in the sample, then the trial corresponding to that blood cell was a success. Then \(p\) should be taken as the ratio of \(A\) to the total amount of blood in the individual, and \(n\) will be the number of white blood cells in the individual. Of course, in practice, neither of these parameters is very easy to measure accurately, but presumably the number 40 is easy to measure. But for the average human, we then have \(40 = np\), so we can think of \(X\) as being Poisson distributed, with parameter \(\lambda = 40\). In this case, it is easier to model the situation using the Poisson distribution than the binomial distribution.
To simulate a Poisson random variable on a computer, a good way is to take advantage of the relationship between the Poisson distribution and the exponential density. This relationship and the resulting simulation algorithm will be described in the next section.
Hypergeometric Distribution
Suppose that we have a set of \(N\) balls, of which \(k\) are red and \(N-k\) are blue. We choose \(n\) of these balls, without replacement, and define \(X\) to be the number of red balls in our sample. The distribution of \(X\) is called the hypergeometric distribution. We note that this distribution depends upon three parameters, namely \(N\), \(k\), and \(n\). There does not seem to be a standard notation for this distribution; we will use the notation \(h(N, k, n, x)\) to denote \(P(X = x)\). This probability can be found by noting that there are \[{N \choose n}\] different samples of size \(n\), and the number of such samples with exactly \(x\) red balls is obtained by multiplying the number of ways of choosing \(x\) red balls from the set of \(k\) red balls and the number of ways of choosing \(n-x\) blue balls from the set of \(N-k\) blue balls. Hence, we have
\[h(N, k, n, x) = \frac{\binom{k}{x}\binom{N-k}{n-x}}{\binom{N}{n}} \]
This distribution can be generalized to the case where there are more than two types of objects. (See Exercise 5.1.24.)
If we let \(N\) and \(k\) tend to \(\infty\), in such a way that the ratio \(k/N\) remains fixed, then the hypergeometric distribution tends to the binomial distribution with parameters \(n\) and \(p = k/N\). This is reasonable because if \(N\) and \(k\) are much larger than \(n\), then whether we choose our sample with or without replacement should not affect the probabilities very much, and the experiment consisting of choosing with replacement yields a binomially distributed random variable (see Exercise 5.1.124).
An example of how this distribution might be used is given in Exercises 5.1.21 and 5.1.22. We now give another example involving the hypergeometric distribution. It illustrates a statistical test called Fisher’s Exact Test.
It is often of interest to consider two traits, such as eye color and hair color, and to ask whether there is an association between the two traits. Two traits are associated if knowing the value of one of the traits for a given person allows us to predict the value of the other trait for that person. The stronger the association, the more accurate the predictions become. If there is no association between the traits, then we say that the traits are independent. In this example, we will use the traits of gender and political party, and we will assume that there are only two possible genders, female and male, and only two possible political parties, Democratic and Republican.
Suppose that we have collected data concerning these traits. To test whether there is an association between the traits, we first assume that there is no association between the two traits. This gives rise to an “expected" data set, in which knowledge of the value of one trait is of no help in predicting the value of the other trait. Our collected data set usually differs from this expected data set. If it differs by quite a bit, then we would tend to reject the assumption of independence of the traits. To nail down what is meant by “quite a bit," we decide which possible data sets differ from the expected data set by at least as much as ours does, and then we compute the probability that any of these data sets would occur under the assumption of independence of traits. If this probability is small, then it is unlikely that the difference between our collected data set and the expected data set is due entirely to chance.
Suppose that we have collected the data shown in Table .
|
Democrat |
Republican |
||
|---|---|---|---|
|
Female |
24 |
4 |
28 |
|
Male |
8 |
14 |
22 |
| 32 | 18 |
50 |
The row and column sums are called marginal totals, or marginals. In what follows, we will denote the row sums by \(t_{11}\) and \(t_{12}\), and the column sums by \(t_{21}\) and \(t_{22}\). The \(ij\)th entry in the table will be denoted by \(s_{ij}\). Finally, the size of the data set will be denoted by \(n\). Thus, a general data table will look as shown in Table .
|
Democrat |
Republican |
||
|---|---|---|---|
|
Female |
\(s_{11}\) | \(s_{12}\) |
\(t_{11}\) |
|
Male |
\(s_{21}\) | \(s_{22}\) |
\(t_{12}\) |
| \(t_{21}\) | \(t_{22}\) |
\(n\) |
We now explain the model which will be used to construct the “expected" data set. In the model, we assume that the two traits are independent. We then put \(t_{21}\) yellow balls and \(t_{22}\) green balls, corresponding to the Democratic and Republican marginals, into an urn. We draw \(t_{11}\) balls, without replacement, from the urn, and call these balls females. The \(t_{12}\) balls remaining in the urn are called males. In the specific case under consideration, the probability of getting the actual data under this model is given by the expression
\[\frac{\binom{32}{24}\binom{18}{4}}{\binom{50}{28}} \]
i.e., a value of the hypergeometric distribution.
We are now ready to construct the expected data set. If we choose 28 balls out of 50, we should expect to see, on the average, the same percentage of yellow balls in our sample as in the urn. Thus, we should expect to see, on the average, \(28(32/50) = 17.92 \approx 18\) yellow balls in our sample. (See Exercise .) The other expected values are computed in exactly the same way. Thus, the expected data set is shown in Table .
|
Democrat |
Republican |
||
|---|---|---|---|
|
Female |
18 | 10 |
28 |
|
Male |
14 |
8 |
22 |
| 32 | 18 |
50 |
We note that the value of \(s_{11}\) determines the other three values in the table, since the marginals are all fixed. Thus, in considering the possible data sets that could appear in this model, it is enough to consider the various possible values of \(s_{11}\). In the specific case at hand, what is the probability of drawing exactly \(a\) yellow balls, i.e., what is the probability that \(s_{11} = a\)? It is
\[ \frac{\binom{32}{a}\binom{18}{28-a}}{\binom{50}{28}}\]
We are now ready to decide whether our actual data differs from the expected data set by an amount which is greater than could be reasonably attributed to chance alone. We note that the expected number of female Democrats is 18, but the actual number in our data is 24. The other data sets which differ from the expected data set by more than ours correspond to those where the number of female Democrats equals 25, 26, 27, or 28. Thus, to obtain the required probability, we sum the expression in (5.3) from \(a = 24\) to \(a = 28\). We obtain a value of \(.000395\). Thus, we should reject the hypothesis that the two traits are independent.
Finally, we turn to the question of how to simulate a hypergeometric random variable \(X\). Let us assume that the parameters for \(X\) are \(N\), \(k\), and \(n\). We imagine that we have a set of \(N\) balls, labelled from 1 to \(N\). We decree that the first \(k\) of these balls are red, and the rest are blue. Suppose that we have chosen \(m\) balls, and that \(j\) of them are red. Then there are \(k-j\) red balls left, and \(N-m\) balls left. Thus, our next choice will be red with probability
\[\frac{k-j}{N-m}\]
So at this stage, we choose a random number in \([0, 1]\), and report that a red ball has been chosen if and only if the random number does not exceed the above expression. Then we update the values of \(m\) and \(j\), and continue until \(n\) balls have been chosen.
Benford Distribution
Our next example of a distribution comes from the study of leading digits in data sets. It turns out that many data sets that occur “in real life" have the property that the first digits of the data are not uniformly distributed over the set \(\{1, 2, \ldots, 9\}\). Rather, it appears that the digit 1 is most likely to occur, and that the distribution is monotonically decreasing on the set of possible digits. The Benford distribution appears, in many cases, to fit such data. Many explanations have been given for the occurrence of this distribution. Possibly the most convincing explanation is that this distribution is the only one that is invariant under a change of scale. If one thinks of certain data sets as somehow “naturally occurring," then the distribution should be unaffected by which units are chosen in which to represent the data, i.e., the distribution should be invariant under change of scale.
Theodore Hill2 gives a general description of the Benford distribution, when one considers the first \(d\) digits of integers in a data set. We will restrict our attention to the first digit. In this case, the Benford distribution has distribution function \[f(k) = \log_{10}(k+1) - \log_{10}(k)\ ,\] for \(1 \le k \le 9\).
Mark Nigrini3 has advocated the use of the Benford distribution as a means of testing suspicious financial records such as bookkeeping entries, checks, and tax returns. His idea is that if someone were to “make up" numbers in these cases, the person would probably produce numbers that are fairly uniformly distributed, while if one were to use the actual numbers, the leading digits would roughly follow the Benford distribution. As an example, Nigrini analyzed President Clinton’s tax returns for a 13-year period. In Figure 5.1.4, the Benford distribution values are shown as squares, and the President’s tax return data are shown as circles. One sees that in this example, the Benford distribution fits the data very well.

This distribution was discovered by the astronomer Simon Newcomb who stated the following in his paper on the subject: “That the ten digits do not occur with equal frequency must be evident to anyone making use of logarithm tables, and noticing how much faster the first pages wear out than the last ones. The first significant figure is oftener 1 than any other digit, and the frequency diminishes up to 9."4
Exercises
Exercise \(\PageIndex{1}\)
For which of the following random variables would it be appropriate to assign a uniform distribution?
- Let \(X\) represent the roll of one die.
- Let \(X\) represent the number of heads obtained in three tosses of a coin.
- A roulette wheel has 38 possible outcomes: 0, 00, and 1 through 36. Let \(X\) represent the outcome when a roulette wheel is spun.
- Let \(X\) represent the birthday of a randomly chosen person.
- Let \(X\) represent the number of tosses of a coin necessary to achieve a head for the first time.
Exercise \(\PageIndex{2}\)
Let \(n\) be a positive integer. Let \(S\) be the set of integers between 1 and \(n\). Consider the following process: We remove a number from \(S\) at random and write it down. We repeat this until \(S\) is empty. The result is a permutation of the integers from 1 to \(n\). Let \(X\) denote this permutation. Is \(X\) uniformly distributed?
Exercise \(\PageIndex{3}\)
Let \(X\) be a random variable which can take on countably many values. Show that \(X\) cannot be uniformly distributed.
Exercise \(\PageIndex{4}\)
Suppose we are attending a college which has 3000 students. We wish to choose a subset of size 100 from the student body. Let \(X\) represent the subset, chosen using the following possible strategies. For which strategies would it be appropriate to assign the uniform distribution to \(X\)? If it is appropriate, what probability should we assign to each outcome?
- Take the first 100 students who enter the cafeteria to eat lunch.
- Ask the Registrar to sort the students by their Social Security number, and then take the first 100 in the resulting list.
- Ask the Registrar for a set of cards, with each card containing the name of exactly one student, and with each student appearing on exactly one card. Throw the cards out of a third-story window, then walk outside and pick up the first 100 cards that you find.
Exercise \(\PageIndex{5}\)
Under the same conditions as in the preceding exercise, can you describe a procedure which, if used, would produce each possible outcome with the same probability? Can you describe such a procedure that does not rely on a computer or a calculator?
Exercise \(\PageIndex{6}\)
Let \(X_1,\ X_2,\ \ldots,\ X_n\) be \(n\) mutually independent random variables, each of which is uniformly distributed on the integers from 1 to \(k\). Let \(Y\) denote the minimum of the \(X_i\)’s. Find the distribution of \(Y\).
Exercise \(\PageIndex{7}\)
A die is rolled until the first time \(T\) that a six turns up.
- What is the probability distribution for \(T\)?
- Find \(P(T > 3)\).
- Find \(P(T > 6 | T > 3)\).
Exercise \(\PageIndex{8}\)
If a coin is tossed a sequence of times, what is the probability that the first head will occur after the fifth toss, given that it has not occurred in the first two tosses?
Exercise \(\PageIndex{9}\)
A worker for the Department of Fish and Game is assigned the job of estimating the number of trout in a certain lake of modest size. She proceeds as follows: She catches 100 trout, tags each of them, and puts them back in the lake. One month later, she catches 100 more trout, and notes that 10 of them have tags.
- Without doing any fancy calculations, give a rough estimate of the number of trout in the lake.
- Let \(N\) be the number of trout in the lake. Find an expression, in terms of \(N\), for the probability that the worker would catch 10 tagged trout out of the 100 trout that she caught the second time.
- Find the value of \(N\) which maximizes the expression in part (b). This value is called the for the unknown quantity \(N\). : Consider the ratio of the expressions for successive values of \(N\).
Exercise \(\PageIndex{10}\)
A census in the United States is an attempt to count everyone in the country. It is inevitable that many people are not counted. The U. S. Census Bureau proposed a way to estimate the number of people who were not counted by the latest census. Their proposal was as follows: In a given locality, let \(N\) denote the actual number of people who live there. Assume that the census counted \(n_1\) people living in this area. Now, another census was taken in the locality, and \(n_2\) people were counted. In addition, \(n_{12}\) people were counted both times.
- Given \(N\), \(n_1\), and \(n_2\), let \(X\) denote the number of people counted both times. Find the probability that \(X = k\), where \(k\) is a fixed positive integer between 0 and \(n_2\).
- Now assume that \(X = n_{12}\). Find the value of \(N\) which maximizes the expression in part (a). : Consider the ratio of the expressions for successive values of \(N\).
Exercise \(\PageIndex{11}\)
Suppose that \(X\) is a random variable which represents the number of calls coming in to a police station in a one-minute interval. In the text, we showed that \(X\) could be modelled using a Poisson distribution with parameter \(\lambda\), where this parameter represents the average number of incoming calls per minute. Now suppose that \(Y\) is a random variable which represents the number of incoming calls in an interval of length \(t\). Show that the distribution of \(Y\) is given by
\(P(Y=k)=e^{-\lambda t} \frac{(\lambda t)^k}{k !}\),
i.e., \(Y\) is Poisson with parameter \(\lambda t\).
Hint: Suppose a Martian were to observe the police station. Let us also assume that the basic time interval used on Mars is exactly \(t\) Earth minutes. Finally, we will assume that the Martian understands the derivation of the Poisson distribution in the text. What would she write down for the distribution of \(Y\)?
Exercise \(PageIndex{12}\)
Show that the values of the Poisson distribution given in Equation [eq 5.1] sum to 1.
Exercise \(\PageIndex{13}\)
The Poisson distribution with parameter \(\lambda = .3\) has been assigned for the outcome of an experiment. Let \(X\) be the outcome function. Find \(P(X = 0)\), \(P(X = 1)\), and \(P(X > 1)\).
Exercise \(\PageIndex{14}\)
On the average, only 1 person in 1000 has a particular rare blood type.
- Find the probability that, in a city of 10,000 people, no one has this blood type.
- How many people would have to be tested to give a probability greater than 1/2 of finding at least one person with this blood type?
Exercise \(\PageIndex{15}\)
Write a program for the user to input \(n\), \(p\), \(j\) and have the program print out the exact value of \(b(n, p, k)\) and the Poisson approximation to this value.
Exercise \(\PageIndex{16}\)
Assume that, during each second, a Dartmouth switchboard receives one call with probability .01 and no calls with probability .99. Use the Poisson approximation to estimate the probability that the operator will miss at most one call if she takes a 5-minute coffee break.
Exercise \(\PageIndex{17}\)
The probability of a royal flush in a poker hand is \(p = 1/649{,}740\). How large must \(n\) be to render the probability of having no royal flush in \(n\) hands smaller than \(1/e\)?
Exercise \(\PageIndex{18}\)
A baker blends 600 raisins and 400 chocolate chips into a dough mix and, from this, makes 500 cookies.
- Find the probability that a randomly picked cookie will have no raisins.
- Find the probability that a randomly picked cookie will have exactly two chocolate chips.
- Find the probability that a randomly chosen cookie will have at least two bits (raisins or chips) in it.
Exercise \(\PageIndex{19}\)
The probability that, in a bridge deal, one of the four hands has all hearts is approximately \(6.3 \times 10^{-12}\). In a city with about 50,000 bridge players the resident probability expert is called on the average once a year (usually late at night) and told that the caller has just been dealt a hand of all hearts. Should she suspect that some of these callers are the victims of practical jokes?
Exercise \(\PageIndex{20}\)
An advertiser drops 10,000 leaflets on a city which has 2000 blocks. Assume that each leaflet has an equal chance of landing on each block. What is the probability that a particular block will receive no leaflets?
Exercise \(\PageIndex{21}\)
In a class of 80 students, the professor calls on 1 student chosen at random for a recitation in each class period. There are 32 class periods in a term.
- Write a formula for the exact probability that a given student is called upon \(j\) times during the term.
- Write a formula for the Poisson approximation for this probability. Using your formula estimate the probability that a given student is called upon more than twice.
Exercise \(\PageIndex{22}\)
Assume that we are making raisin cookies. We put a box of 600 raisins into our dough mix, mix up the dough, then make from the dough 500 cookies. We then ask for the probability that a randomly chosen cookie will have 0, 1, 2, … raisins. Consider the cookies as trials in an experiment, and let \(X\) be the random variable which gives the number of raisins in a given cookie. Then we can regard the number of raisins in a cookie as the result of \(n = 600\) independent trials with probability \(p = 1/500\) for success on each trial. Since \(n\) is large and \(p\) is small, we can use the Poisson approximation with \(\lambda = 600(1/500) = 1.2\). Determine the probability that a given cookie will have at least five raisins.
Exercise \(\PageIndex{23}\)
For a certain experiment, the Poisson distribution with parameter \(\lambda = m\) has been assigned. Show that a most probable outcome for the experiment is the integer value \(k\) such that \(m - 1 \leq k \leq m\). Under what conditions will there be two most probable values? : Consider the ratio of successive probabilities.
Exercise \(\PageIndex{24}\)
When John Kemeny was chair of the Mathematics Department at Dartmouth College, he received an average of ten letters each day. On a certain weekday he received no mail and wondered if it was a holiday. To decide this he computed the probability that, in ten years, he would have at least 1 day without any mail. He assumed that the number of letters he received on a given day has a Poisson distribution. What probability did he find? : Apply the Poisson distribution twice. First, to find the probability that, in 3000 days, he will have at least 1 day without mail, assuming each year has about 300 days on which mail is delivered.
Exercise \(\PageIndex{25}\)
Reese Prosser never puts money in a 10-cent parking meter in Hanover. He assumes that there is a probability of .05 that he will be caught. The first offense costs nothing, the second costs 2 dollars, and subsequent offenses cost 5 dollars each. Under his assumptions, how does the expected cost of parking 100 times without paying the meter compare with the cost of paying the meter each time?
Exercise \(\PageIndex{26}\)
Feller5 discusses the statistics of flying bomb hits in an area in the south of London during the Second World War. The area in question was divided into \(24 \times 24 = 576\) small areas. The total number of hits was 537. There were 229 squares with 0 hits, 211 with 1 hit, 93 with 2 hits, 35 with 3 hits, 7 with 4 hits, and 1 with 5 or more. Assuming the hits were purely random, use the Poisson approximation to find the probability that a particular square would have exactly \(k\) hits. Compute the expected number of squares that would have 0, 1, 2, 3, 4, and 5 or more hits and compare this with the observed results.
Exercise \(\PageIndex{27}\)
Assume that the probability that there is a significant accident in a nuclear power plant during one year’s time is .001. If a country has 100 nuclear plants, estimate the probability that there is at least one such accident during a given year.
Exercise \(\PageIndex{28}\)
An airline finds that 4 percent of the passengers that make reservations on a particular flight will not show up. Consequently, their policy is to sell 100 reserved seats on a plane that has only 98 seats. Find the probability that every person who shows up for the flight will find a seat available.
Exercise \(\PageIndex{29}\)
The king’s coinmaster boxes his coins 500 to a box and puts 1 counterfeit coin in each box. The king is suspicious, but, instead of testing all the coins in 1 box, he tests 1 coin chosen at random out of each of 500 boxes. What is the probability that he finds at least one fake? What is it if the king tests 2 coins from each of 250 boxes?
Exercise \(PageIndex{30}\)
(From Kemeny6) Show that, if you make 100 bets on the number 17 at roulette at Monte Carlo (see Example 6.1.13), you will have a probability greater than 1/2 of coming out ahead. What is your expected winning?
Exercise \(\PageIndex{31}\)
In one of the first studies of the Poisson distribution, von Bortkiewicz7 considered the frequency of deaths from kicks in the Prussian army corps. From the study of 14 corps over a 20-year period, he obtained the data shown in Table \(\PageIndex{5}\)
| Number of deaths | Number of corps with \(x\) deaths in a given year |
|---|---|
| 0 | 144 |
| 1 |
91 |
| 2 |
32 |
| 3 |
11 |
| 4 |
2 |
Fit a Poisson distribution to this data and see if you think that the Poisson distribution is appropriate.
Exercise \(\PageIndex{32}\)
It is often assumed that the auto traffic that arrives at the intersection during a unit time period has a Poisson distribution with expected value \(m\). Assume that the number of cars \(X\) that arrive at an intersection from the north in unit time has a Poisson distribution with parameter \(\lambda = m\) and the number \(Y\) that arrive from the west in unit time has a Poisson distribution with parameter \(\lambda = \bar m\). If \(X\) and \(Y\) are independent, show that the total number \(X + Y\) that arrive at the intersection in unit time has a Poisson distribution with parameter \(\lambda = m + \bar m\).
Exercise \(\PageIndex{33}\)
Cars coming along Magnolia Street come to a fork in the road and have to choose either Willow Street or Main Street to continue. Assume that the number of cars that arrive at the fork in unit time has a Poisson distribution with parameter \(\lambda = 4\). A car arriving at the fork chooses Main Street with probability 3/4 and Willow Street with probability 1/4. Let \(X\) be the random variable which counts the number of cars that, in a given unit of time, pass by Joe’s Barber Shop on Main Street. What is the distribution of \(X\)?
Exercise \(\PageIndex{34}\)
In the appeal of the People v. Collins case (see Exercise 4.1.28), the counsel for the defense argued as follows: Suppose, for example, there are 5,000,000 couples in the Los Angeles area and the probability that a randomly chosen couple fits the witnesses’ description is 1/12,000,000. Then the probability that there are two such couples given that there is at least one is not at all small. Find this probability. (The California Supreme Court overturned the initial guilty verdict.)
Exercise \(\PageIndex{35}\)
A manufactured lot of brass turnbuckles has \(S\) items of which \(D\) are defective. A sample of \(s\) items is drawn without replacement. Let \(X\) be a random variable that gives the number of defective items in the sample. Let \(p(d) = P(X = d)\).
- Show that \[p(d) = \frac{\binom{D}{d}\binom{S-D}{s-d}}{\binom{S}{s}}\ .\] Thus, X is hypergeometric.
- Prove the following identity, known as Euler's Formula: \[\sum_{d = 0}^{\min(D,s)}\binom{D}{d}\binom{S-D}{s-d} = \binom{S}{s}}\ .\]
Exercise \(\PageIndex{36}\)
A bin of 1000 turnbuckles has an unknown number \(D\) of defectives. A sample of 100 turnbuckles has 2 defectives. The for \(D\) is the number of defectives which gives the highest probability for obtaining the number of defectives observed in the sample. Guess this number \(D\) and then write a computer program to verify your guess.
Exercise \(\PageIndex{37}\)
There are an unknown number of moose on Isle Royale (a National Park in Lake Superior). To estimate the number of moose, 50 moose are captured and tagged. Six months later 200 moose are captured and it is found that 8 of these were tagged. Estimate the number of moose on Isle Royale from these data, and then verify your guess by computer program (see Exercise 5.1.36).
Exercise \(\PageIndex{38}\)
A manufactured lot of buggy whips has 20 items, of which 5 are defective. A random sample of 5 items is chosen to be inspected. Find the probability that the sample contains exactly one defective item
- if the sampling is done with replacement.
- if the sampling is done without replacement.
Exercise \(\PageIndex{39}\)
Suppose that \(N\) and \(k\) tend to \(\infty\) in such a way that \(k/N\) remains fixed. Show that \[h(N, k, n, x) \rightarrow b(n, k/N, x)\ .\]
Exercise \(\PageIndex{40}\)
A bridge deck has 52 cards with 13 cards in each of four suits: spades, hearts, diamonds, and clubs. A hand of 13 cards is dealt from a shuffled deck. Find the probability that the hand has
- a distribution of suits 4, 4, 3, 2 (for example, four spades, four hearts, three diamonds, two clubs).
- a distrbution of suits 5, 3, 3, 2.
Exercise \(PageIndex{41}\)
Write a computer algorithm that simulates a hypergeometric random variable with parameters \(N\), \(k\), and \(n\).
Exercise \(\PageIndex{42}\)
You are presented with four different dice. The first one has two sides marked 0 and four sides marked 4. The second one has a 3 on every side. The third one has a 2 on four sides and a 6 on two sides, and the fourth one has a 1 on three sides and a 5 on three sides. You allow your friend to pick any of the four dice he wishes. Then you pick one of the remaining three and you each roll your die. The person with the largest number showing wins a dollar. Show that you can choose your die so that you have probability 2/3 of winning no matter which die your friend picks. (See Tenney and Foster.8)
Exercise \(\PageIndex{43}\)
The students in a certain class were classified by hair color and eye color. The conventions used were: Brown and black hair were considered dark, and red and blonde hair were considered light; black and brown eyes were considered dark, and blue and green eyes were considered light. They collected the data shown in Table \(\PageIndex{6}\)
| Dark Eyes | Light Eyes | ||
|---|---|---|---|
| Dark Hair | 28 | 15 |
43 |
| Light Hair |
9 |
23 |
32 |
| 37 | 38 |
75 |
Are these traits independent? (See Example \(\PageIndex{6}\).)
Exercise \(\PageIndex{44}\)
Suppose that in the hypergeometric distribution, we let \(N\) and \(k\) tend to \(\infty\) in such a way that the ratio \(k/N\) approaches a real number \(p\) between 0 and 1. Show that the hypergeometric distribution tends to the binomial distribution with parameters \(n\) and \(p\).
Exercise \(\PageIndex{45}\)
- Compute the leading digits of the first 100 powers of 2, and see how well these data fit the Benford distribution.
- Multiply each number in the data set of part (a) by 3, and compare the distribution of the leading digits with the Benford distribution.
Exercise \(\PageIndex{46}\)
In the Powerball lottery, contestants pick 5 different integers between 1 and 45, and in addition, pick a bonus integer from the same range (the bonus integer can equal one of the first five integers chosen). Some contestants choose the numbers themselves, and others let the computer choose the numbers. The data shown in Table \(\PageIndex{7}\) are the contestant-chosen numbers in a certain state on May 3, 1996. A spike graph of the data is shown in Figure \(\PageIndex{5}\)
| Integer | Times | Integer | Times | Integer | Times |
| Chosen | Chosen | Chosen | |||
| 1 | 2646 | 2 | 2934 | 3 | 3352 |
| 4 | 3000 | 5 | 3357 | 6 | 2892 |
| 7 | 3657 | 8 | 3025 | 9 | 3362 |
| 10 | 2985 | 11 | 3138 | 12 | 3043 |
| 13 | 2690 | 14 | 2423 | 15 | 2556 |
| 16 | 2456 | 17 | 2479 | 18 | 2276 |
| 19 | 2304 | 20 | 1971 | 21 | 2543 |
| 22 | 2678 | 23 | 2729 | 24 | 2414 |
| 25 | 2616 | 26 | 2426 | 27 | 2381 |
| 28 | 2059 | 29 | 2039 | 30 | 2298 |
| 31 | 2081 | 32 | 1508 | 33 | 1887 |
| 34 | 1463 | 35 | 1594 | 36 | 1354 |
| 37 | 1049 | 38 | 1165 | 39 | 1248 |
| 40 | 1493 | 41 | 1322 | 42 | 1423 |
| 43 | 1207 | 44 | 1259 | 45 | 1224 |



