3.8: Interpreting Standard Deviations
- Page ID
- 17991
Figure \(\PageIndex{1}\) shows two symmerical distributions. The frequency distribution on the left (red) has a mean of 40 and a standard deviation of 5; the frequency distribution on the right (blue) has a mean of 60 and a standard deviation of 10. For the tall and narrow distribution on the left, 68% of the distribution is between 45 and 55; for the shorter distribution on the right, 68% is between 50 and 70. Notice that as the standard deviation gets smaller, the distribution becomes much narrower, regardless of where the center of the distribution (mean) is. Figure \(\PageIndex{2}\) presents several more examples of this effect, discussed below.
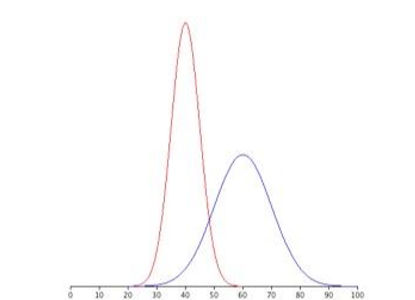
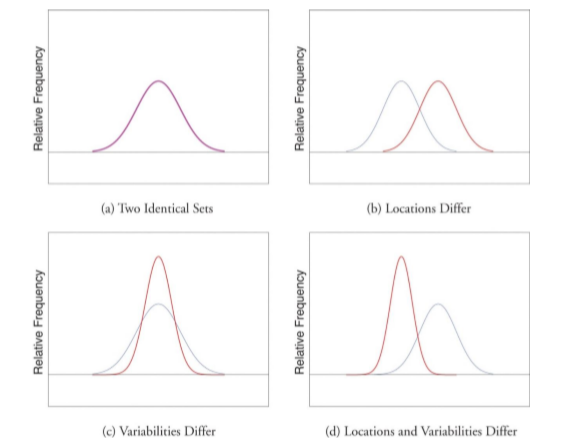
Figure \(\PageIndex{2}\) was Figure 3.8.3 from the Introduction to Measures of Variability. In Figure \(\PageIndex{2}\) Panel (a), the mean and standard deviations are both the same. You can see where the name “bell curve” comes from: it looks a bit like a bell. In Panel (b), the mean of one of the distributions of data (red, on the right) is higher then the mean of the other distribution (blue, on the left) but the standard deviations are the same because they are the same shape. these distributions have the same “width”. The only difference between them is that they’ve been shifted to the left or to the right. In every other respect they’re identical. In contrast, if we increase the standard deviation while keeping the mean constant, the peak of the distribution stays in the same place, but the distribution gets taller, as you can see in Panel (c); the means are the same (because the center of both distributions are in the same place on the x-axis), but one standard deviation is smaller (red, tall and narrow) then the other standard deviation (blue, bell shaped). The smaller standard deviation tells us that the scores, on average, are close to the mean. Notice, though, that when a distribution gets taller, the width shrinks (it gets more narrow). Finally, Panel (d) shows two distributions of data in which the means and the standard deviations are different.
Contributors
Foster et al. (University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus)


