3.7: Variance of Discrete Random Variables
- Page ID
- 4373
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We now look at our second numerical characteristic associated to random variables.
Definition \(\PageIndex{1}\)
The variance of a random variable \(X\) is given by
$$\sigma^2 = \text{Var}(X) = \text{E}[(X-\mu)^2],\notag$$
where \(\mu\) denotes the expected value of \(X\). The standard deviation of \(X\) is given by
$$\sigma = \text{SD}(X) = \sqrt{\text{Var}(X)}.\notag$$
In words, the variance of a random variable is the average of the squared deviations of the random variable from its mean (expected value). Notice that the variance of a random variable will result in a number with units squared, but the standard deviation will have the same units as the random variable. Thus, the standard deviation is easier to interpret, which is why we make a point to define it.
The variance and standard deviation give us a measure of spread for random variables. The standard deviation is interpreted as a measure of how "spread out'' the possible values of \(X\) are with respect to the mean of \(X\), \(\mu = \text{E}[X]\).
Example \(\PageIndex{1}\)
Consider the two random variables \(X_1\) and \(X_2\), whose probability mass functions are given by the histograms in Figure 1 below. Note that \(X_1\) and \(X_2\) have the same mean. However, in looking at the histograms, we see that the possible values of \(X_2\) are more "spread out" from the mean, indicating that the variance (and standard deviation) of \(X_2\) is larger.
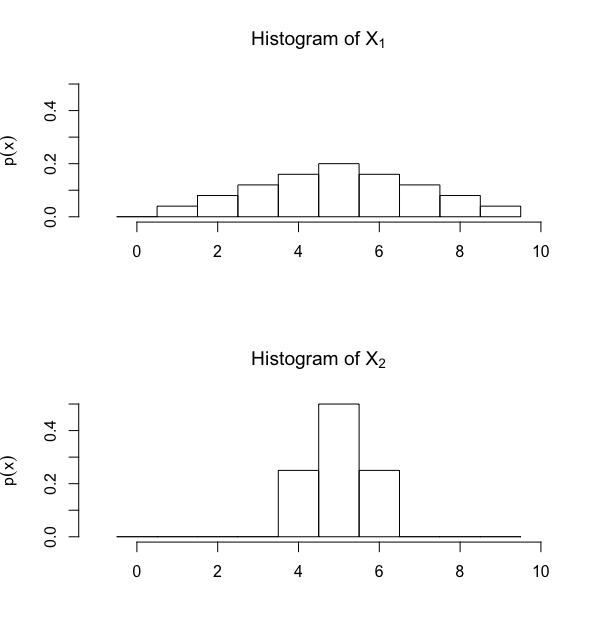
Figure 1: Histograms for random variables \(X_1\) and \(X_2\), both with same expected value different variance.
Theorem 3.6.1 actually tells us how to compute variance, since it is given by finding the expected value of a function applied to the random variable. First, if \(X\) is a discrete random variable with possible values \(x_1, x_2, \ldots, x_i, \ldots\), and probability mass function \(p(x)\), then the variance of \(X\) is given by
$$\text{Var}(X) = \sum_{i} (x_i - \mu)^2\cdot p(x_i).\notag$$
The above formula follows directly from Definition 3.7.1. However, there is an alternate formula for calculating variance, given by the following theorem, that is often easier to use.
Theorem \(\PageIndex{1}\)
Let \(X\) be any random variable, with mean \(\mu\). Then the variance of \(X\) is
$$\text{Var}(X) = \text{E}[X^2] - \mu^2.$$
- Proof
-
By the definition of variance (Definition 3.7.1) and the linearity of expectation, we have the following:
\begin{align*}
\text{Var}(X)&= \text{E}[(X-\mu)^2]\\
&= \text{E}[X^2+\mu^2-2X\mu]\\
&= \text{E}[X^2]+\text{E}[\mu^2]-\text{E}[2X\mu]\\
&= \text{E}[X^2] + \mu^2-2\mu \text{E}[X] \quad (\text{Note: since}\ \mu\ \text{is constant, we can take it out from the expected value})\\
&= \text{E}[X^2] + \mu^2-2\mu^2\\
&= \text{E}[X^2] -\mu^2
\end{align*}
Example \(\PageIndex{2}\)
Continuing in the context of Example 3.6.1, we calculate the variance and standard deviation of the random variable \(X\) denoting the number of heads obtained in two tosses of a fair coin. Using the alternate formula for variance, we need to first calculate \(E[X^2]\), for which we use Theorem 3.6.1:
$$E[X^2] = 0^2\cdot p(0) + 1^2\cdot p(1) + 2^2\cdot p(2) = 0 + 0.5 + 1 = 1.5.\notag$$
In Example 3.6.1, we found that \(\mu = E[X] = 1\). Thus, we find
\begin{align*}
\text{Var}(X) &= E[X^2] - \mu^2 = 1.5 - 1 = 0.5 \\
\Rightarrow\ \text{SD}(X) &= \sqrt{\text{Var}(X)} = \sqrt{0.5} \approx 0.707
\end{align*}
Exercise \(\PageIndex{1}\)
Consider the context of Example 3.6.2, where we defined the random variable \(X\) to be our winnings on a single play of game involving flipping a fair coin three times. We found that \(\text{E}[X] = 1.25\). Now find the variance and standard deviation of \(X\).
- Answer
-
First, find \(\text{E}[X^2]\):
\begin{align*}
\text{E}[X^2] &= \sum_i x_i^2\cdot p(x_i) \\
&= (-1)^2\cdot\frac{1}{8} + 1^2\cdot\frac{1}{2} + 2^2\cdot\frac{1}{4} + 3^2\cdot\frac{1}{8} = \frac{11}{4} = 2.75
\end{align*} Now, we use the alternate formula for calculating variance:
\begin{align*}
\text{Var}(X) &= \text{E}[X^2] - \text{E}[X]^2 = 2.75 - 1.25^2 = 1.1875 \\
\Rightarrow \text{SD}(X) &= \sqrt{1.1875} \approx 1.0897
\end{align*}
Given that the variance of a random variable is defined to be the expected value of squared deviations from the mean, variance is not linear as expected value is. We do have the following useful property of variance though.
Theorem \(\PageIndex{2}\)
Let \(X\) be a random variable, and \(a, b\) be constants. Then the following holds:
$$\text{Var}(aX + b) = a^2\text{Var}(X).\notag$$
Exercise \(\PageIndex{2}\)
Prove Theorem 3.7.2.
- Answer
-
First, let \(\mu = \text{E}[X]\) and note that by the linearity of expectation we have
$$\text{E}[aX + b] = a\text{E}[X] + b = a\mu + b. \notag$$ Now, we use the alternate formula for variance given in Theorem 3.7.1 to prove the result:
\begin{align*}
\text{Var}(aX + b) &= \text{E}\left[(aX+b)^2\right] - \left(\text{E}[aX + b]\right)^2 \\
&= \text{E}[a^2X^2 +2abX + b^2] - \left(a\mu + b\right)^2\\
&= a^2\text{E}[X^2] + 2ab\text{E}[X] + b^2 - a^2\mu^2 - 2ab\mu - b^2 \\
&= a^2\text{E}[X^2] - a^2\mu^2 = a^2(\text{E}[X^2] - \mu^2) = a^2\text{Var}(X)
\end{align*}
Theorem 3.7.2 easily follows from a little algebraic modification. Note that the "\(+\ b\)'' disappears in the formula. There is an intuitive reason for this. Namely, the "\(+\ b\)'' corresponds to a horizontal shift of the probability mass function for the random variable. Such a transformation to this function is not going to affect the spread, i.e., the variance will not change.
As with expected values, for many of the common probability distributions, the variance is given by a parameter or a function of the parameters for the distribution.
| Distribution | Variance |
| Bernoulli(\(p\)) | \(p(1-p)\) |
| binomial(\(n, p\)) | \(np(1-p)\) |
| hypergeometric(\(N, n, m\)) | \(\frac{n(m/N)(1 - m/N)(N-n)}{N-1}\) |
| geometric(\(p\)) | \(\frac{1-p}{p^2}\) |
| negative binomial(\(r, p\)) | \(\frac{r(1-p)}{p^2}\) |
| Poisson(\(\lambda\)) | \(\lambda\) |


