4.2: Expected Value and Variance of Continuous Random Variables
- Page ID
- 3268
We now consider the expected value and variance for continuous random variables. Note that the interpretation of each is the same as in the discrete setting, but we now have a different method of calculating them in the continuous setting.
Definition \(\PageIndex{1}\)
If \(X\) is a continuous random variable with pdf \(f(x)\), then the expected value (or mean) of \(X\) is given by
$$\mu = \mu_X = \text{E}[X] = \int\limits^{\infty}_{-\infty}\! x\cdot f(x)\, dx.\notag$$
The formula for the expected value of a continuous random variable is the continuous analog of the expected value of a discrete random variable, where instead of summing over all possible values we integrate (recall Sections 3.6 & 3.7).
For the variance of a continuous random variable, the definition is the same and we can still use the alternative formula given by Theorem 3.7.1, only we now integrate to calculate the value:
$$\text{Var}(X) = \text{E}[X^2] - \mu^2 = \left(\int\limits^{\infty}_{-\infty}\! x^2\cdot f(x)\, dx\right) - \mu^2\notag$$
Example \(\PageIndex{1}\)
Consider again the context of Example 4.1.1, where we defined the continuous random variable \(X\) to denote the time a person waits for an elevator to arrive. The pdf of \(X\) was given by
$$f(x) = \left\{\begin{array}{l l}
x, & \text{for}\ 0\leq x\leq 1 \\
2-x, & \text{for}\ 1< x\leq 2 \\
0, & \text{otherwise}
\end{array}\right.\notag$$
Applying Definition 4.2.1, we compute the expected value of \(X\):
$$\text{E}[X] = \int\limits^1_0\! x\cdot x\, dx + \int\limits^2_1\! x\cdot (2-x)\, dx = \int\limits^1_0\! x^2\, dx + \int\limits^2_1\! (2x - x^2)\, dx = \frac{1}{3} + \frac{2}{3} = 1.\notag$$
Thus, we expect a person will wait 1 minute for the elevator on average. Figure 1 demonstrates the graphical representation of the expected value as the center of mass of the pdf.
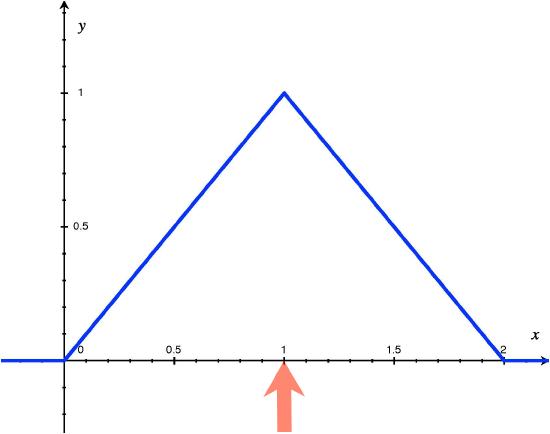
Figure 1: The red arrow represents the center of mass, or the expected value, of \(X\).
Now we calculate the variance and standard deviation of \(X\), by first finding the expected value of \(X^2\).
$$\text{E}[X^2] = \int\limits^1_0\! x^2\cdot x\, dx + \int\limits^2_1\! x^2\cdot (2-x)\, dx = \int\limits^1_0\! x^3\, dx + \int\limits^2_1\! (2x^2 - x^3)\, dx = \frac{1}{4} + \frac{11}{12} = \frac{7}{6}.\notag$$
Thus, we have
\begin{align*}
\text{Var}(X) &= \text{E}[X^2] - \mu^2 = \frac{7}{6} - 1 = \frac{1}{6} \\
\Rightarrow\ \text{SD}(X) &= \sqrt{\text{Var}(X)} = \frac{1}{\sqrt{6}} \approx 0.408
\end{align*}


