10.5: Matched or Paired Samples
- Page ID
- 6978
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When using a hypothesis test for matched or paired samples, the following characteristics should be present:
- Simple random sampling is used.
- Two measurements (samples) are drawn from the same pair of individuals or objects.
- Differences are calculated from the matched or paired samples.
- The differences form the sample that is used for the hypothesis test.
- Either the matched pairs have differences that come from a population that is normal or the number of differences is sufficiently large so that distribution of the sample mean of differences is approximately normal.
In a hypothesis test for matched or paired samples, subjects are matched in pairs and differences are calculated. The differences are the data. The population mean for the differences, \(\mu_{d}\), is then tested using a Student's \(t\)-test for a single population mean with \(n - 1\) degrees of freedom, where \(n\) is the number of differences.
The test statistic (\(t\)-score) is:
\[t = \dfrac{\bar{x}_{d} - \mu_{d}}{\left(\dfrac{s_{d}}{\sqrt{n}}\right)}\]
Example \(\PageIndex{1}\)
A study was conducted to investigate the effectiveness of hypnotism in reducing pain. Results for randomly selected subjects are shown in Table. A lower score indicates less pain. The "before" value is matched to an "after" value and the differences are calculated. The differences have a normal distribution. Are the sensory measurements, on average, lower after hypnotism? Test at a 5% significance level.
| Subject: | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Before | 6.6 | 6.5 | 9.0 | 10.3 | 11.3 | 8.1 | 6.3 | 11.6 |
| After | 6.8 | 2.4 | 7.4 | 8.5 | 8.1 | 6.1 | 3.4 | 2.0 |
Answer
Corresponding "before" and "after" values form matched pairs. (Calculate "after" – "before.")
| After Data | Before Data | Difference |
|---|---|---|
| 6.8 | 6.6 | 0.2 |
| 2.4 | 6.5 | -4.1 |
| 7.4 | 9 | -1.6 |
| 8.5 | 10.3 | -1.8 |
| 8.1 | 11.3 | -3.2 |
| 6.1 | 8.1 | -2 |
| 3.4 | 6.3 | -2.9 |
| 2 | 11.6 | -9.6 |
The data for the test are the differences: \(\{0.2, -4.1, -1.6, -1.8, -3.2, -2, -2.9, -9.6\}\)
The sample mean and sample standard deviation of the differences are: \(\bar{x}_{d} = -3.13\) and \(s_{d} = 2.91\) Verify these values.
Let \(\mu_{d}\) be the population mean for the differences. We use the subscript dd to denote "differences."
Random variable:
\(\bar{X}_{d} =\) the mean difference of the sensory measurements
\[H_{0}: \mu_{d} = 0\]
The null hypothesis is zero, meaning that there is the same pain felt after hypnotism. That means the subject shows no improvement. \(\mu_{d}\) is the population mean of the differences.
\[H_{a}: \mu_{d} < 0\]
The alternative hypothesis is negative, meaning there is less pain felt after hypnotism. That means the subject shows improvement. The score should be lower after hypnotism, so the difference ought to be negative to indicate improvement.
Distribution for the test:
The distribution is a Student's t with \(df = n - 1 = 8 - 1 = 7\). Use \(t_{7}\). (Notice that the test is for a single population mean.)
Calculate the p-value using the Student's-t distribution:
\[p\text{-value} = 0.0095\]
Graph:
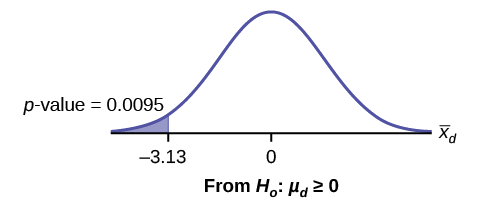
\(\bar{X}_{d}\) is the random variable for the differences.
The sample mean and sample standard deviation of the differences are:
\(\bar{x}_{d} = -3.13\)
\(s_{d} = 2.91\)
Compare \(\alpha\) and the \(p\text{-value}\)
\(\alpha = 0.05\) and \(p\text{-value} = 0.0095\). \(\alpha > p\text{-value}\)
Make a decision
Since \(\alpha > p\text{-value}\), reject \(H_{0}\). This means that \(\mu_{d} < 0\) and there is improvement.
Conclusion
At a 5% level of significance, from the sample data, there is sufficient evidence to conclude that the sensory measurements, on average, are lower after hypnotism. Hypnotism appears to be effective in reducing pain.
For the TI-83+ and TI-84 calculators, you can either calculate the differences ahead of time (after - before) and put the differences into a list or you can put the after data into a first list and the before data into a second list. Then go to a third list and arrow up to the name. Enter 1st list name - 2nd list name. The calculator will do the subtraction, and you will have the differences in the third list.
Use your list of differences as the data. Press STAT and arrow over to TESTS. Press 2:T-Test. Arrow over to Data and press ENTER. Arrow down and enter 0 for \(\mu_{0}\), the name of the list where you put the data, and 1 for Freq:. Arrow down to \(\mu\): and arrow over to < \(\mu_{0}\). Press ENTER. Arrow down to Calculate and press ENTER. The \(p\text{-value}\) is 0.0094, and the test statistic is -3.04. Do these instructions again except, arrow to Draw (instead of Calculate). Press ENTER.
Two dependent Samples with data Calculator
Type in the values from the two data sets separated by commas, for example, 2,4,5,8,11,2. Then enter the tail type and the confidence level and hit Calculate and the test statistic, t, the p-value, p, the confidence interval's lower bound, LB, the upper bound, UB, and the data set of the differences will be shown. Be sure to enter the confidence level as a decimal, e.g., 95% has a CL of 0.95.
Data1:
Data2:
|
CL: |
| t: | p | LB | UB |
DataDiff:
Exercise \(\PageIndex{1}\)
A study was conducted to investigate how effective a new diet was in lowering cholesterol. Results for the randomly selected subjects are shown in the table. The differences have a normal distribution. Are the subjects’ cholesterol levels lower on average after the diet? Test at the 5% level.
| Subject | A | B | C | D | E | F | G | H | I |
|---|---|---|---|---|---|---|---|---|---|
| Before | 209 | 210 | 205 | 198 | 216 | 217 | 238 | 240 | 222 |
| After | 199 | 207 | 189 | 209 | 217 | 202 | 211 | 223 | 201 |
Answer
The \(p\text{-value}\) is 0.0130, so we can reject the null hypothesis. There is enough evidence to suggest that the diet lowers cholesterol.
Example \(\PageIndex{2}\)
A college football coach was interested in whether the college's strength development class increased his players' maximum lift (in pounds) on the bench press exercise. He asked four of his players to participate in a study. The amount of weight they could each lift was recorded before they took the strength development class. After completing the class, the amount of weight they could each lift was again measured. The data are as follows:
| Weight (in pounds) | Player 1 | Player 2 | Player 3 | Player 4 |
|---|---|---|---|---|
| Amount of weight lifted prior to the class | 205 | 241 | 338 | 368 |
| Amount of weight lifted after the class | 295 | 252 | 330 | 360 |
The coach wants to know if the strength development class makes his players stronger, on average.
Record the differences data. Calculate the differences by subtracting the amount of weight lifted prior to the class from the weight lifted after completing the class. The data for the differences are: \(\{90, 11, -8, -8\}\). Assume the differences have a normal distribution.Using the differences data, calculate the sample mean and the sample standard deviation.
\[\bar{x}_{d} = 21.3\]
and
\[s_{d} = 46.7\]
The data given here would indicate that the distribution is actually right-skewed. The difference 90 may be an extreme outlier? It is pulling the sample mean to be 21.3 (positive). The means of the other three data values are actually negative.
Using the difference data, this becomes a test of a single __________ (fill in the blank).
Define the random variable: \(\bar{X}\) mean difference in the maximum lift per player.
The distribution for the hypothesis test is \(t_{3}\).
- \(H_{0}: \mu_{d} = 0\),
- \(H_{a}: \mu_{d} > 0\)
Graph:
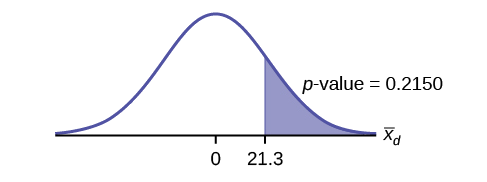
Calculate the \(p\text{-value}\): The \(p\text{-value}\) is 0.2150
Decision: If the level of significance is 5%, the decision is not to reject the null hypothesis, because \(\alpha < p\text{-value}\).
What is the conclusion?
At a 5% level of significance, from the sample data, there is not sufficient evidence to conclude that the strength development class helped to make the players stronger, on average.
Exercise \(\PageIndex{2}\)
A new prep class was designed to improve SAT test scores. Five students were selected at random. Their scores on two practice exams were recorded, one before the class and one after. The data recorded in Table. Are the scores, on average, higher after the class? Test at a 5% level.
| SAT Scores | Student 1 | Student 2 | Student 3 | Student 4 |
|---|---|---|---|---|
| Score before class | 1840 | 1960 | 1920 | 2150 |
| Score after class | 1920 | 2160 | 2200 | 2100 |
Answer
The \(p\text{-value}\) is 0.0874, so we decline to reject the null hypothesis. The data do not support that the class improves SAT scores significantly.
Example \(\PageIndex{3}\)
Seven eighth graders at Kennedy Middle School measured how far they could push the shot-put with their dominant (writing) hand and their weaker (non-writing) hand. They thought that they could push equal distances with either hand. The data were collected and recorded in Table.
| Distance (in feet) using | Student 1 | Student 2 | Student 3 | Student 4 | Student 5 | Student 6 | Student 7 |
|---|---|---|---|---|---|---|---|
| Dominant Hand | 30 | 26 | 34 | 17 | 19 | 26 | 20 |
| Weaker Hand | 28 | 14 | 27 | 18 | 17 | 26 | 16 |
Conduct a hypothesis test to determine whether the mean difference in distances between the children’s dominant versus weaker hands is significant.
Record the differences data. Calculate the differences by subtracting the distances with the weaker hand from the distances with the dominant hand. The data for the differences are: \(\{2, 12, 7, –1, 2, 0, 4\}\). The differences have a normal distribution.
Using the differences data, calculate the sample mean and the sample standard deviation. \(\bar{x} = 3.71\), \(s_{d} = 4.5\).
Random variable: \(\bar{X} =\) mean difference in the distances between the hands.
Distribution for the hypothesis test: \(t_{6}\)
\(H_{0}: \mu_{d} = 0 H_{a}: \mu_{d} \neq 0\)
Graph:
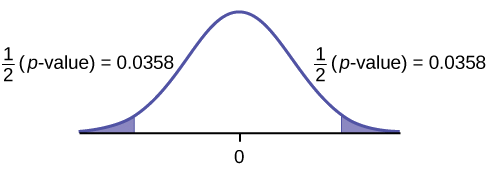
Calculate the p-value: The \(p\text{-value}\) is 0.0716 (using the data directly).
(test statistic = 2.18. \(p\text{-value} = 0.0719\) using \((\bar{x}_{d} = 3.71, s_{d} = 4.5\).
Decision: Assume \(\alpha = 0.05\). Since \(\alpha < p\text{-value}\), Do not reject \(H_{0}\).
Conclusion: At the 5% level of significance, from the sample data, there is not sufficient evidence to conclude that there is a difference in the children’s weaker and dominant hands to push the shot-put.
Exercise \(\PageIndex{3}\)
Five ball players think they can throw the same distance with their dominant hand (throwing) and off-hand (catching hand). The data were collected and recorded in Table. Conduct a hypothesis test to determine whether the mean difference in distances between the dominant and off-hand is significant. Test at the 5% level.
| Player 1 | Player 2 | Player 3 | Player 4 | Player 5 | |
|---|---|---|---|---|---|
| Dominant Hand | 120 | 111 | 135 | 140 | 125 |
| Off-hand | 105 | 109 | 98 | 111 | 99 |
Answer
The \(p\text{-level}\) is 0.0230, so we can reject the null hypothesis. The data show that the players do not throw the same distance with their off-hands as they do with their dominant hands.
Confidence Intervals for the Difference Between Two Population Means (Dependent Samples)
As we have seen repeatedly, if we can perform a hypothesis test, then a confidence interval can also be constructed. This is still the case for paired data. The formula is similar to the confidence interval for a single population mean.
Formula for the Confidence Interval for Paired Data
\((\bar{x}_d - z_{\dfrac{\alpha}{2}} \dfrac{s_{d}}{\sqrt{n}}, \bar{x}_d + z_{\dfrac{\alpha}{2}} \dfrac{s_{d}}{\sqrt{n}})\)
Everyone uses technology to perform the calculations. If you use the TI calculator, enter in the data just as is done for hypothesis tests, but go to TInterval and make sure you choose the list of differences. It is easiest to use the built in calculator above in this section or use another online calculator.
Example \(\PageIndex{4}\)
A company that sells snowboards wants to see how much sales increase when it posts advertisements on Google. The company kept track of the number of snowboards sold online during of the first eight days in December last year when there were no Google ads posted and the first eight days in December this year when the Google ads were posted. The table below shows the sales data.
| Dec 1 | Dec 2 | Dec 3 | Dec 4 | Dec 5 | Dec 6 | Dec 7 | Dec 8 | |
|---|---|---|---|---|---|---|---|---|
| No Ads | 37 | 32 | 41 | 26 | 30 | 54 | 22 | 19 |
| With Ads | 63 | 98 | 103 | 75 | 88 | 130 | 99 | 65 |
Find and interpret the 95% confidence interval for the difference.
Calculate the confidence interval using technology: (-71.6737, -43.3263) or (-72,-43) rounded to the nearest whole number.
Interpret the lower bound: Since it is negative, this means that sales with ads are likely to be higher than without ads. In particular, it is likely that the population mean number of snowboard daily sales has increased no more than 73 per day now that ads are posted on Google.
Interpret the upper bound: Since it is negative, this means that sales with ads are still likely to be higher than without ads. In particular, it is likely that the population mean number of snowboard daily sales has increased by at least 43 per day now that ads are posted on Google.
Putting it Together: With 95% confidence the sales manager can conclude that the population mean number of snowboard daily sales has increased by between 43 per day and 72 per day now that ads are posted on Google.
Assumptions: We must assume that the first eight days of December are an unbiased sample. Also, since the sample size of 8 is not greater than 30, we must assume that the distribution of differences in sales by date is approximately normal. This assumption has no reason for being true, hence increasing the sample size to over 30 is highly recommended.
Uses: A manager would calculate the increased profit by multiplying 43 and 73 by the profit per snowboard sale and compare these to the daily advertising cost that Google charges to make a decision about whether the advertising was successful.
Exercise \(\PageIndex{4}\)
Nine American voters were asked how old is too old to be a member of Congress and how old is told to be the president of the United States. The table below shows the results of the survey.
| Voter 1 | Voter 2 | Voter 3 | Voter 4 | Voter 5 | Voter 6 | Voter 7 | Voter 8 | Voter 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Congress | 80 | 75 | 65 | 80 | 78 | 70 | 75 | 85 | 69 |
| President | 65 | 70 | 70 | 75 | 67 | 65 | 73 | 80 | 75 |
Find and interpret the 95% confidence interval for the difference.
Answer
The 95% confidence interval is (-1.0373,9.260) or (-1,9) rounded to the nearest whole number. It is likely that the population mean age that voters think is too old to be in Congress is no more than 1 year younger the age that they think is too old to be the president of the United States. It is also likely that the population mean age that voters think is too old to be in Congress is no more than 9 years older the age that they think is too old to be the president of the United States. In other words, with 95% confidence, the population mean age that voters think is too old to be in Congress is between 1 year younger and 9 years older than the age that they think is too old to be the president of the United States. We must assume that the sampling technique was simple random sampling and since 9 < 31, we must assume that the distribution of differences is approximately normal.
Chapter Review
A hypothesis test for matched or paired samples (\(t\)-test) has these characteristics:
- Test the differences by subtracting one measurement from the other measurement
- Random Variable: \(x_{d} =\) mean of the differences
- Distribution: Student’s-t distribution with \(n - 1\) degrees of freedom
- If the number of differences is small (less than 30), the differences must follow a normal distribution.
- Two samples are drawn from the same set of objects.
- Samples are dependent.
Formula Review
Test Statistic (t-score): \[t = \dfrac{\bar{x}_{d}}{\left(\dfrac{s_{d}}{\sqrt{n}}\right)}\]
where:
\(x_{d}\) is the mean of the sample differences. \(\mu_{d}\) is the mean of the population differences. \(s_{d}\) is the sample standard deviation of the differences. \(n\) is the sample size.
Contributors
Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/30189442-699...b91b9de@18.114.


