The Z-score
- Page ID
- 221
The Standard Normal Distribution
The Standard Normal distribution follows a normal distribution and has mean of 0 and standard deviation of 1.

Notice that the Standard Normal distribution is perfectly symmetric about 0. If a distribution is normal, but not standard, we can convert a value to the Standard normal distribution table by first by finding how many standard deviations away the number is from the mean.
The z-score
The number of standard deviations from the mean is called the z-score and can be found by the formula
\[ z = \dfrac {x-m}{\sigma} \label{zscore} \]
Find the z-score corresponding to a raw score of 132 from a normal distribution with mean 100 and standard deviation 15.
Solution
Using Equation \ref{zscore}, we compute
\[ x = \dfrac{132 - 100}{15} = 2.133 \nonumber \]
A z-score of 1.7 was found from an observation coming from a normal distribution with mean 14 and standard deviation 3. Find the raw score.
Solution
Plugging these into Equation \ref{zscore}, we have
\[ 1.7 = \dfrac{x-14}{3} \nonumber \]
To solve this we just multiply both sides by the denominator 3,
\[ \begin{align*} (1.7)(3) &= x - 14 \\[4pt] 5.1 &= x - 14 \\[4pt] x &= 19.1 \end{align*} \]
The z-score and Area
Often we want to find the probability that a z-score will be less than a given value, greater than a given value, or in between two values. To accomplish this, we use the table from the textbook and a few properties about the normal distribution.
Find
\[ P(z < 2.37) \nonumber \]
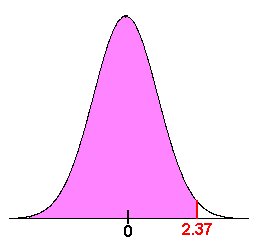
Solution
We use the table. Notice the picture on the table has shaded region corresponding to the area to the left (below) a z-score. This is exactly what we want. Below are a few lines of the table.
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
The columns corresponds to the ones and tenths digits of the z-score and the rows correspond to the hundredths digits. For our problem we want the row 2.3 (from 2.37) and the row .07 (from 2.37). The number in the table that matches this is 0.9911. Hence
\[ P(z < 2.37) = 0.9911 \nonumber \]
Find
\[ P(z > 1.82) \nonumber \]
Solution
In this case, we want the area to the right of 1.82.
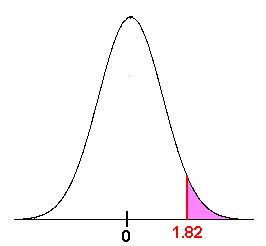
This is not what is given in the table. We can use the identity
\[ P(z > 1.82) = 1 - P(z < 1.82) \nonumber \]
reading the table gives
\[ P(z < 1.82) = 0.9656 \nonumber \]
Our answer is
\[ P(z > 1.82) = 1 - .9656 = 0.0344 \nonumber \]
Find
\[ P(-1.18 < z < 2.1) \nonumber \]
Solution
Once again, the table does not exactly handle this type of area.
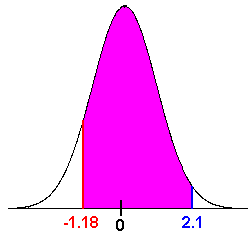
However, the area between -1.18 and 2.1 is equal to the area to the left of 2.1 minus the area to the left of -1.18. That is
\[ P(-1.18 < z < 2.1) = P(z < 2.1) - P(z < -1.18) \nonumber \]
To find \(P(z < 2.1)\) we rewrite it as \(P(z < 2.10)\) and use the table to get
\[ P(z < 2.10) = 0.9821. \nonumber \]
The table also tells us that
\[ P(z < -1.18) = 0.1190 \nonumber \]
Now subtract to get
\[ P(-1.18 < z < 2.1) = 0.9821 - 0.1190 = 0.8631 \nonumber \]


